На форуме физфака МГУ
http://forum.dubinushka.ru/index.php?s= ... topic=4122 у меня возникли разногласия по основополагающему принципу, на котором строится квантовая механика, т.е. по принципу наименьшего действия (ПНД), который Планк использовал для обоснования своих квантов действия на заре КМ, а позже Фейнман для новой интерпретации квантовой механики. Я провел несколько вычислительных экспериментов на математической модели простейшей системы, а конкретно рассмотрел движение снаряда в поле тяжести Земли (для проверки релятивистской формы ПНД) и движение заряженного снаряда в электростатическом поле заряда той же величины и обратного знака (вид поля будет тот же) для проверки классической формы ПНД во второй редакции ПНД, т.е. редакции Гамильтона-Остроградского (первую редакцию использовали Эйлер и Лагранж) и у меня получились результаты, которые опровергают этот принцип. Но два моих оппонента seggah и Max Sukharev заявили, что они независимо друг от друга тоже провели такие же вычислительные эксперименты (правда сами уравнения описывающие движения снаряда в поле тяжести Земли один списал у другого, т.к. сам наверное не смог смоделировать движение снаряда) и у них получились данные, которые противоречат моим, т.е. подтверждают справедливость ПНД. Правда, быстрее всего Max Sukharev вообще ничего не проверял, а просто поддержал того, кто был против меня. Такой вывод можно сделать после реплики одного из моих оппонентов (Munin) в адрес другого моего оппонента (Owen) “Странно слышать это от человека, который защищает ПНД, в адрес челвоека, который защищает ПНД.”, т.е. большинству моих оппонентов на этом форуме важно было не разобраться в моем сообщение, которое им очень не понравилось, а просто закопать меня во что бы то ни стало. В связи с этим возникла тупиковая ситуация и я решил обратиться за помощью для проведения так сказать независимой экспертизы. По этому я прошу всех, кто может мне в этом помочь проверить полученные мною результаты.
Коротко напомню этот принцип, согласно которому утверждается, что при свободном движение любого тела в каком то поле (гравитационном или электростатическом), т.е. если на него не будут действовать больше никакие силы, то величина, называемая действием, будет иметь минимальное значение по сравнению с действием полученным при движение по любому другому пути, когда тело будет двигаться по какой то направляющей (можно сказать имеется уравнение удерживающей связи) или на тело будут действовать еще какие то силы (кроме сил притяжения создаваемых этим полем). При этом сравниваемые движения должны начинаться и кончаться в одних и тех же точках и время движения от начальной точки до конечной должно быть одно и тоже. Действие вычисляется, как интеграл по времени движения от лагранжиана

, т.е. разности кинетической и потенциальной энергии движущегося тела. Кинетическая энергия вычисляется как

, где

это масса тела, а

его скорость. А вот потенциальную энергию вычисляют по разному, хотя по одной и той же формуле, например, для гравитационного поля

, а для электростатического поля

, где

- это расстояние от снаряда до центра притяжения (центра Земли или второго неподвижного заряда), но численные значения действия будут разные если взять разные

. И я на всякий случай подсчитал действие не только, когда за нулевой уровень потенциальной энергии принята поверхность сферы, центр которой совпадает с центром второго тела (центра притяжения), а радиус

принят произвольно (действие будет Sser), но и по формуле, когда за нулевой уровень потенциальной энергии принято расстояние до сферы, когда

равно бесконечности (действие будет Sseg).
Начнем с классической формы. Для этого посмотрите на левый рисунок (двойного рисунка), где показаны различные траектории движения (сразу извиняюсь за выбор начала координат, что диктуется особенностями примененной для решения уравнений программы), а в таблице я привел полученные при этом значения действия, из которых следует, что на свободном пути действие не будет ни только минимальным, но и максимальным. При этом я рассмотрел движение не в гравитационном поле, а поле сил Кулона от взаимодействия двух разноименно заряженных зарядов

=0,0005 к только для того, чтобы расстояния и время движения были более привычны для восприятия. Неподвижный заряд располагается в точке с координатами

=0,

=-10 м, а первый заряд с массой

=1 кг (

тоже можно принять равной 1 кг) вылетает из точки А с координатами

=-50 м,

=0 м и движется в точку В с координатами

=18 м,

=-0,01 м (

принято не равным нулю только вследствие особенностей программы Hrono1). Свободное движение это коричневая кривая, а не свободное, т.е. по направляющим, а конкретно по прямой (сиреневая линия) и дугам окружности с разными радиусами и соответствующими им координатами центра окружности

(всегда равно -16 м) и

(красные кривые). Данные о начальных скоростях движения

,

(м/с), времени движения

(с) и полученном при этом действии S (Дж*с) я также даю в виде таблицы. При этом для вычисления Sser принято

=10 м.

№____траектория_____VX_____VY______t______Sser_______Sseg_____R40_____Y40
1_____свободное______10_____- 6____4,89____213,4_____1313____------____------
2_____прямая________9,15_____0_____4,89___- 72,2_____1028____------____------
3____дуга окружн_____0,42___20,95___4,89____307,4_____1407____34,01___-0,68
4____дуга окружн_____3,66___18,27___4,89____131,8_____1232____34,67___- 6,81
5____дуга окружн_____9,99___4,99____4,89___- 142,6____957,7____76,03___- 68,01
6____дуга окружн_____5,17__- 12,92___4,89____261,4_____1362____36,62___13,60
7____дуга окружн_____3,25__- 16,27___4,89____329,5_____1429____34,67____6,79
Более того на правом рисунке (двойного рисунка) я привожу несколько примеров свободного движения из точки А в точку В такого же заряда, но движущегося в мультиполе, т.е. в суммарном поле от действия двух неподвижных зарядов и одного не свободного движения по дуге окружности (красная кривая). Как видно из рисунка, при движение из одной точки в другую в мультиполях возможно несколько свободных (истинных) движений, что противоречит ПНД и делает не возможным провести сравнение величин действия при свободном и не свободном движение, т.к. не понятно с каким свободным движением сравнивать не свободные. Можно было бы привести еще рисунок, где в таком же поле я получил две свободные траектории, когда и время движения одно и то же и начальная скорость одна и та же, т.е. выполнены требования ПНД как в первой редакции, так и во второй, и кому это интересно могут посмотреть это в моей статье «О принципах кратчайшего времени и наименьшего действия». А для тех у кого есть затруднения с моделированием движения снаряда могут привести некоторые уравнения для описания этого движения в декартовой системе координат, где основными являются уравнения для определения ускорений

и

по осям

и

при воздействие на тело сил

и

, которые вычисляются как проекции на оси

и

суммарной силы притяжения
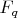
(в электростатическом поле) или

(в гравитационном поле). Для решения системы дифференциальных уравнений я применял один из методов численного решения дифференциальных уравнений, а конкретно метод Рунге-Кутта по четырем коэффициентам. Если движение будет осуществляться по направляющим, то при вычисление сил

и

надо будет учесть еще реакцию со стороны напрвляющей, но в приведенных ниже уравнениях для простоты не учтены силы упругости при деформации направляющей и силы жидкостного трения возникающие в материале направляющей при ее деформации, которые позволяют сгладить процесс численного решения уравнений, т.е. погасить колебания возникающие при не очень точном задании начальных условий или большом шаге решения, но Вы их всегда можно туда добавить при необходимости.
При этом действие S будет вычисляться, как сумма элементарных действий на каждом шаге решения

, где

шаг решения в секундах. В рассмотренных задачах принято: радиус Земли 6378 км, масса Земли

кг, гравитационная постоянная

, масса снаряда

=1 кг, а коэффициент в формуле Кулона

. Если кто то надумает повторить эти эксперименты на программе Hrono1, то могу сообщить, что шаг решения был 0,01 с, жесткость направляющей

=1000 н/м, а коэффициент жидкостного трения в материале направляющей был

=10 н*с/м (если жесткость напрвляющей будет меньше, то отклонение при движение от направляющей будет больше). При этом не забудьте при движение по дуге поставить две галочки у надписи “дуга”. Ниже привожу кусок кода программы с двумя дифференциальными уравнениями описывающими движение снаряда, чтобы не подумали, что в программе есть какие то фокусы с зайцами в рукавах.
Код:
R = SQR(X^2 + (Y + R0ser)^2)
Fq = - Kq * q1 * q2 / R^2
Fm = gamma * m1 * m2 / R^2
alfa = ABS(ARCTAN((Y +R0ser) / X))
FX = - (Fm + Fq) * COS(alfa): IF X < 0 THEN FX = -FX
FY = - (Fm + Fq) * SIN(alfa): IF Y+R0ser < 0 THEN FY = -FY
wX = FX / m1
wY = FY / m1
Для проверки ПНД в релятивистской форме, когда на свободном (истинном) пути будет не только действие минимально, но и суммарное замедление времени от действия скоростного фактора и гравитационного тоже будет минимально (или ускорение времени максимально), я рассматриваю задачу Фейнмана, который утверждает, что если в течение 1 часа в поле тяготения Земли ракета (неуправляемая) или просто снаряд будет лететь по свободному пути, то замедление времени будет минимальным по сравнению с любым не свободным путем, т.е. когда у нас будет управляемая ракета, которая будет по какой то программе изменять свою скорость полета и высоту, что равносильно движению по какой то направляющей, когда у нас будет уравнение удерживающей связи. Я немного усложнил задачу Фейнмана и посчитал 2-а варианта для 1-часа и для 2-часов (схема полета дана на одиночном рисунке). На рисунке изображены траектории полета из точки А в точку В при свободном движение (верхние кривые) и при не свободном движение, где в качестве примера я взял движение по одной и той же дуге окружности и для 1 часа и для 2 часов полета, нижняя кривая (дуга).
Если координаты центра Земли будут

=0 и

= -6378 км, то при времени движения 1 час (точнее 3645 сек) из точки А с координатами

= -6378 км и

= -6378 км в точку В с координатами

= 6165 км и

= -8000 км при свободном движение (по эллипсу) и при начальной скорости ракеты (снаряда)

-1460 м/с и

8000 м/с у меня получилось действие Sser= 56,8*10^9 Дж*с при

(S1seg=284,6) и ускорение времени

= 3,55-9,86= - 6,32 *10^-7 с, а при не свободном движение (по дуге окружности) и при начальной скорости

-1214 м/с и

-6589 м/с у меня действие получилось S1ser= 35,1*10^9 Дж*с (S1seg=262,9), а ускорение времени

=2,6-6,51= - 3,91 *10^-7 с. При этом радиус дуги окружности был

6333 км и координаты центра окружности

-150 км и

-7525 км. А если взять время движения 2 часа (точнее 7220 сек) из точки А с координатами

-6378 км и

-6378 км в точку В с координатами

6215 км и

-8000 км то при свободном движение (по эллипсу) у меня получился обратный результат, но наверное можно подобрать траекторию, когда и в этом случае ПНД в релятивистской форме будет нарушаться. Впрочем, это уже не имеет никакого значения, т.к. если ПНД нарушается в первом примере при времени движения 1 час, что соответствует задаче Фейнмана, то это уже не принцип. Данные по этим экспериментам я также представляю в виде таблицы, где ttR убыстрение времени от уменьшения гравитации согласно общей теории относительности и ttV замедление времени от действия скорости согласно преобразованиям Лоренца, которые я вычислял по ниженриведенным формулам, где

2.998 * 10 ^ 8 м/с.
Код:
ttR=ttR+h*gamma*m2*(1/Rземли-1/R)/Vsv^2
ttV=ttV+h*(1-1/SQR(1-V^2/Vsv^2))
Если кто то надумает повторить и эти эксперименты на программе Hrono1, то могу сообщить, что шаг решения был при свободном движение 1 с, а при вынужденном 0,5 с, жесткость направляющей

10 н/м, а коэффициент жидкостного трения в материале направляющей был

0,1 н*с/м. При этом, как и в первом случае, не забудьте при движение по дуге поставить две галочки у надписи “дуга”.

№__траектория______VX_____VY_____t_____Sser___Sseg____ttR_____ttV_____tt
1_свободное_1час__- 1460___8000__3645___56,8___284,6___3,55___- 9,86__- 6,32
2_дуга_окр__1час__- 1214__- 6589__3645___35,1___262,9___2,60___- 6,51__- 3,91
3_свободное_2час__- 3820___8170__7220___- 76,4__374,8___20,58__- 12,08__8,5
4_дуга окр__2час___-1070__- 4961__7220___- 28,8__425,0___6,61___- 3,74___2,85
Таким образом, полученные экспериментальные данные, полностью опровергают наличие в Природе ПНД, как в классической форме, так и в релятивистской, но меня сейчас интересует не это, а то насколько я грамотно провел вычислительные эксперименты на математических моделях систем. По этому у меня будет большая просьба ко всем, кого заинтересовали полученные мною данные, выполнить эти вычислительные эксперименты самостоятельно и сообщить мне о полученных результатах. Если кого то заинтересуют подробности, то можете скачать мои статьи и программы с моей домашней страницы или ее зеркала.
С наилучшими пожеланиями Сергей Юдин.