1. Ваши слова
Цитата:
...

,

- независимые переменные. ...
излишни, поскольку совместная плотность распределения

факторизуется в виде произведения

, где функция

,
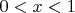
, зависит лишь от переменной

, а функция

,

– лишь от переменной

. Такая факторизация равносильна независимости

и

.
2. Прямой способ найти плотность случайной величины

по совместной плотности

(неважно, зависимых или независимых величин

) – использовать

-функцию Дирака:

В Вашем случае имеем
![\begin{multline*}f_{XY}(z)=\int_1^\infty \int_0^1\delta(z-xy) \frac{4x}{y^3} \textrm{d}x \textrm{d}y \stackrel{t=xy}{=} \int_1^\infty \int_0^y\delta(z-t) \frac{4t}{y^5} \textrm{d}t \textrm{d}y= 4z \theta(z)\int_1^\infty \theta(y-z) y^{-5} \textrm{d}y=\\= 4z \theta(z)\int_{\max(z,1)}^\infty y^{-5} \textrm{d}y = \theta(z)\frac{z}{\max^4(z,1)}\equiv\begin{cases}0, & z<0,\\ z, & z\in [0;\,1],\\ 1/z^3 & z>1. \end{cases}\end{multline*} \begin{multline*}f_{XY}(z)=\int_1^\infty \int_0^1\delta(z-xy) \frac{4x}{y^3} \textrm{d}x \textrm{d}y \stackrel{t=xy}{=} \int_1^\infty \int_0^y\delta(z-t) \frac{4t}{y^5} \textrm{d}t \textrm{d}y= 4z \theta(z)\int_1^\infty \theta(y-z) y^{-5} \textrm{d}y=\\= 4z \theta(z)\int_{\max(z,1)}^\infty y^{-5} \textrm{d}y = \theta(z)\frac{z}{\max^4(z,1)}\equiv\begin{cases}0, & z<0,\\ z, & z\in [0;\,1],\\ 1/z^3 & z>1. \end{cases}\end{multline*}](https://dxdy-02.korotkov.co.uk/f/d/d/8/dd8ff8d0573f5073c28e994ed122f61282.png)
Здесь

- функция Хевисайда. Она, также как и символ

, использовалась лишь для того, чтобы "укомпактить" разбор разных случаев.



