Считаю я интеграл следующего вида по области D, образованной кольцевыми поверхностями с радиусами r и R:

.
Далее я буду считать только первый интеграл, т.к. второй будет такой же, с разницей лишь в букве r. И да, здесь я как бы вынес за знак интеграла давление и коэффициент трения.
Далее переходим к полярным координатам:
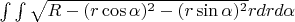
Получается:

С пределами интегрирования:

Далее для решения r заносим под знак дифференциала. В итоге получаем ответ для уменьшаемого:

Если берем еще интеграл вычитаемого, который будет считаться также с точностью до буквы и вытчем, то получим следующее:

Далее припишем сюда давление и коэеффициент трения, которые я вынес вначале из под знака интеграла:

, что немного отличается, от того, что должно получится для момента сил трения кольцевых поверхностей:

или

То есть по сути, отличие только в дробности показателей степеней.
Буду вам благодарен, если поможете найти ошибку или объясните, что я делаю не так.



