Задача решается, если разность двух каких-нибудь корней равна квадрату числа в поле, которому принадлежат сами корни. Иначе преобразование получается нерациональным.
Не добившись от задачи согласия, я её испытал на примере.
Итак, попробую ещё раз объяснить.
Пусть, линейной заменой

любую кривую

можно привести к виду

где

Возьмём кривую

Которая получается из верхней кривой при

тогда
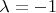
И мы должны с помощью преобразований получить такую кривую

Поскольку число

конгруэнтно, то первая кривая
имеет бесконечно много рациональных точек.
Во второй кривой число

не конгруэнтно и, следовательно, кривая
не имеет рациональных точек кроме трёх тривиальных.
А это очень неправильно, если преобразования изначально были рациональны. Значит, где-то у меня ошибка.



