Таким образом, задача ТС столь же сложна (или столь же проста, это смотря с какой стороны посмотреть), как и теорема Ферма-Эйлера.
Абсолютно одно и то же.
да я уже натыкалась на такую идею решения, но врядли на олимпиаде за 10 клас хотели увидеть доказательство теорема Ферма-Эйлер о двух квадратах.
И не увидите, оно занимает несколько страниц. Структура примерно такая:
1) если какая-то сумма квадратов делится на сумму квадратов, то и частное тоже сумма квадратов;
2) если сумма квадратов делится на какое-то число, то это число - сумма квадратов;
3) для всякого простого
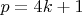
найдётся сумма квадратов которая делится на

.
Первые два доказываются методом бесконечного спуска, а вот доказательства третьего методом бесконечного спуска сколько я ни искал (ни сам, ни в книжках, ни в интернете) так и не нашёл.
А если методом Лагранжа, то десятиклассникам такое и не снилось.