======= 140 ========Задача ММ140 навеяна
вот этой.
ММ140 (10 баллов)
На квадратной площади, разлинованной на

клеток (полей) собрались

человек, каждый из которых является либо рыцарем (всегда говорят правду), либо лжецом (всегда лгут). Каждый расположился на отдельном поле. После этого каждый произнес: "Среди моих соседей поровну рыцарей и лжецов". Какова наибольшая возможная доля рыцарей среди собравшихся?
Примечания:

;
Соседними считаются поля, имеющие общую сторону;
Каждый из собравшихся знает, кем являются его соседи.
===============РешениеСразу заметим, что в крайних линиях (горизонталях и вертикалях) могут стоять только лжецы: если поле не угловое, то у него нечетное число соседей; оба соседа человека, занимающего угловое поле лжецы, следовательно он сам тоже лжец.
У каждого рыцаря ровно два соседа лжецы. При этом один лжец может соседствовать максимум четырем рыцарям. Если бы это было верно для всех лжецов, доля рыцарей получилась бы

. Но по краям площади стоят лжецы, поэтому значение

не достижимо (хотя легко достигается на бесконечной площади).
Покажем, что доля рыцарей может превышать любое число, меньшее

.
Из многочисленных конфигураций, приводящих к решению, я воспользуюсь одной из предложенных Сергеем Половинкиным (она наиболее плотная из всех и достижение долей рыцарей достаточно близких к

не требует триллионных значений

).
Регулярный (повторяющийся) элемент заполнения этой конфигурации можно увидеть на следующем рисунке:

А вот как можно выйти на такое заполнение, если стартовать с краев площади:

Доля рыцарей на регулярном участке заполнения равна

.
Ясно, что на краях и в слоях, близких к краям площади, плотность рыцарей меньше. Но с ростом n число клеток в крайних слоях растет линейно, а число клеток во внутренней области квадратично. Поэтому, используя приведенную схему заполнения можно получить долю рыцарей, сколь угодно близкую к

.
Но нас интересует не

, а

! Поэтому увеличим сторону квадрата, составляющего регулярный участок заполнения внутренней области.
На следующем рисунке представлен участок заполнения, на котором хорошо видны такие квадраты.

А вот как будет выглядеть четвертинка (остальные четверти можно получить зеркальными отражениями) площади 327х327, заполненной подобным образом.

Доля рыцарей на регулярном участке уже

. Теперь, увеличивая

, можно сколь угодно приблизиться к

.
В частности, для площади 327х327 превышает
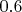
(327 - это наименьшее n, для которого мне это удалось).
Доля рыцарей на регулярном квадратном участке меньше

, за счет "лагун" из лжецов в узлах решетки, образующейся при регулярном заполнении площади, а также на границах, разделяющих квадратные участки. Но размер лагун, не меняется при увеличении размеров регулярного участка заполнения. А размер сторон линейно зависит от сторон повторяющегося квадрата заполнения, в то время как число клеток этого квадрата растет квадратично :)
Поэтому для любого числа

, меньшего

, можно подобрать размер регулярного участка заполнения, при котором доля рыцарей на регулярном участке превысит

, а затем, увеличивая

и повторяя регулярный участок должное число раз, превысить

уже на всей площади.
ОбсуждениеНекоторые участники привели аккуратные выкладки, показывающие, что (недостижимая) верхняя грань доли рыцарей равна

.
Я не стал этого делать, посчитав приведенное выше рассуждения более прозрачными и, в то же время, достаточно строгими.
Приведу еще несколько конфигураций, с помощью которых можно сколь угодно подойти к доле рыцарей в

.
Заполнение "цепями" ("гармошками") было предложено Дмитрием Пашуткиным и Сергеем Половинкиным (названия их же):

Гармошки легко сужаются при приближении к краям площади.
Красиво смотрится "круговая" конфигурация, предложенная Николаем Дерюгиным:

Круговое заполнение можно сочетать с крестообразным:

Наконец, сразу несколько участников предложили ромбовидные конфигурации:

На последней картинке явственно просматриваются модные нынче мотивы самоподобия.
Сергей Половинкин попытался найти максимально возможное количество рыцарей для малых значений

. Мне довольно быстро удалось улучшить его результаты для большинства рассматриваемых

. Получилось так:

Очень может быть, что и эти значения не окончательны.
Участники, которые до подведения итогов тура успеют прислать улучшения, могут рассчитывать на дополнительные призовые баллы. (Улучшения для

и

оцениваются в 100 призовых баллов

)
НаградыЗа правильное, строго обоснованное решение задачи ММ140 Сергей Половинкин и Дмитрий Пашуткин получают по 12 призовых баллов.
Николай Дерюгин (он нашел необходимые конфигурации, но ошибся при оценивании доли рыцарей) получает 7 призовых баллов.
Анатолий Казмерчук и Алексей Волошин получают по 6 призовых баллов, А Евгений Гужавин - 5 баллов.
Эстетическая оценка задачи 4.6 баллаРазбор задачи ММ140 подготовил Владимир Лецко