Вопрос по статье о финслеровых углах

[Time]

В.О. в сообщении #437961 писал(а):

Хорошо, нулевое расстояние между точками это минимум.

Это не так. В $H_3$ нулевые расстояния не являются минимальными. Кроме нулевых тут возможны отрицательные, а при желании и гиперкомплексные. Я просто не хочу сейчас даже касаться этих моментов. Важно, что нулевые расстояния не минимальны..

В.О. в сообщении #437961 писал(а):

Максимум длинн кривых, соединяющих две точки (если расстояние действительно и неотрицательно) равен бесконечности. В евклидовом пространстве это очевидно. При движении от точки к точке можно бесконечно наматывать спираль ( почти одинаковые круги ) вокруг точки, так, чтобы длина кривой стала сколь угодно большой. В финслеровом пространстве практически то же самое, только немного аккуратней. Пусть между точками есть кривая ненулевой длины. Тогда чуть - чуть отступаем от концов и слегка варьируем кривую. Проходим расстояние туда и обратно. Получаем почти удвоенное раастояние. И так любое число раз. Максимум равен бесконечности.

Почему Вы упорно игнорируете возможность спокойно разобраться с аналогичными вопросами на псевдоевклидовой плоскости? Там не финслерова геометрия, а самая обычная квадратичная. Попробуйте описанную Вами процедуру проделать тут.

[В.О.]

Time в сообщении #438190 писал(а):

Это не так. В нулевые расстояния не являются минимальными. Кроме нулевых тут возможны отрицательные, а при желании и гиперкомплексные. Я просто не хочу сейчас даже касаться этих моментов.

И не надо касаться. В первом октанте, который подразумевался по умолчанию, все координаты положительны и норма положительна. Здесь минимум расстояния будет нулевым.

Time в сообщении #438190 писал(а):

Почему Вы упорно игнорируете возможность спокойно разобраться с аналогичными вопросами на псевдоевклидовой плоскости?

Я, как раз, очень спокойно и не торопясь разбираюсь. Мне еще никто ни на одну мою ошибку не указал. А вот Вы ошибаетесь на каждом шагу. Давайте не будем создавать нездоровую атмосферу.
Во-первых, псевдоевклидово пространство непосредственного отношения к данному вопросу не имеет. Но я готов для Вас разобраться и в нем, хотя это мне и не очень интересно.
Во-вторых, дайте , пожалуйста точную ссылку где решается уравнение Эйлера в псевдоевклидовом пространстве, о чем Вы говорили выше. По той ссылке , что Вы дали раньше решения уравнения Эйлера нет.

Тут возможен еще один вариант. Функционал длины кривой к нулю, в принципе, может подходить "остро", так, что производная не равна 0. Но и тогда должно существовать либо два (четное число) экстремумов, либо ни одного.

-- Вс апр 24, 2011 18:40:26 --

Решение уравнения Эйлера в статье имеет дефект, о котором я писал выше. Никто на это по существу не ответил. Вопрос остается открытым. Вполне может оказаться, что уравнение Эйлера решений не имеет.
Нужно аккуратное исследование решений уравнения Эйлера.

[Time]

В.О. в сообщении #438322 писал(а):

И не надо касаться. В первом октанте, который подразумевался по умолчанию, все координаты положительны и норма положительна. Здесь минимум расстояния будет нулевым.

В первом октанте положительны модули у векторов в нем лежащих, а Вы вроде бы как говорите о длинах кривых, которые вычисляются через дифференциалы компонент, которые в общем случае, даже лежа в нужном октанте, совсем не обязаны иметь направления внутри соответствующего изотропного конуса. Вы вон вообще хотели выше рассматривать изменение направления кривой, аж на противоположное.

В.О. в сообщении #438322 писал(а):

Во-первых, псевдоевклидово пространство непосредственного отношения к данному вопросу не имеет. Но я готов для Вас разобраться и в нем, хотя это мне и не очень интересно.

Вы мне ровно ничего не должны, как и я Вам. Не хотите, не разбирайтесь. Особенно, если не интересно.

В.О. в сообщении #438322 писал(а):

Во-вторых, дайте , пожалуйста точную ссылку где решается уравнение Эйлера в псевдоевклидовом пространстве, о чем Вы говорили выше. По той ссылке , что Вы дали раньше решения уравнения Эйлера нет.

Ту ссылку я давал предполагая, что хотите посмотреть, где описывается обратное неравенство треугольника. Про геодезические псевдоевклидовых пространств можно посмотреть в первом томе "Гравитации" Мизнера, Торна и Уилера парграф 13.4 и дополнение 13.3.
Там же можно найти и описание максимума длины времениподобных кривых, в случае совпадения их с аффинными прямыми.

В.О. в сообщении #438322 писал(а):

Решение уравнения Эйлера в статье имеет дефект, о котором я писал выше. Никто на это по существу не ответил. Вопрос остается открытым. Вполне может оказаться, что уравнение Эйлера решений не имеет.
Нужно аккуратное исследование решений уравнения Эйлера.

Ну, раз видите дефект, так попробуйте найти второй экстремум. Будет интересно посмотреть на соответствующий результат. В конце концов, второй вариант угла на индикатрисе $H_3$, на мой взгляд, давно напрашивается и выше мы об этом с Руст'ом говорили. Хотя я не думаю, что этот второй угол связан с индуцированной метрикой, ну да подождем аккуратного вывода..

[Time]

lavex в сообщении #437301 писал(а):

С самим пространством Минковского - да, никакой. Но я писал о квадрате интервала, т. е. геометрии с метрикой четвёртой степени. Чтобы получить "правильные знаки", нужно чтобы модуль определялся следующим выражением:
$|C_2|^4=[(-x^2+y^2)+(z^2+w^2)]^2=x^4+y^4+z^4+w^4-2x^2y^2-2x^2z^2-2x^2w^2+2y^2z^2+2y^2w^2+2z^2w^2$
Есть подозрение, что его можно добиться соответствующим выбором образующих из алгебры бикомплексных чисел. Правда, базис при этом останется ортогональным, а не изотропным, поэтому пока никаких выводов отсюда делать не стоит

Если б выбором базиса можно было добиться совпадения четвертой степени модуля пространства бикомплексных чисел с четвертой степенью интервала пространства Минковского, то это было бы одно и тоже пространство с одинаковыми группами симметрий, в том числе и изометрических. Но это, как известно, не так. Да и четырехкомпонентной алгебры с пространством Минковского никакой не связано, ни некоммутативной, ни неассоциативной, тем более нет связи с поличислами.

Цитата:

Теперь касательно изотропных векторов. Изложу процедуру поиска. Итак, для начала, по аналогии с двойными числами, берём биссектриссы положительных "октантов" (8 положительных и 8 отрицательных, в сумме - 16). Эти 8 биссектрисс оказываются "эллиптического" и "гиперболического" типа:
$k_1^e=1+i+I+iI, (k_1^e)^2=4i+4iI$; $k_1^h=1+i+I-iI, (k_1^h)^2=4I$;
$k_2^e=1-i+I-iI, (k_2^e)^2=-4i-4iI$; $k_2^h=1-i+I+iI, (k_1^h)^2=4I$;
$k_3^e=1+i-I-iI, (k_3^e)^2=4i-4iI$; $k_3^h=1+i-I+iI, (k_3^h)^2=-4I$;
$k_4^e=1-i-I+iI, (k_4^e)^2=-4i+4iI$; $k_4^h=1-i-I-iI, (k_4^h)^2=-4I$.
Далее всё просто, хотя пересчёт определённое время занял. Итак, изотропные вектора выражаются через биссектриссы следующим элементарным образом:
$e_1=\frac{k_1^e+k_2^e}{4}$; $e_2=\frac{k_3^e+k_4^e}{4}$;
$e_3=\frac{k_1^h+k_2^h}{4}$; $e_4=\frac{k_3^h+k_4^h}{4}$.
Легко убедиться, что так введённые изотропные векторы удовлетворяют основному свойству изотропии:
$e_je_le_me_n= \left\{\begin {array}{1} e_j, if [j=l=m=n],\\ 0, otherwise. \end {array}\right. $

Тут вроде бы все правильно.

Цитата:

Если я нигде выше не ошибся, что совершенно не исключено, выходит, что в изотропном базисе выражения, записанные в алгебре $C+C$ оказываются абсолютно аналогичными таковым в $H_4$, а всё различие, довольно значительное, кстати, проявляется в виде матрицы перехода и виде выражения в ортонормированном (трансверсальном) базисе. Ну и, понятно, что индикатрисса, будучи такой же 16-связной , имеет другой совершенно вид...

А вот этот вывод совершенно неверен.
Попробуйте получить в явном виде выражение для четвертой степени модуля бикомплексного числа в изотропном базисе и сравните его с аналогом четверных чисел. Особенно будет интересен разбор вопроса, как выглядят в пространстве бикомплексных чисел изотропные подпространства и сколько их, а также вопрос о том, сколько односвязных кусков у сферы этого пространства..

[Руст]

Цитата:

В конце концов, второй вариант угла на индикатрисе $H_3$, на мой взгляд, давно напрашивается и выше мы об этом с Руст'ом говорили. Хотя я не думаю, что этот второй угол связан с индуцированной метрикой, ну да подождем аккуратного вывода..

Я то как раз вводил метрику индуцированную (единственную индуцированную). Вдоль направления некоторого вектора а метрика финслерова пространства Минковского типа имеет вид:
$ds^2=dt^2-dl^2+o(dt^2+dl^2)$ (с точностью до членов третьего порядка), где $dt=0$ соответствует определению касательных векторов. Таким образом индуцируется метрика расстояний для одновременных событий для наблюдателя, соответствующего вектору а.
Суть манипуляций Кокорева заключается в том, что касательные векторы дополняются вектором а, чтобы не понизилось размерность пространства. Затем вводится структура исходного пространства гиперкомплексных чисел, который можно ввести в любом пространстве имеющей ту же размерность. Однако соглосования с исходной метрикой не может быть и речи. Когда исходное пространство есть пространство чисел, то на индикатрисе индуцируется структура группы Ли. Умножениям в группе будет соответствовать сложение (в касательном пространстве) логарифмов. А умножения для логарифмов нельзя определить естественным образом (функториально). Единственная естественная операция кроме сложения это структура алгебры Ли. Однако для коммутативных гиперкомплексных чисел это дает умножение с тождественным нулем.

[Time]

Руст в сообщении #439044 писал(а):

Суть манипуляций Кокорева заключается в том, что касательные векторы дополняются вектором а, чтобы не понизилось размерность пространства. Затем вводится структура исходного пространства гиперкомплексных чисел, который можно ввести в любом пространстве имеющей ту же размерность. Однако соглосования с исходной метрикой не может быть и речи.

Суть манипуляций Кокарева, в конце концов, приводит к совпадению им вводимых углов с аргументами экспоненциальной формы представления соответствующих рассматриваемому финслерову пространству поличисел. Уже одним этим все можно оправдать, даже если что-то не нравится. А вот у вас пока я не видел, ни конкретной формулы для вычислений для того же пространства $H_3$, ни связи так определяемого угла с какими то простыми алгебраическими параметрами. Проиллюстрируйте, пожалуйста, свои слова на конкретном примере поличисел $H_3$.

Руст в сообщении #439044 писал(а):

Когда исходное пространство есть пространство чисел, то на индикатрисе индуцируется структура группы Ли. Умножениям в группе будет соответствовать сложение (в касательном пространстве) логарифмов. А умножения для логарифмов нельзя определить естественным образом (функториально).

Можете сказанное проиллюстрировать на алгебре $H_2$? В крайнем случае на алгебре $H_3$. Я привык считать, что логарифмы как h-голоморфные функции достаточно естественно определяются в обоих случаях, в том числе и их умножение. Что именно по вашему мнению этому мешает?

Руст в сообщении #439044 писал(а):

Единственная естественная операция кроме сложения это структура алгебры Ли. Однако для коммутативных гиперкомплексных чисел это дает умножение с тождественным нулем.

Не понимаю. Беру два логарифма в алгебрах $H_2$ или $H_3$ и запросто перемножаю. Поясните, что вас в таком перемножении не устраивает?

[В.О.]

Time в сообщении #438928 писал(а):

Вы вон вообще хотели выше рассматривать изменение направления кривой, аж на противоположное.

Я надеюсь, что никто ничего против не имеет. А вот в формулах (22) в статье потерян знак модуля под интегралом. В третьем слева члене он есть, а в последнем нет. Это нехорошо. Собственно, это настолько плохо, что нет смысла проверять дальнейшие выкладки.

[Time]

В.О. в сообщении #439370 писал(а):

Я надеюсь, что никто ничего против не имеет.

Боюсь, что был бы против господин Эйнштейн, который, по сути, наложил запрет на превышение материальными телами скорости света, что геометрически отражается в запрете кривым мировым линиям иметь наклон больше, чем у образующих светового конуса, но Вам, похоже, это ни о чем не говорит, раз легко разворачиваете кривые в пространстве времени, аж, до обратного направления. Не мудрено, что после такой операции Ваша логика вступает в противоречие даже с тем, что давно устаканено в обычном пространстве-времени с квадратичным типом метрики.
На сколько я понимаю, работу по моей последней ссылке Вы даже не искали и не открывали?

В.О. в сообщении #439370 писал(а):

А вот в формулах (22) в статье потерян знак модуля под интегралом. В третьем слева члене он есть, а в последнем нет. Это нехорошо. Собственно, это настолько плохо, что нет смысла проверять дальнейшие выкладки.

Может, вместо констатации "плохости" сообщите, как именно такое опускание знака модуля повлияло на полученный результат?
К тому же, вместо качания головой и прочих ай-а-яй, гораздо лучше маленький, но конкретный результат. Нашли бы второе решение, или доказали, что найденное таковым не является.. А так, как говорится, одни междометия..

[В.О.]

Time в сообщении #439639 писал(а):

К тому же, вместо качания головой и прочих ай-а-яй, гораздо лучше маленький, но конкретный результат. Нашли бы второе решение, или доказали, что найденное таковым не является..

Time, Вы кажется, не поняли. У Вас в статье нашли ошибку. Грубую. Детскую. Все, что написано после этой ошибки можно забыть.
Правильный ответ я тоже Вам давно сказал. Минимальное расстояние по кривой между любыми двумя (в одном октанте) точками на индикатрисе равно нулю. Максимальное равно бесконечности. Это как раз, тот самый маленький, но конкретный результат. Вы это не считаете результатом? Да считайте чем угодно. Мне без разницы.
И Эйнштейн здесь совершенно не при чем. Мы находимся даже не псевдоевклидовом, а в абстрактном финслеровом пространстве, с какой-то придуманной Вами "метрической" функцией. К реальности эта метрика никакого отношения не имеет.

[Time]

В.О. в сообщении #439881 писал(а):

Вы кажется, не поняли. У Вас в статье нашли ошибку. Грубую. Детскую. Все, что написано после этой ошибки можно забыть.

В.O., Вы не знаете и знать не хотите геометрии псевдоевклидовой плоскости. Пытаетесь в пространствах аналогичных этой плоскости мыслить римановыми представлениями. И после этого утверждаете о каких-то детских ошибках в ситуациях, о которых не имеете даже начального представления. Ну, что ж, видать Вам не судьба хоть в чем ни будь разобраться. Идите себе с мирром.. Со школой Вы были правы, записываться Вам точно туда не стОит.

В.О. в сообщении #439881 писал(а):

Правильный ответ я тоже Вам давно сказал. Минимальное расстояние по кривой между любыми двумя (в одном октанте) точками на индикатрисе равно нулю. Максимальное равно бесконечности. Это как раз, тот самый маленький, но конкретный результат. Вы это не считаете результатом?

Если не рассматривать отрицательных расстояний (хотя в пространствах типа $H_3$ такие вполне возможны), то с первой половиной Вашего утверждения еще можно согласиться. А вот что касается бесконечно больших расстояний, то это идет вразрез с принятой сегодня логикой на той же псевдоевклидовой плоскости. Я Вам давал ряд ссылок, с которыми Вы не ознакомились, хотя формально сами же их и просили. Вот уж где детское упрямство, так это тут. Я не собираюсь его ломать, оставайтесь при своих убеждениях.

В.О. в сообщении #439881 писал(а):

И Эйнштейн здесь совершенно не при чем. Мы находимся даже не псевдоевклидовом, а в абстрактном финслеровом пространстве, с какой-то придуманной Вами "метрической" функцией. К реальности эта метрика никакого отношения не имеет.

На последок осмелюсь вопреки Вашему упрямству, все же дать совет пересилить себя и разобрать полностью аналогичную ситуацию с максимальными и минимальными расстояниями на псевдоевклидовой плоскости. Без этого разбираться Вам с геометрией финслеровых пространств совершенно бессмысленно.

[В.О.]

Time в сообщении #439900 писал(а):

Со школой Вы были правы

Ну вот видите, в чем то я могу быть правым. Может я прав и еще в чем-то?
Time, Вы зря ругаться изволите. Вы еще не поняли, чем нулевые расстояния грозят Вашим физическим теориям. Вам бы не ругаться, а крепко подумать.
И школа эта...Вы там как-то сам с собой ... сначала поманили пряником... потом отлучили от пряника...а я как жил так и живу, вполне себе доволен.
Давайте - ка я, чтобы разрядить обстановку, расскажу анекдот в тему.

Два ковбоя ехали по прерии и увидели на дороге груду бизоньего навоза. Остановились и стали разглядывать ее.
- Билл, cъешь эту кучу за тысячу долларов?
Билл подумался и согласился. Не торопясь все съел. Джон отсчитал тысячу и поехали дальше.
Через пару часов они увидели еще одну груду бизоньего навоза.
- Джон, а ты за тысячу долларов это съел бы?
Джон съел и получил тысячу. Поехали дальше.
Через пару часов Джон остановил лошадь и повернулся к Биллу:
- Послушай, а тебе не кажется, что мы оба наелись дерьма бесплатно?

[Time]

В.О. в сообщении #439942 писал(а):

Time, Вы зря ругаться изволите.

Я не ругаюсь. Просто констатирую имеющийся уровень и отсутствие перспектив.

В.О. в сообщении #439942 писал(а):

Вы еще не поняли, чем нулевые расстояния грозят Вашим физическим теориям.

Примерно тем же, чем нулевые расстояния (интервалы) грозили СТО и ОТО.
Беда не в том, что Вы не знакомы с псевдоевклидовой плоскостью и ее геометрическими особенностями, настоящая проблема в упрямом нежелании даже знакомиться.

В.О. в сообщении #439942 писал(а):

И школа эта...Вы там как-то сам с собой ... сначала поманили пряником... потом отлучили от пряника...а я как жил так и живу, вполне себе доволен.

Вот именно, как жили, так и будете жить, даже не подозревая, что можно жить иначе..

[Руст]

Цитата:

Суть манипуляций Кокарева, в конце концов, приводит к совпадению им вводимых углов с аргументами экспоненциальной формы представления соответствующих рассматриваемому финслерову пространству поличисел. Уже одним этим все можно оправдать, даже если что-то не нравится.

Для этого не требуется определение умножений для логарифмов. Касательные веекторы и так будут представлять логарифмы даже если числа не коммутативные.

Цитата:

А вот у вас пока я не видел, ни конкретной формулы для вычислений для того же пространства $H_3$, ни связи так определяемого угла с какими то простыми алгебраическими параметрами. Проиллюстрируйте, пожалуйста, свои слова на конкретном примере поличисел $H_3$.

Касательное пространство около вектора a на индикатрисе представляется векторами $ab$ для $H_n$, где $tr(b)=0$. Ортонормированный базис состоит из $ab_i$, где $b_i$ вектора у которых в матричном представлении все нули за исключением двух соседних элементов на диагонали (след равен нулю).

Цитата:

Можете сказанное проиллюстрировать на алгебре $H_2$? В крайнем случае на алгебре $H_3$. Я привык считать, что логарифмы как h-голоморфные функции достаточно естественно определяются в обоих случаях, в том числе и их умножение. Что именно по вашему мнению этому мешает?

Ничего не мешает. В случае $H_4$ с таким же успехом лучше определить кватернионное умножение. Хотя такое умножение так же не естественно, однако он согласуется с ним хотя бы топологический (метрического согласования по видимому все равно не получится).

Цитата:

Не понимаю. Беру два логарифма в алгебрах $H_2$ или $H_3$ и запросто перемножаю. Поясните, что вас в таком перемножении не устраивает?

Уже много раз подчеркивал не естественность, математическим языком не функториальность. Индикатриса для числового пространства является однородным пространством. Соответственно умножение на элементы группы Ли (числа с единичной нормой) задают естественные изоморфизмы между касательными пространствами индикатрисы в разных точках. Однако, они являются только изоморфизмами только для структуры векторного пространства, максимум можно сделать изоморфизмами алгебры Ли, но не как поличисел (для коммутативных алгебр чисел, это нулевое умножение). Об этой не естественности и идет речь.

Что касается спора между вами и В.О., то он больше прав. Кстати определяя на касательном пространстве с расширением структуру $H_n$ по Кокореву как раз получим метрику на индикатрисе, что минимум равен 0, максимум бесконечность. У меня вся метрика локально сводится к отрицательно определенной Римановой метрике. Точное индуцирование не получается. Меняя знаки получаем не $ds^2$, а метрику $dl^2$ связанный с первым соотношением $ds^2=dt^2-dl^2$.

[Kallikanzarid]

Руст в сообщении #440202 писал(а):

Для этого не требуется определение умножений для логарифмов. Касательные веекторы и так будут представлять логарифмы даже если числа не коммутативные.

Руст в сообщении #440202 писал(а):

Уже много раз подчеркивал не естественность, математическим языком не функториальность.

Time не поймет, о чем вы, он не знает ни дифференциальную геометрию, ни теорию категорий.

[Time]

Руст в сообщении #440202 писал(а):

Для этого не требуется определение умножений для логарифмов. Касательные веекторы и так будут представлять логарифмы даже если числа не коммутативные.

Давайте рассмотрим некоммутативную алгебру обычных вещественных кватернионов. Им соответствует четырехмерное евклидово пространство. Покажите как касательные вектора этого пространства собой "представляют логарифмы"? Я так понимаю, что Вы, по сути, говорите о возможности введения для кватернионов экспоненциальной формы представления, на подобии экспоненциальной формы представления комплексных чисел, как и у тех с одним модулем, но с несколькими аргументами? Не покажите в формулах, как выглядит такая экспоненуиальная форма представления для кватернионов? Если покажите, то с логарифмом станет ясно на автомате, на основании того, что та является обратной функцией к экспоненциальной.. Боюсь только, что конкретных примеров я так и не увижу..

Цитата:

Касательное пространство около вектора a на индикатрисе представляется векторами $ab$ для $H_n$, где $tr(b)=0$. Ортонормированный базис состоит из $ab_i$, где $b_i$ вектора у которых в матричном представлении все нули за исключением двух соседних элементов на диагонали (след равен нулю).

Я просил дать определение не ОРТОГОНАЛЬНОСТИ или прямого угла, а ПРОИЗВОЛЬНОГО угла, причем доведенное до КОНКРЕТНОЙ формулы. У Кокарева это есть, у Вас я не видел. Пока только намеки вокруг да около.

Цитата:

Уже много раз подчеркивал не естественность, математическим языком не функториальность. Индикатриса для числового пространства является однородным пространством. Соответственно умножение на элементы группы Ли (числа с единичной нормой) задают естественные изоморфизмы между касательными пространствами индикатрисы в разных точках. Однако, они являются только изоморфизмами только для структуры векторного пространства, максимум можно сделать изоморфизмами алгебры Ли, но не как поличисел (для коммутативных алгебр чисел, это нулевое умножение). Об этой не естественности и идет речь.

То, что язык классической дифференциальной финслеровой геометрии не годится для описания линейных финслеровых пространств связанных с поличислами я говорю давно и постоянно. Для меня совсем не удивительно, что пытаясь использовать конструкции первой для описания пространства вторых ни у вас, ни у кого то другого ничего конструктивного и естественного не получается. До тех пор, пока вы не перейдете на описание соответствующих пространств при помощи аппарата скалярного полипроизведения, у вас только и будут что появляться всякие "неестественности". 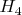Однако вы легко можете меня убедить в обратном: приведите конкретный результат применительно хотя бы к одному из пространств связанных с алгеброй $H_3$ или $H_4$ полученный на основе классического аппарата финслеровой геометрии и покажите как он реализуется в самой алгебре. Пока же я вижу одни только обещания.

Цитата:

Что касается спора между вами и В.О., то он больше прав. Кстати определяя на касательном пространстве с расширением структуру $H_n$ по Кокореву как раз получим метрику на индикатрисе, что минимум равен 0, максимум бесконечность. У меня вся метрика локально сводится к отрицательно определенной Римановой метрике. Точное индуцирование не получается. Меняя знаки получаем не $ds^2$, а метрику $dl^2$ связанный с первым соотношением $ds^2=dt^2-dl^2$.

У вас, что, как и у B.O. есть сомнения в правильности получения конкретного решения уравнения Лагранжа-Эйлера для экстремалей на единичной сфере пространства $H_3$ в первом октанте? Можно подробнее об этих сомнениях? Что именно не устраивает? Решение принципиально неверно найдено? Или видите еще и другие решения? Что то иное? В любом случае, просьба обосновать свое утверждение..
По поводу максимума связанного с бесконечностью длины кривой.. У вас он также связан с многократным обходом по кривой и обратно, как это предлагает B.O., или с другими соображениями? Если так же, может от вас я услышу как такое утверждение соотносится с общепринятыми аналогичными свойствами длин экстремальных кривых на псевдоевклидовой плоскости, где, как известно, максимальные времениподобные расстояния между парамети точек не бесконечные, а конечные и когда кривые совпадают с аффинными прямыми. Или на псевдоевклидовой плоскости ваше с B.O. утверждение также "более верно", чем общепринятое понимание соответствующего вопроса?