То есть отвечать на вопросы вы отказываетесь, предлагая мне вместо этого продираться через ваш сайт? Хоть ссылку на конкретное видео дайте :\
Предыдущий мой пост был ответом на реплику
Someone, просто ваши вопросы появились чуть раньше, чем я успел нажать "отправить". Ответы на ваши вопросы - ниже. Ссылку на видео я давал, неужели так трудно сориентироваться на относительно небольшой странице? Хорошо, даю прямую ссылку:
http://hypercomplex.xpsweb.com/video/20 ... okarev.mkvTime, давайте еще раз:
Можно было бы и повежливей, тем более, что ответы уже давались, ну да ладно, пройдемся еще раз, но с некоторыми добавлениями..
1) Определение конформности в финслеровой геометрии.
В финслеровой геометрии связанной с коммутативно-ассоциативными гиперкомплексными числами (точно так же как и в евклидовой или псевдоевклидовой геометрии) определение конформности можно ввести тремя почти равноценными способами (через метрику, через сохранение углов, и через преобразования бесконечномалых сфер в бесконечно малые сферы). Надеюсь, пока будет достаточно одного. Конформными будем называть преобразования, сохраняющие финслеровы углы. Под углом же в этом случае понимается финслерово расстояние вдоль экстремали лежащей на единичной сфере (индикатрисе) между концами пары единичных векторов, выходящих из ее центра. Подробнее о введении в соответствующих пространствах понятия угла можно посмотреть в:
http://hypercomplex.xpsweb.com/articles ... /11-04.pdfна примере трехмерного пространства, связанного с алгеброй тройных чисел (трехмерного обобщения двойных чисел). Что бы не тратить время на не относящиеся к углу моменты можно ограничиться введением и разделом 4. В разделах 5 и 6 показано, как от определения угла перейти к конкретным формулам.
2) Определение основных дифферециальных операторов и связь конформности с аналитичностью.
Определение аналитической функции можно найти в книге Гарасько на стр. 65
http://hypercomplex.xpsweb.com/articles ... -gbook.pdfОпределение основных дифференциальных операторов - на стр. 149-152 этой же ссылки.
Связь конформности и аналитичности показана на стр. 153.
3) Чем хороша богатая группа конформных преобразований на примере, чтобы мне было понятнее.
Выше я уже давал ссылку на доклад Кокарева (похоже как и
Someone вы его так и не скачали). Надеюсь, у вас меньше причин упорствовать и не смотреть, раз уж хотите познакомиться с конкретным примером полезности богатых групп конформных преобразований. После того как познакомитесь с докладом, можно вернуться к книге Гарасько:
http://hypercomplex.xpsweb.com/articles ... -gbook.pdfСо стр. 235 идет описание гиперкомплексного аналога теории комплексного потенциала, на случаи финслеровых пространств с одной из коммутативно-ассоциативных алгебр.
Если два этих конкретных примера не убедят вас в полезности бесконечных групп конформных преобразований и связанных с ними аналитических функций (но только в случае ознакомления, а не заочно как это было у
Someone ), готов извиниться за напрасно отнятое ваше время.
4) Можно таблицу умножения ваших алгебр и, заодно, норму на них или что там у вас вместо нее.
В частности мы часто рассматриваем ассоциативно-коммутативную трехкомпонентную алгебру, обозначаемую

, которой соответствует простейшее трехмерное финслерово пространство с кубической метрической функцией и являющуюся трехмерным обобщением более известной алгебры двойных чисел

, которой соответствует геометрия двумерного псевдоевклидова пространства-времени.
И таблица умножения, и вид модуля числа, и метрическая функция соответствующего пространства, и много что еще по этой алгебре выложено на стр. 66-72 книги Гарасько.
Другой наиболее часто рассматриваемой нами коммутативно-ассоциативной алгеброй является алгебра, четырехкомпонентного расширения алгебры двойных чисел, обозначаемая
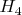
. Ее таблицы умножения и др. свойства в разных базисах представлены на стр. 154-163 той же книги Гарасько. Именно эта алгебра, вернее соответствующее ей четырехмерное финслерово пространство, нами рассматривается как максимально близкое к пространству-времени Минковского, с тем отличием, что конформные преобразования в нем образуют не 15-параметрическую, а бесконечную группу, а интервал связан не с квадратичной формой, а четвертого порядка. Если посмотрите, то увидите, что с кватернионами и с бикватернионами данная алгебра не имеет ничего даже отдаленно общего.
5) Вы утверждаете, что аналитические функции на ваших алгебрах будут вести себя так же хорошо, как и обычные голоморфные. Я сомневаюсь, что это так. Убедите меня. На худой конец дайте ссылку на статью в рецензируемом журнале, где это объясняется (на ваш сайт не надо, спасибо).
Вам знакомы не обычные голоморфные функции комплексной переменной, а ее гиперболические аналоги, называемые иногда h-голоморфными функциями двойной переменной? Думаю что нет, поэтому перед тем как убеждать вас в аналогичных свойствах h-голоморфных функций "наших" многокомпонентных коммутативно-ассоциативных алгебр, предлагаю прочитать пару статей именно о первых по ссылке:
http://hypercomplex.xpsweb.com/articles ... ngp_13.pdf 1) h-голоморфные функции двойной переменной стр. 44-77;
2) Гиперболическая теория поля на плоскости двойной переменной стр. 78-127.
Среди примеров h-голоморфных функций двойной переменной разобраны аналоги, и логарифмической функции, и обратной, и степенной, и функции Жуковского. Причем с графическими иллюстрациями особенностей векторных полей, им соответствующих.
Что касается шпильки про наш сайт и готовности изучать статьи лишь в рецензируемых журналах - пока пропущу ее мимо ушей.



