maxal, спасибо, что не поленились и написали. Правда, Вы где-то умудрились потерять серию решений

, где

--- натуральное

. Я приведу ещё один способ решения, тоже в каком-то смысле естественный.
При

подходит любое

. Далее считаем

. Пусть

т.е.

. Дискриминант

этого уравнения, рассматриваемого как квадратное относительно

, должен быть точным квадратом. Докажем, что если

, то

и, как следствие,

. Действительно, если

, то, как нетрудно проверить,

Если же

, то справедливы неравенства

Таким образом, в каждом из этих случаях

заключен между квадратами двух последовательных натуральных чисел и потому не может быть точным квадратом. Осталось рассмотреть случаи

и

. В первом из них имеем

для любого

, а из оставшихся значений

подходит только
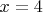
(и тогда

или

). Во втором случае

при любом

, так что новых решений не будет.