Выходит, что суммирование идёт по n, которое колеблется в интервале, длиной

, а

, в свою очередь, стремится к бесконечности. Меня это настораживает.
Кроме того, чтобы в дальнейших рассуждениях всё пошло гладко,

должна стремиться к нулю, но тогда в дроби

возникает неопределённость, так как

.
Я с радостью согласился бы с
_hum_. Мне сложно сформулировать, что именно меня смущает, но, боюсь, у преподавателя это получится лучше...
Все потому, что вы слишком формально подходите к доказательству, а полезнее иногда подумать, в чем суть манипуляций. Что нужно? Правильно - убедиться, что при любом фиксированном

величину

за счет выбора больших

можно сделать сколь угодно мало отличной от нуля, или, если более формально, что для всякого

существует такое

, что при всех

данная величина по модулю не будет превосходить

. Что может способствовать тому, что с ростом

наша величина (сумма) будет становиться меньше? Ну, в первую очередь напрашивается ЦПТ, которая в случае, если удастся в

"лямбду"{} заменить на

, гарантирует при достаточно больших

равномерную малость

. Однако, этого недостаточно, так как ЦПТ срабатывает при больших

, а у нас в сумме участвуют и малые. Таким образом, надо как-то увидеть, за счет чего при малых

слагаемые могут быть малыми. Ответ подсказывает тот факт, что

является одновременно и матожиданием, вокруг которого, как известно из того же правила "трех сигма", сосредоточена большая часть распределения, а это значит, что с его ростом коэффициенты
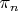
с малыми номерами

должны уменьшаться. Это нам и нужно. Остается теперь только все это записать. В первую очередь, выразим

через

. Вводя обозначение

и замечая, что

, получаем
![\begin{align*}
\Delta_\lambda^n(u) = \Delta_n^n\Big( r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) + \bigg [\Phi\Big( r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) - \Phi(u)\bigg]
\end{align*} \begin{align*}
\Delta_\lambda^n(u) = \Delta_n^n\Big( r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) + \bigg [\Phi\Big( r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) - \Phi(u)\bigg]
\end{align*}](https://dxdy-03.korotkov.co.uk/f/6/f/d/6fd34f2a8dc6e5d32a51ecec926a84ce82.png)
Отсюда видно, что для малости

дополнительно требуется еще и чтобы

не слишком сильно отличалось от единицы (разность значений

была малой). Этого мы можем попытаться добиться за счет рассмотрения только слагаемых с подходящими значениями номеров

, надеясь, что все остальные не дают существенного вклада в общую сумму. В противном случае идея доказательства не пройдет. К счастью, все получается: если для
всякого

ввести множество подходящих номеров

то, как следует из неравенства Чебышева,

а значит, действительно, при достаточно больших

слагаемыми с номерами

, не попадающими в

, можно будет пренебрегать. Ну и все.
Теперь, имеем, при любых

:
![\begin{multline*}
\sum_{n = 0}^\infty \pi_n
\Delta_\lambda^n(u) = \sum_{D_{\lambda}^{\varepsilon}}^\infty
\pi_n \Delta_\lambda^n(u) + \sum_{\mathbb{N}\setminus
D_{\lambda}^{\varepsilon}}^\infty \pi_n \Delta_\lambda^n(u) = \\
\sum_{D_{\lambda}^{\varepsilon}}^\infty \pi_n \Delta_n^n\Big(
r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) +
\sum_{D_{\lambda}^{\varepsilon}}^\infty \pi_n \bigg [\Phi\Big(
r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) - \Phi(u)\bigg]
+ \sum_{\mathbb{N}\setminus
D_{\lambda}^{\varepsilon}}^\infty \pi_n \Delta_\lambda^n(u).
\end{multline*} \begin{multline*}
\sum_{n = 0}^\infty \pi_n
\Delta_\lambda^n(u) = \sum_{D_{\lambda}^{\varepsilon}}^\infty
\pi_n \Delta_\lambda^n(u) + \sum_{\mathbb{N}\setminus
D_{\lambda}^{\varepsilon}}^\infty \pi_n \Delta_\lambda^n(u) = \\
\sum_{D_{\lambda}^{\varepsilon}}^\infty \pi_n \Delta_n^n\Big(
r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) +
\sum_{D_{\lambda}^{\varepsilon}}^\infty \pi_n \bigg [\Phi\Big(
r_{\lambda,n}^{-\frac{1}{2}}\,\, u\Big) - \Phi(u)\bigg]
+ \sum_{\mathbb{N}\setminus
D_{\lambda}^{\varepsilon}}^\infty \pi_n \Delta_\lambda^n(u).
\end{multline*}](https://dxdy-03.korotkov.co.uk/f/a/9/b/a9bdcc9d4c2fdd05f6468503a6c8c13682.png)
Для всякого

за счет непрерывности

можем выбрать такое

, чтобы для всякой точки

выполнялось

. Тем самым сделаем разность во второй сумме не превосходящей по абс. величине значение

. После этого выберем такое большое

, чтобы первая сумма по ЦПТ, а третья по неравенству Чебышева были по абс. значению меньше

. Тем самым получим, что и вся сумма не будет по абс. значению превосходить

. Ч.т.д.
P.S. И да, не отказывайтесь от доказательства
Хорхе - оно проще и красивее, единственно, надо только его сознать, чтобы потом Вас подобно замечаниям
yt,sdfksq не сбивали с толку.



