Здравствуйте!
Начал решать задачи по системе уравнений и вот задача, которую я решить не смог:
Два пешехода отправились одновременно навстречу друг другу из пунктов

и

, расстояние между которыми

км. Через

часа расстояние между ними сократилось до

км, а ещё через

часа первому пешеходу осталось пройти до пункта N на

км меньше, чем второму до M. Найдите скорости пешеходов.
Моё решение:
Как обычно я пытался составить уравнение, но ничего не получалось. Т.к. до этого я решал только задачи, где за определённый промежуток времени что-либо двигалось в одном направлении. А тут получается оба пешехода сначала двигались друг к другу, а затем в разные стороны.
Значит сперва я разбил составление уравнения на две части. Тот промежуток, в на котором они шли друг к другу, и тот, на котором они шли в разные стороны.
1. Вот какое уравнение я составил:
![$\left\{\begin{array}{l}
{x+y=38}
\\[5pt]{x-y=2}
\end{array}\right$ $\left\{\begin{array}{l}
{x+y=38}
\\[5pt]{x-y=2}
\end{array}\right$](https://dxdy-03.korotkov.co.uk/f/e/b/1/eb18e46d89731d06ff1fe42a72c6c97182.png)
Получилось

;

Значит первый прошёл за

часа

км, второй прошёл

км.
2. Теперь найдём скорости на пройденном пути:

километров в час

километров в час
3. В задаче ведь не сказано, что на протяжении пути их скорости менялись. Поэтому, я решил проверить - полученные мною скорости пешеходов не является ли ответом на задачи.
Поэтому задал вопрос - сколько пройдут пешеходы за следующие

часа.
Первый пешеход пройдёт

км; Второй пешеход

км.
А поскольку первый пешеход уже прошёл за

часа

км, то за

часов он должен пройти при данной своей скорости

км.
Второй должен пройти

км.
По условию задачи первому осталось после

часов пути пройти до пункта на

км меньше, чем второму. А по моему решению он уже прошёл
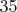
км. И ему осталось пройти до пункта всего

километра, что не соответствует условию задачи. К тому же второй прошёл меньше него всего лишь на

км.
4. Делаю вывод, что это решение задачи неправильно.
Пробовал я решить и другими способами, но пока что у меня решение не получается.



