Решение школьных задач и примеров

[maxmatem]

Цитата:

1. Составляю первое уравнение и второе, получается система уравнений:
$\left\{\begin{array}{l} {\frac{10}{3}x+\frac{10}{3}y=30} \\[5pt]{4.5x+2.5y=30} \end{array}\right$

Можно решать и в лоб, но лучше немного упростить эту систему.Первое уравнение умножите на $3$. А второй на $4$и получите такую систему равносильную исходной.
$\[ \left\{ \begin{gathered} 10x + 10y = 90 \hfill \\ 18x + 10y = 120 \hfill \\ \end{gathered} \right. \] $

Ну а затем вычтите из второго первое уравнение и сразу найдёте переменную $x$.

[AKM]

ximikat в сообщении #416041 писал(а):

Но с ответом моё решение не совпадает.
Значит я где-то допустил ошибку в вычислениях. А где, не пойму?

Раз Вам известен ответ, Вы можете его подставить в саму исходную систему, и проверить, правильно ли она составлена. Если окажется, что правильно, то те же подстановки в дальнейшие Ваши действия помогут определить, где именно Вы ошиблись.

Так же можно поступить и с найденным Вами решением. Подставить в первое уравнение. Потом в следующее. Потом в следующее. Потом в следующее. Потом в следующее.

-- 23 фев 2011, 13:53 --

ИСН в сообщении #415406 писал(а):

...Так запишите это что-то жирным шрифтом вверху листа, и ему следуйте. Типа "я ввёл переменную $x$, она значит..."

Вам уже указали --- объясняйте людям, кто такой у Вас икс, кто такой игрек. А Вы упрямствуете. А мы не телепаты.

[spaits]

ximikat в сообщении #416041 писал(а):

Здравствуйте, ребята!
MrDindows, spaits спасибо, что помогли мне по прошлой задаче. Я к сожалению ответить не смог в тот день, т.к. неожиданно у меня подскочила температура и сейчас я болею гриппом.

Сегодня ещё одна задача. Самое интересно в том, что у меня уже получилось составить систему уравнений, а решить её не получается.
Вот задача:

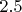
Из пунктов $A$ и $B$, расстояние между которыми $30$ километров, навстречу друг другу вышли два пешехода и встретились через $3$ часа $20$ минут. Если бы первый вышел на $2$ часа раньше второго, то встреча произошла бы через $2.5$ часа после выхода второго. Найдите скорость пешеходов.

Моё решение
1. Составляю первое уравнение и второе, получается система уравнений:
$\left\{\begin{array}{l} {\frac{10}{3}x+\frac{10}{3}y=30} \\[5pt]{4.5x+2.5y=30} \end{array}\right$
2. Теперь пытаюсь вычислить это уравнение при помощи метода подстановки.
В первом уравнении выражаю $x$ через $y$:
$\frac{10}{3}x+\frac{10}{3}x=30$
$\frac{10}{3}x=30-\frac{10}{3}y$
$x=30*\frac{3}{10}-\frac{10}{3}y*\frac{3}{10}$
$x=9-y$

Подставляю $x$ во второе уравнение:
$4.5(9-y)+2.5y=30$
$40.5-4.5y+2.5y=30$
$-2.5y=-10.5$ $y=4.2$
Тогда $x$:
$x=9-4.2=4.8$
Но с ответом моё решение не совпадает.
Значит я где-то допустил ошибку в вычислениях. А где, не пойму?

Надо же, Химикат, напутали в самом конце!
Всё верно до места: 40,5-4,5у+2,5у=30.
Дальше будет: 10,5=2у; у=5,25; х=3,75.
Конечно, скорости выражены в километрах в час.

За такую невнимательность вот Вам детская задача с конфетками.
Задача.
На столе n конфет, n - натуральное число (чтобы Вы не подумали, что я Вам даю огрызки конфет). Двое играют в такую игру: каждый по очереди съедает столько конфет, чтобы их число равнялось квадрату натурального числа. Проигрывает тот, кому не остаётся конфет.
Доказать, что существует бесконечно много таких n, при которых второй игрок при правильной стратегии обязательно выигрывает. Примечание: здоровье у обеих отменное.

[Toucan]

spaits,
замечание за искажение ника, избыточное цитирование и неиспользование $\TeX$ при наборе формул.

[Someone]

ximikat в сообщении #416041 писал(а):

$40.5-4.5y+2.5y=30$
$-2.5y=-10.5$

Интересно, а $4{,}5-2{,}5$ - это сколько?

(Оффтоп)

У меня такое впечатление (не только по этой задаче), что ximikat - это тролль, успешно прикидывающийся придурком.
Прошу прощения, если не прав.

[gris]

Опять бесовские системы. Скорость сближения составляет 30/3.20=9 км/ч. За два с половиной часа совместной прогулки они прошли 22,5 км. Значит первый за два часа прошёл 7,5 км. То есть его скорость 3,75 км/ч, а второго 5,25 км/ч.

[ximikat]

Уважаемый AKM
я так и делаю, всё время проверяю ответ в уравнениях.

(Оффтоп)

АКМ я так понимаю Авангард Красной Молодёжи? Просто интересно?

Уважаемый spaits!
Спасибо Вам большое за подсказку. Да уж перестарался я над этой задачей. Поэтому и не углядел в конце ошибке.
А начальное условие Вашей задачки я не совсем понял. Очень похожа, видимо, на задачку про зёрна на шахматной доске". Значит первый съедает $1$ конфету, а второй $1^2=1$. Оба съели две конфеты. На второй раз первый ест $2$, а второй я так понимаю $2^2=4$. На третий раз первый ест $4$, а второй $4^2=16$ конфет. Такое я понимаю условие в задаче, или я что-то неправильно понял?

-- Ср фев 23, 2011 13:59:01 --

Здравствуйте, уважаемый gris!
У меня так как у Вас не получается - сколько ни пробовал. А если бы получалось, я бы только и решал все задачи методом рассуждения.
Даже в этом вашем решении - как Вы получили эти 22.5?
Значит мне надо тренировать этод метод на более простых задачах. Пока Вы тут - может быть найдёте для меня такую задачу, которую я бы мог решить методом рассуждения?

[spaits]

А начальное условие Вашей задачки я не совсем понял. Очень похожа, видимо, на задачку про зёрна на шахматной доске". Значит первый съедает $1$ конфету, а второй $1^2=1$. Оба съели две конфеты. На второй раз первый ест $2$, а второй я так понимаю $2^2=4$. На третий раз первый ест $4$, а второй $4^2=16$ конфет. Такое я понимаю условие в задаче, или я что-то неправильно понял?

Уважаемый Ximikat! Опять Вы неправильно поняли, не может никто из них съесть 2 конфеты - число конфет должно равняться квадрату натурального числа!
И почему Вы считаете, что вначале первый берёт 1 конфету? Не обязательно. Правда, если на столе осталось, например, 3 конфеты, он берёт одну, так как 4 взять не может (их нет).

-- Ср фев 23, 2011 13:17:58 --

$9*2,5=22,5$

[ximikat]

Ну предположим, что
на столе $3$ конфеты. Первый съедает $1^2$, второй съедает $1^2$, первый съедает $1^2$. Проигрывает второй (и стратегии тут другой быть не может).
на столе $5$ конфет. Тогда первый съедает $2^2$ второй съедает $1^2$. Проигрывает первый.
На столе $6$ конфет. Первый съедает $2^2$ второй съедает $1^2$. И первый $1^2$. На столе конфет не остаётся. Проигрывает второй (тоже нет другой стратегии).
На столе $7$ конфет. То же самое, только $7$ конфету съедает второй. Проигрывает первый.
На столе $8$ конфет. Оба съедают по $2^2$. Проигрывает первый.
Значит отсюда вывод - не всегда срабатывает стратегия, чтобы второй съел последнюю конфету.

[gris]

Опять Вы скатываетесь на цифры.
Это уж задача на чисто рассуждения. А предположим, что существует только конечное число таких количеств конфет, при которых выигрывает второй игрок. А при остальных выигрывает первый. А кто первый, а кто второй? Вот в этой сермяжной правде и скрыт ответ: Сегодня ты первый, а завтра тебя убили совковой лопатой и зарыли на помойке.

[spaits]

ximikat в сообщении #416113 писал(а):

Ну предположим, что
на столе $3$ конфеты. Первый съедает $1^2$, второй съедает $1^2$, первый съедает $1^2$. Проигрывает второй (и стратегии тут другой быть не может).
на столе $5$ конфет. Тогда первый съедает $2^2$ второй съедает $1^2$. Проигрывает первый.
На столе $6$ конфет. Первый съедает $2^2$ второй съедает $1^2$. И первый $1^2$. На столе конфет не остаётся. Проигрывает второй (тоже нет другой стратегии).
На столе $7$ конфет. То же самое, только $7$ конфету съедает второй. Проигрывает первый.
На столе $8$ конфет. Оба съедают по $2^2$. Проигрывает первый.
Значит отсюда вывод - не всегда срабатывает стратегия, чтобы второй съел последнюю конфету.

А этого и не требовалось, чтобы всегда выигрывал второй. Требуется доказать, что при правильной стратегии число выигрышей второго будет бесконечным, какой бы первый ход ни сделал первый.
Это же можно сказать другими словами: при правильной стратегии обеих число проигрышей первого игрока бесконечно.
Вы сами привели несколько примеров, когда проигрыш первого предопределён.
Но докажите, что число таких примеров бесконечно.

-- Ср фев 23, 2011 13:58:54 --

gris в сообщении #416122 писал(а):

Опять Вы скатываетесь на цифры.
Это уж задача на чисто рассуждения. А предположим, что существует только конечное число таких количеств конфет, при которых выигрывает второй игрок. А при остальных выигрывает первый. А кто первый, а кто второй? Вот в этой сермяжной правде и скрыт ответ: Сегодня ты первый, а завтра тебя убили совковой лопатой и зарыли на помойке.

Первый - это тот, который делает первый ход.
Встанут они, убитые за колючей проволокой, когда мы очистим землю. Вы и я.

[gris]

Я ничего чистить не собираюсь.
А вот после того, как первый сделал ход, кто будет первым?

[spaits]

gris в сообщении #416130 писал(а):

Я ничего чистить не собираюсь.
А вот после того, как первый сделал ход, кто будет первым?

Пожалуйста, Ваш выбор, никто не заставляет.
Но Ваше замечание о первом и втором справедливо. Условно тот, кто сделал второй ход, называется вторым. Они поменялись местами, значит, доказав, что у второго бесконечно много возможностей выиграть, мы доказываем, что у первого тоже бесконечно много таких возможностей.
Только вначале надо доказать про одного из них.

[ximikat]

Не знаю - будет ли это доказательством:
В том случае, когда, например, число заканчивается на $0$ или на $5$, то при этом условии второй всегда выигрывает. Например:
1. При $5$ 1-й ход $2^2$, второй $1$
2. При $10$ $2^2$, $2^2$, $1$, $1$,
3. При $15$: $3^3$, $2^2$, $1$, $1$
4. При $20$: $4^4$, $2^2$
5. При $25$ $4^4$, $3^3$
6. При $100$: $9^9$, $3^3$, $2^2$, $2^2$, $1$, $1$

Т.е. мы видим, что у того, кто ходит вторым всегда остаётся поле для манёвра и при этом он либо заканчивает свой ход так сказать контр-квадрадом, либо оставляет первому ходившему сделать ещё один ход. Последний же ход всегда в данном случае делает тот, кто может съесть число конфет в квадрате вторым ходом, либо четвёртым ходом, либо при остаче конфет меньше трёх оставить сопернику предпоследнюю конфету, а съесть последнюю.
А поскольку таких натуральных чисел, заканчивающихся на $0$ и на $5$ большое множество (а может быть и бесконечное не знаю), то наблюдаемая последовательность игры по съеданию конфет доказана.

[ИСН]

А если при 25 первый сделает ход $5^2$ - что тогда?

(Оффтоп)

Когда я учился играть в шахматы, меня тоже очень бесило, что противник делает не такие ходы, как надо (в смысле, как мне надо). Постоянно такая хрень. Плюнул в итоге на эту игру, ну её к чёрту.