Найти предел функции

[l0ki]

Здравствуйте, подскажите как решать задачу. Тут вроде все просто, но я давно это все проходил и про пределы не очень помню.
Найти предел функции:

$y=\frac{1}{3x-3}-\frac{3}{\ln x}$ при $x\to 1$

Тут неопределенность вида $\infty - \infty$, которую я никак не могу найти как раскрывать.

Я преобразовал в дробь, чтобы применить правило Лопиталя:

$\lim\limits_{x\to 1} {\frac{\ln x - 9(x-1)}{(3x-3)\ln x}} = \lim\limits_{x\to 1} {\frac{\frac{1}{x} - 9 }{3\ln x+\frac{3x}{x}+\frac{3}{x}}} = $

Дальше надо анализировать односторонние пределы или как?

[Joker_vD]

Нет. У вас внизу должно стоять $3\ln x+3-\frac3x$. Тогда предел равен бесконечности.

[ewert]

Во-первых, сделайте замену $x-1=t$. Во-вторых, после приведения к общему знаменателю перейдите в знаменателе к эквивалентному выражению. А дальше -- как хотите, можете и лопиталить, а можете и сразу ответ.

[l0ki]

PAV в сообщении #412453 писал(а):

используйте \ln для записи логарифма и других стандартных математических функций

Ок, буду.

Joker_vD в сообщении #412462 писал(а):

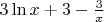
Нет. У вас внизу должно стоять . Тогда предел равен бесконечности.

Дада, там минус, я опечатался. Но я проверил пример на wolframalpha и он говорит, что при 1- получится $+\infty$, а при 1+ $-\infty$. И я теперь думаю как это проверить/доказать. Ведь если предел правый и левый разные, то это и надо указать в ответе, правильно?

ewert в сообщении #412465 писал(а):

Во-первых, сделайте замену $x-1=t$. Во-вторых, после приведения к общему знаменателю перейдите в знаменателе к эквивалентному выражению. А дальше -- как хотите, можете и лопиталить, а можете и сразу ответ.

У меня получилось как-то так:
$x-1 = t$,$x =1 + t$
$\lim\limits_{t\to 0} {\frac{\ln (t+1) - 9t} {3t\ln(t+1) } = \lim\limits_{t\to 0} {\frac { \frac{1}{t+1} - 9} {3\ln(t+1) + \frac{3t}{t+1} } = -\infty$

$x-1 = -t$,$x =1 - t$
$\lim\limits_{t\to 0} {\frac{\ln (1-t) + 9t} {-3t\ln(1-t) } = \lim\limits_{t\to 0} {\frac { \frac{1}{1-t} + 9} {-3\ln(1-t) - \frac{3t}{1-t} } = +\infty$

Правильно ли я решаю или надо как-то по-другому?

[ewert]

l0ki в сообщении #412493 писал(а):

Правильно ли я решаю

Правильно в принципе, но неразумно.

Во-первых, не надо делать двух разных замен (тем более что из-за этого Вы путаетесь в знаках при дифференцировании логарифмов). Зато надо было обязательно указать, к плюс нулю или к минус нулю стремится $t$. Во-вторых, следовало заменить логарифм в знаменателе на эквивалентное, чтобы не делать лишней работы.

[l0ki]

Я просто не понял сразу про эквивалентные выражения, т.к. вообще забыл что это)
Вот так более похоже на правду?

$x-1 = t \to x = t+1$
$\lim\limits_{t \to 0} {\frac{\ln (t+1) - 9t} {3t\ln(t+1) } =$
Эквивалентная замена: ln(1+t) = t
$\lim\limits_{t \to 0} {\frac{t - 9t} {3t^2 } = \lim\limits_{t \to 0} {\frac{ - 8t} {3t^2 } = \lim\limits_{t \to 0} {\frac{ - 8} {3t }$
$\lim\limits_{t^+ \to 0} {\frac{ - 8} {3t } = -\infty$
$\lim\limits_{t^- \to 0} {\frac{ - 8} {3t } = +\infty$

[ewert]

Только, во-первых, не $\ln(1+t)=t$, а $\ln(1+t)\sim t$. Во-вторых, не $t^+\to0$, а $t\to+0$. В-третьих, на эквивалентное можно заменять множители, но, вообще говоря, не слагаемые. А если заменять, то делать это осмысленно. В данном случае так:

$\dfrac{\ln(1+t)-9t}{3t\,\ln(1+t)}\sim\dfrac{\ln(1+t)-9t}{3t^2}=\dfrac{t(\frac{\ln(1+t)}{t}-9)}{3t^2}\sim\dfrac{t\cdot(-8)}{3t^2}\,.$

Последнее -- потому, что круглые скобки стремятся к конечному пределу. А вот если бы там получалась не восьмёрка, а ноль, то этот трюк не прошёл бы.

[l0ki]

Спасибо большое за пояснения, теперь все понятно. Я вспомнил теперь, что только в произведении эквивалентные заменяются. А про t+ это я описался, пока эту формулу набирал. Ну и равно вместо эквивалентно я необдуманно, конечно, воткнул.