Есть занумерованные ящики, в ящиках лежат черные и белые шары, причем в ящике с номером

лежит

белый и

черных шаров (в данном конкретном случае
![$f(n) = [\ln^2 n]$ $f(n) = [\ln^2 n]$](https://dxdy-01.korotkov.co.uk/f/8/1/f/81f4191f905d4946fba796c38d0cbfb082.png)
),
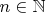
.
Опыт состоит во взятии из каждого ящика по одному шару, его исход — набор шаров. Его можно представлять как цепочку вида

, т.е. как функцию

. Тогда всего у нас имеется

исходов — и мы не можем использовать классическое определение вероятности. И пределы считать тоже не совсем понятно зачем — а ну как можно подобрать такую

, что указанный
Skipper'ом предел не будет существовать? Что тогда? "Нету вероятности"?
Ладно, насчет "не будет существовать" — это я погорячился. Для всех

таких, что

этот предел существует и равен нулю.



