Загадка ВТФ раскрыта?

[arseniiv]

(Оффтоп)

axtezius в сообщении #391601 писал(а):

Жду <…> комментарий

Комментарий — слово мужского рода.

[anwior]

axtezius в сообщении #391392 писал(а):

Привожу пример:
Таблица 1.
[url][URL=http://www.radikal.ru][/url][/url]

Словесную шелупонь вырезал, не моргнув ясными глазенками.
Из 60-ти числовых примеров по меньшей мере в 25-ти примерах автор
допустил ошибки в вычислениях.

Всё дерзать хотят голубчики, дерзать. Образованность всё хочут показать.
(А. Иванов)

[chulichkov2010]

Пермещено автором в другую тему

[bot]

chulichkov2010 в сообщении #392682 писал(а):

Я утверждал (а не утверждала), что сумма иррационального и целого есть иррациональное. Вы взяли два иррациональных.

Упрёк принимаю - действительно неверно прочитал.

(Оффтоп)

chulichkov2010 в сообщении #392682 писал(а):

У меня, кстати, сейчас глубокая ночь

Поэтому и отвечаете не в той теме?
А у меня, кстати (или, скорее, совсем некстати) приём зачётов у самых отборных кадров.

[axtezius]

axtezius в сообщении #391601 писал(а):

откуда ; ; .

-- Ср дек 29, 2010 13:38:18 --

Действительно, таблица для $\Delta = 5$ перевелась некорректно, правильно так:
[url][URL=http://www.radikal.ru][/url][/url]

Так же и здесь следует читать так:откуда $X =\sqrt{x^n}$; $Y=\sqrt{y^n}$; $Z=\sqrt{z^n}$

Лицо допустившее данные ошибки при публикации, строго наказано - встречу Нового года проведет на "сухом пайке".

Поздравляю всех с наступающим Новым годом, желаю всяческих успехов, любви и хорошего здоровья!!!

[axtezius]

Алгебраическое доказательство ВТФ.

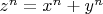
Великая теорема Ферма гласит: «Ни куб на два куба, ни квадрато – квадрат и вообще никакая, кроме квадрата, степень не может быть разложена на сумму двух таких же». Тем самым он утверждает, что при $n > 2$ выразить уравнение $z^n = x^n + y^n$ (1) в натуральных числах невозможно. После бесконечных неудачных попыток найти элементарное доказательство ВТФ сформировалось мнение, что П. Ферма сделав приписку к теореме: «Я нашел удивительное доказательство тому…» самоуверенно ошибся. 13 лет назад я задался вопросом, почему уравнение
$z^2 = x^2 + y^2$ имеет решение в натуральных числах. Однако, методы нахождения пифагоровых троек, предлагаемые современной теорией чисел, меня не устраивали, так как получаемые тройки между собой никак не были связаны, а потому никакой анализ их не был возможным. Однако известно, что сам Пифагор находил свои тройки посредством уравнения:

$$x=\frac{y^2-1}{2}$$

(2)

Вопрос: откуда он взял это уравнение? Впишем на радиус $R = z$ окружности прямоугольный треугольник OAB.
Рис. 1.

[url]URL=http://www.radikal.ru][/url][/url]

Данный прямоугольный треугольник соответствует первичной пифагоровой тройке $x = 4; y = 3; z = 5$. Поскольку $R = OA = (OB + BC)$, то $z = x + \Delta$.
Поскольку радиус окружности может принимать размерность от 1 до $\infty$, то и значения $x$ и $z$, могут принимать те же значения. Для любой окружности радиусом $R =z$, всегда $z = x+ \Delta$. При этом, если мы рассматриваем, что $x, y, z$ числа натуральные, то и значение $\Delta (0 < \Delta < z)$, всегда будет числом натуральным, что обеспечивает нахождение всего множества пифагоровых троек.
Представим уравнение

$$x^2 + y^2 = z^2$$

в виде

$$x^2+y^2=(x + \Delta)^2$$

преобразуя которое, получим:

$$x=\frac{y^2-\Delta^2}{2\Delta}$$

(3)
Отсюда видно, что при $\Delta = 1$, мы получим искомое уравнение Пифагора (1).
Значение $z$ будет:

$$z=\frac{y^2+\Delta^2}{2\Delta}$$

(4)
И тогда уравнение $x^2 + y^2 = z^2$
можно представить как:

$$A\left(\frac{y^2-\Delta^2}{2\Delta}\right)^2+By^2= C\left(\frac{y^2+\Delta^2}{2\Delta}\right)^2$$

(5)
Откуда

$$y=\sqrt{\Delta^2+2x\Delta}$$

или

$$y=\sqrt{(x+z)\Delta}$$

(6)

$$\Delta=\frac{y^2}{x+z}$$

(6*)
Тем самым неопределенное уравнение $z^2 = x^2 + y^2$ (7) становится вполне определяемым, где $z > x > y$; и $0 < \Delta < z$, и позволяет разложить любое значение $z^2$. Для разложения $z^2$ в натуральных числах, требуется, что бы значение $\Delta$ было так же числом натуральным.
Вернемся к свойствам самих пифагоровых троек, т. е. решениям уравнения (5). Поскольку подробный анализ свойств пифагоровых троек изложен в моей работе «Диалектика чисел», здесь я остановлюсь только на основных их свойствах. Точку A (рис. 1) с координатами $x, y$, (выраженную в натуральных числах, в данном случае 4; 3), назовем резонансной точкой. Данная точка расположена на эллиптической кривой $f(\Delta)$, отображающую уравнение (2). Каждому значению $\Delta$ соответствует своя эллиптическая кривая, на которой расположены все резонансные точки, определяемые уравнением (3). Для определения резонансных точек следует составлять таблицы соответствующие каждому значению $\Delta$ в отдельности (см. рис. 2).
Каждую такую последовательность резонансных точек я назвал дельта - функцией (\Deltaфункцией). Следует отметить, что не каждому натуральному значению $y$ соответствуют натуральные значения $x$, но, в любом случае, это есть решение прямоугольного треугольника. Если гипотенузу OA треугольника (рис. 1) продолжить в бесконечность, то на ней отложатся тройки, согласно уравнению $mz^2 = mx^2 + my^2$ (8). Причем, каждая такая тройка будет принадлежать своей и только своей - функции (эллиптической кривой) и потому никакие сокращения троек на НОД не допустимы.

Рис. 2.


[url][URL=http://www.radikal.ru][/url][/url]

Каждой примитивной (первообразной) тройке принадлежит свой прямоугольный треугольник и если их гипотенузы продолжить в бесконечность. То мы получим прямые, я назвал их вектор – тангенсоидами (V- тангенсоида), на которых будет расположено бесконечное множество производных троек согласно уравнению (8). Что отображено на рис. 3.

Рис. 3.

[url][URL=http://www.radikal.ru][/url][/url]

Следует отметить, что доказательство Великой теорема сделанное Эндрю Уайлсом в общем виде сводится к доказательству того, что пифагоровы тройки могут быть расположены только на эллиптических кривых. В свою очередь любая эллиптическая кривая принадлежит только квадратному уравнению. Только доказательство Э. Уайлсом осуществлено методом «спуска», а в «Диалектике чисел» доказывается то же самое, только методом «подъёма».
Таким образом, все пифагоровы тройки делятся на две группы:
- первообразные, (примитивные), не имеющие общего делителя;
- производные, имеющие наибольший общий делитель.
Кроме того, все пифагоровы тройки по своим свойствам подобны между собой и никаких исключений нет, и не может быть.
Если уравнение (8) представить в виде $Ax^2 + By^2 = Cz^2$ (9), то решение данного уравнения, как для прямоугольного треугольника возможно только в случае: $A = B = C = m$, и выражены они, должны быть, в натуральных числах. Причем, обязательным условием является:
$\Deltaz – x$, где $z > x > y$ (10).
В любом другом случае, это уже не будет решением прямоугольного треугольника.

Рис. 4.
[url][URL=http://www.radikal.ru][/url][/url]
Предположим, что на гипотенузе Z расположен квадрат площадью $z^2$ (см. рис. 4), который нам требуется разложить на два квадрата с площадями $x^n$ и $y^n$, и стороны которых $(X; Y; Z)$ выражены в натуральных числах.
Таким образом, мы должны решить задачу: возможно ли решить уравнение $x^n+y^n=z^n$ (11) в натуральных числах. Поскольку только их равенство позволит доказать неправомерность ВТФ.

Приведем данное уравнение к виду (9):
$x^{n-2}x^2+y^{n-2}y^2=z^{n-2}z^2$ или $Ax^2 + By^2 = Cz^2,
где: $A = x^{n-2}; B = y^{n-2}; C = z^{n-2}$; а квадраты $x^2; y^2; z^2$ есть единичные квадраты (на рис. 4 – квадраты красного цвета).
Вместо $x$ и $z$ подставим их значения согласно уравнениям (3), (4), которые являются единственно истинными для решения прямоугольного треугольника:

$$A\left(\frac{y^2-\Delta^2}{2\Delta}\right)^2+By^2= C\left(\frac{y^2+\Delta^2}{2\Delta}\right)^2$$

После возведения в степень и сокращений получим:

$$Ay^4+2Ay^2\Delta^2+A\Delta^4+4By^2\Delta^2= Cy^4+2Cy^2\Delta^2+C\Delta^4$$

$$y^4(A-C)+2y^2\Delta^2(2B-C-A)+\Delta^4(A-C)=0$$

$$(A-C)(y^4+\Delta^4)+2y^2\Delta^2(2B-C-A)=0$$

Таким образом, данное уравнение имеет решение относительно коэффициентов, только когда:
$( A - C) = -(2B - C - A)$ откуда $B = C$.
$(A – C) = 0$; откуда $A = C$.
$(2B – A – C) = 0$; откуда
$B=\frac{A+C}{2}$;
т. е. $C > A > B$.
Это следует понимать так, если мы имеем квадрат площадью $z^n$ и стороной, выраженной натуральным числом, то его можно разложить только на один квадрат площадью $x^n$ или $y^n$ со стороной выраженной натуральным числом. Сторона второго квадрата никогда натуральным числом выражена не будет.
И обратный вывод, если сложить два квадрата площадями $x^n$ и $y^n$, то сторона суммированного квадрата никогда не будет выражена натуральным числом. Придти к данному доказательству возможно только после детального изучения свойств пифагоровых чисел.
P.S. Вопрос: Достаточно ли было П. Ферма данного доказательства для вывода своей Великой теоремы.

[r-aax]

axtezius в сообщении #403744 писал(а):

Предположим, что на гипотенузе Z расположен квадрат площадью $z^2$ (см. рис. 4), который нам требуется разложить на два квадрата с площадями $x^n$ и $y^n$

Это описка?

axtezius в сообщении #403744 писал(а):

Приведем данное уравнение к виду (9):
$x^{n-2}x^2+y^{n-2}y^2=z^{n-2}z^2$ или $Ax^2 + By^2 = Cz^2,
где: $A = x^{n-2}; B = y^{n-2}; C = z^{n-2}$; а квадраты $x^2; y^2; z^2$ есть единичные квадраты (на рис. 4 – квадраты красного цвета).
Вместо $x$ и $z$ подставим их значения согласно уравнениям (3), (4), которые являются единственно истинными для решения прямоугольного треугольника:

$$A\left(\frac{y^2-\Delta^2}{2\Delta}\right)^2+By^2= C\left(\frac{y^2+\Delta^2}{2\Delta}\right)^2$$

С чего Вы взяли, что $x$ и $y$ являются решениями для прямоугольного треугольника?

[axtezius]

r-aax
Спасибо, действительно очипятка. Надо:$x^n$.

Цитата:

С чего Вы взяли, что и являются решениями для прямоугольного треугольника?

Из начальных условий и согласно рис. 4.

[Лукомор]

axtezius в сообщении #403744 писал(а):

Вопрос: Достаточно ли было П. Ферма данного доказательства для вывода своей Великой теоремы.

Ответ: Нет, не достаточно.
Рассмотрены лишь прямоугольные треугольники, а гипотетический треугольник, отвечающий уравнению Ферма,составленный из натуральных чисел, неизбежно будет остроугольным.

[r-aax]

axtezius в сообщении #405649 писал(а):

Цитата:

С чего Вы взяли, что и являются решениями для прямоугольного треугольника?

Из начальных условий и согласно рис. 4.

Таких начальных условий в ТФ нет.

Вы доказываете только то, что одновременно не могут выполняться два равенства: $x^2 + y^2 = z^2$ и $x^n + y^n = z^n$ для одних и тех же $x$, $y$ и $z$, но это и так очевидно.

[iakovlev]

"r-aax" - "браво"!
Вы явно делаете успехи.

[r-aax]

iakovlev в сообщении #405918 писал(а):

"r-aax" - "браво"!
Вы явно делаете успехи.

(Оффтоп)

У Вас ошибка так и осталась...

[axtezius]

Милые мои друзья – оппоненты, я над ВТФ работаю уже 13 лет и, естественно, что мне все понятно без каких-либо дополнительных пояснений. А, потому, сложилось мнение, что и другие поймут сразу все, что я хотел сказать. Ну и с опечатками та же история: когда одно и то же перепечатываешь помногу раз, уже допущенные ошибки просто не замечаешь, Уж не сердитесь на старика…
Ну а теперь позвольте закончить пояснения.

Рис. 1.

[url][URL=http://www.radikal.ru][/url][/url]

Самое главное, о чем все время забываю сказать. Обратимся к рис. 1, здесь видно, что графики уравнений (3), представляют собой эллиптические кривые, эксцентриситет которых, по мере удаления от центра координат, стремится к единице. Причем, каждому значению $\Delta$, соответствует своя эллиптическая кривая, по ветвям которой располагаются значения $z$, соответствующие значениям $\pm{y}$. Тем самым неопределенность значения $z^2=(x+yi)(x-yi)$ уже будет включена в уравнение (3). Таким образом, неопределенное уравнение $x^2+y^2=z^2$ в виде уравнения (5) становится конкретно определяемым.
Теперь предположим, что уравнение (1) имеет решение в натуральных числах, а это значит, что должно иметь место решение прямоугольного треугольника, $x^n+y^n=z^n$ аналогично решению $x^2+y^2=z^2$ (см. рис. 2), т. е. будем вести доказательство от противного.

Рис. 2.
[url][URL=http://www.radikal.ru][/url][/url]

Для доказательства построим единичный треугольник согласно условий рассмотренных выше. При этом возможны два варианта:
- Разложить квадрат площадью $z^n$ на два квадрата $x^n$ и $y^n$. Тогда по значению $z$ принимаем значение $\Delta$ и согласно условия $z>\Delta<x$, где $\Delta$ число натуральное, определяем $x$, а по уравнению $y=\sqrt{(x+z)\Delta}$, определим значение $y$.
- Обратное решение, сложить два квадрата площадями $x^n$ и $y^n$. Здесь значения $x$ и $y$ уже заданы и значение $z$ определяется из $z=\sqrt{x^2+y^2}$. В обоих случаях полученный треугольник $OCD$ будет прямоугольным. Это чисто гипотетический треугольник, т. е. мы, предполагаем, что он имеет решение в натуральных числах. Здесь следует сказать, что уже на этом этапе, если $\Delta$ выражено натуральным числом, разложить данный единичный треугольник в натуральных числах будет уже невозможно. Тем не менее, предположим обратное. Тогда при умножении значений $x; y; z$ на коэффициенты $A; B; C$, мы из треугольника OCD должны будем получить треугольник OAB, но это будет возможным только при равенстве коэффициентов $A=B=C$. Но поскольку, согласно произведенным вычислениям, такое равенство невозможно, следует, что теорема П. Ферма, справедлива.

[serval]

axtezius в сообщении #408567 писал(а):

я над ВТФ работаю уже 13 лет

А я 23. Или 24, уже не помню. И постоянно нахожу что-то новое.

[venco]

axtezius в сообщении #408567 писал(а):

Милые мои друзья – оппоненты, я над ВТФ работаю уже 13 лет и, естественно, что мне все понятно без каких-либо дополнительных пояснений.

Не похоже, что всё понятно.
Вам уже возразили:

r-aax в сообщении #405783 писал(а):

Вы доказываете только то, что одновременно не могут выполняться два равенства: $x^2 + y^2 = z^2$ и $x^n + y^n = z^n$ для одних и тех же $x$, $y$ и $z$, но это и так очевидно.