Опечатка в справочнике или моё непонимание?

[Caran-d'Ache]

Добрый день!
Столкнулся с такой проблемой. Для расчётов некоторых рядов пришлось воспользоваться набором справочников с таблицами рядов и интегралов от спецфункций. В частности один из необходимых мне результатов я обнаружил в справочнике Прудников А.П., Брычков Ю.А., Маричев О.И. - Интегралы и ряды. Том 2. Специальные функции, 2003 г.
Ряд выглядит следующим образом:
$\sum _{k=1}^{\infty } \frac{(-1)^k I_k(z)}{k^2}=\frac{1}{2} H_{-1,0}(z)-\frac{\frac{\partial I_{\nu }(z)}{\partial \nu }}{4}\right|_{\nu \to 0}-\frac{\pi ^2 I_0(z)}{12}$
На всякий случай, чтоб меня не заподозрили в круворукости и ошибках при наборе, прикладываю ссылку на фото со страницей из книги (глава 5, пункт 5.8.2 формула № 14, стр. 612):
http://img443.**invalid link**/f/p0612.png/
Вроде бы удобоваримый результат, но, переходя в конец справочника (стр. 658 той же книги) для определения функции $H_{-1,0}(z)$, я вижу следующее выражение:

$H_{\mu ,\nu }(z)=h_{\mu ,\nu }(z)-\frac{\sqrt{\pi } \Gamma (\mu -\nu +1) \Gamma (\mu +\nu +1) }{2^{\mu +1} \Gamma \left(\mu +\frac{3}{2}\right)}\left(\frac{K_{\nu }(z) \sin (\pi (\nu -\mu ))}{\pi \cos (\pi \mu )}+I_{\nu }(z)\right)$
$h_{\mu ,\nu }(z)=\frac{e^{-z} z^{\mu +1}}{(\mu +1)^2-\nu ^2}\, _2F_2\left(1,\mu +\frac{3}{2};\mu -\nu +2,\mu +\nu +2;2 z\right)$

В книге это выглядит вот так: http://img714.**invalid link**/i/p0658.png/

Ну и естественно, что подставляя сюда индексы $\mu=-1 ,\nu=0$ я получаю бесконечность... Вот незадача. Как это понимать. Означает ли это, что ряд расходится и сумму найти будет не возможно (и зачем тогда было приводить такой результат?) или я чего-то неверно понимаю?

P.S.: заранее извиняюсь перед модераторами, если сделал что-то не по правилам с сылками или картинками, но увы я не смог найти, как их можно включить в текст темы.

[ewert]

Caran-d'Ache в сообщении #399765 писал(а):

Ну и естественно, что подставляя сюда индексы $\mu=-1 ,\nu=0$ я получаю бесконечность...

Я в гипергеометрических функциях не разбираюсь, но: почему бы такой функции и не обратиться в ноль при указанных Вами параметрах?...

[Caran-d'Ache]

не, насколько мне известно при таких параметрах гипергеометрическая функция выродится в экспоненту с некоторым не нулевым множителем, так что тут всё нормально.
А вот знаменатель множителя перед гипергеометрической функцией обращается в бесконечность:
$\frac{1}{(\mu +1)^2-\nu ^2}\to \infty $ при $\mu=-1 ,\nu=0$.
А так же в формуле для $H_{\mu ,\nu }(z)$ во втором слагаемом получаем гамма-функции от нуля, что тоже, если мне память не изменяет, бесконечность.

[ewert]

Caran-d'Ache в сообщении #399811 писал(а):

во втором слагаемом получаем гамма-функции от нуля, что тоже, если мне память не изменяет, бесконечность.

Не изменяет. Ну видите, у Вас получается сумма двух каких-то бесконечностей, которая может дать что угодно, в т.ч. и конечное число.

[Caran-d'Ache]

эээ... кхм... спасибо, уже легче, т.е. это моё недопонимание.
Но всё же как мне найти результирующее число (если оно действительно получается), я же не могу просто так подставить индексы. Надо ли мне преобразовывать это как-то и совершать определённые предельные переходы или как-то ещё?
Мне в результате необходима функциональная зависимость от $z$, для её дальнейшего численного исследование (работаю преимущественно в Wolfram Mathematica, но она к сожалению упрощать выражение отказалась).
Ещё меня сильно интересует сумма ряда более общего вида:
$\sum _{k=1}^{\infty } \frac{(-1)^k \cos{2 k \phi} I_k(z)}{k^2}$
К сожалению по нему ничего пока не нашёл ни в одном справочнике. Сходится ли он и, если да, то чему равна сумма. Или хотя бы подскажите справочники по данным рядам (ряды по бесселевым функциям). Смотрел: Прудников-Брычков-Маричев (в различных комбинациях ;) и различных годов выпуска), Бейтман (несколько справочников), Ватсон, Янке-Эмде-Лёш, Абрамовиц-Стиган.

-- Пт янв 14, 2011 14:15:38 --

Сделал следующее:
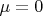
Положил $\mu=0$ и, предполагая, что $\nu$ целое, упростил, сгруппировал слагаемые и в итоге получил следующее выражение:

$H(z,\mu )=I_0(z) \left(\frac{z^{\mu +1}}{(\mu +1)^2}-\frac{\sqrt{\pi } \Gamma (\mu +1) \Gamma (\mu +1)}{2^{\mu +1} \Gamma \left(\mu +\frac{3}{2}\right)}\right)$.

Множитель с скобках и даёт бесконечность. К сожалению попытка взять в Математике предел этой функции при $\mu \to \infty$ привела к следующему ответу:
$\text{DirectedInfinity}\left[\log (z)+2 \gamma +\log (2)+\psi ^{(0)}\left(\frac{1}{2}\right)\right]$
Что как я понимаю эквивалентно просто бесконечности с некоторым знаком, определяемым значением аргумента. Но всё равно это бесконечность. Т.е. исходный ряд расходится? Тогда зачем было приводить этот результат в справочнике?

[Caran-d'Ache]

Извиняюсь за опечатку, предел брал конечно же при $\mu \to -1$

-- Пт янв 14, 2011 15:10:26 --

Для числителя
$f_{1}(\mu ,z)=(2 z)^{\mu +1} \Gamma \left(\mu +\frac{3}{2}\right)-\sqrt{\pi } ((\mu +1) \Gamma (\mu +1))^2$
И для знаменателя
$f_{2}(\mu ,z)=(\mu +1)^2 2^{\mu +1} \Gamma \left(\mu +\frac{3}{2}\right);$
После чего воспользовался правилом Лопиталя и дважды продифференцировал числитель и знаменатель.
И нашёл предел при $\mu \to -1$:
$\frac{1}{12} \left(6 \left(\log \left(\frac{z}{4}\right)-2 \gamma \right) \log (z)+\pi ^2+6 \log ^2(2)+6 \gamma (\log (4)-3 \gamma )\right)$

В итоге, в виде предела исходной функции получаю:
$\frac{1}{12} \left(6 \left(\log \left(\frac{z}{4}\right)-2 \gamma \right) \log (z)+\pi ^2+6 \log ^2(2)+6 \gamma (\log (4)-3 \gamma )\right) I_0(z)$
Корректно ли это?
Меня несколько настораживает, что результирующая функция для отрицательного аргумента даёт комплексные значения.

[Aleksandrito]

Извините что вмешиваюсь, тем более так поздно.
Имеется несколько замечаний к вашему представлению ряда.
Кстати очень простого и по моему если не подводит память для него есть более простое интегральное представление. (Что - т опохожее приходилось анализировать при решении ур- ний теплопроводности).
И ещё Для функций Ханкеля не видел более нигде такого представления.
Они определены Как первая и вторая Третьего рода с изменяющимся индексом.
У вас Индекс нулевой а функция как я понял -1 - мне это не понятно.
И ещё такое представление ф-ций Ханкеля напоминает ассимтотическое разложение. И это только на первй взгляд без особого сравнения .
Поэтому у меня вопрос насколько можно доверять вышеуказанной литературе?

[Caran-d'Ache]

На самом деле ещё ничего не поздно, т.к. итогового ответа, удовлетворяющего меня я пока не получил, хотя с исходным рядом вроде бы разобрался.
По поводу обозначений. Тут $H_{\mu ,\nu }(z)$ не функция Ханкеля (если бы это было так, то тут бы у меня проблем не было), это просто обозначение, для сокращения записи, как я понял.
По поводу доверия используемому справочнику (Прудников А.П., Брычков Ю.А., Маричев О.И. - Интегралы и ряды. Том 2. Специальные функции, 2003 г.) вот в этом и заключался исходный вопрос. Хотя если не доверять такой литературе, то не стоит доверять вообще ничему.
И, кстати, по поводу ряда. Для меня так ещё и остался открытым вопрос о сумме рядов вида $\sum _{k=1}^{\infty } \frac{(-1)^k \cos{2 k \phi} I_k(z)}{k^2}$ и $\sum _{k=1}^{\infty } \frac{(-1)^k \cos{(2 (k+1) \phi)} I_{k+1}(z)}{(k+1)^2}$. Такого в справочниках не нашёл. Буду очень благодарен за идею КАК...

[Aleksandrito]

Что касается второго ряда с косинусом, то посколку любые значения косинуса можно рассматривать как коэффициенты при ф-цях Бесселя, и учитывая свойство ограниченности косинуса сверху 1-цей, ряд мажорируем первым уже расмотренным рядом и в этом смысле он сходится если сходится первый ряд.

-- 19 янв 2011, 19:17 --

Да действительно посмотрел справочник всё именно так как и написано это обозначение.
И мне кажется что следующий раздел как раз о рядах с косинусом толи 5.8.3 толи 5.8.4
можно посмотреть.