Рассмотрим пространство

это, как известно, пространство Фреше.
Топология в нем задается полунормами

,

-- компакт.
Покажем, что ножество функций аналитичных хотя бы в одной точке интервала
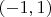
является множеством первой категории в

.
Введем обозначения

,
Через

обозначим множество функций, коэффициенты разложения Тейлора

которых в точке

оцениваются следующим образом:

Т.е. радиус сходимости ряда Тейлора не меньше чем

.
Легко проверить, что множества

замкнуты в

, и , что множество функций аналитичных хотя бы в одной точке иентервала
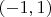
содержится в объединении множеств

.
Остается проверить что внутренность множеств

пуста. Действительно, пусть

.
Нужно для любого

и любых

предъявить функцию

такую, что

Выберем

так, что

.
Очевидно, достаточно взять

и подобрать малое

по

.