расшифруйте формулу

[guest001]

gris в сообщении #357128 писал(а):

В первом случае Вы считаете по формуле $\sum\limits_{i=1}^{3}\sum\limits_{j=1}^{2 } K_i_j$, то есть проверяете условие для $P_3_2$.

Во втором случае Вы считаете по формуле $\sum\limits_{j=1}^{3}\sum\limits_{i=1}^{2 } K_i_j$, то есть проверяете условие для $P_2_3$.

В первом случае суммирование идёт вдоль строк, во втором вдоль столбцов. В силу коммутативности и ассоциативности сложения мы получим одинаковый результат при симметричной матрице.
Ведь у Вас обсчитываются разные элементы:$P_2_3$ и $P_3_2$

Насчет 4 циклов - я примерно понял вашу идею т е $P_i_j $ждет во втором вложенном цикле пока не выполнится сумма элементов для $K_m_n$ и затем идет проверка в булевом операторе?
Это в смысле, чтобы все $P_i_j $ от 1 до M получили либо не получили значение 10 по проверке суммы K на "истина"?

-- Вт сен 28, 2010 23:07:39 --

А почему нельзя сразу просто подсчитать сумму по столбцам например и умножить её на 2, чтобы по рядам не считать? И уже это сравнить как (если сумма $\leq $3 например, то $P_i_j $=10)? Или есть особый момент?

-- Вт сен 28, 2010 23:26:06 --

под угловым движением подсчета суммы вы имеете ввиду что-то наподобие...



?

$P_i_j $сравнивается в процессе подсчета суммы (ряда/столбца) или в итоге подсчета суммы? Немного запутало описание вложенности вы его в примере

приравниваете к 10 в четвертом вложенном цикле значит как бы булев оператор срабатывает "в процессе" подсчета итоговой суммы? В смысле не когда сумма =90, а когда она в процессе получения этого числа.

-- Вт сен 28, 2010 23:41:54 --

Если предположить, что в процессе, то получается что-то в такой форме

Цитата:

сумма для $K_m_n$
и проверка в процессе получения итоговой суммы

итерация 1: (m=1; n=1 (по i)) (m=1; n=1 (по j))
$K_m_n:$=(1)+(1) $\leq$ 3 = истина
итерация 2: (m=2; n=1) (m=1; n=2)
$K_m_n:$=(1+2)+(1+4) $\leq$ 3 = ложь

одновременно нужно или по очереди?

[gris]

Я формулами задаю условие, а не описываю процесс решения.
Надо всегда начинать с ПЗ, то есть постановки задачи, и плавно переходить к ТЗ, то есть техническому заданию. Мы с Вами обсуждаем ТЗ, а ПЗ и в глаза не видели.
А начинать нужно с уяснения того, что нужно сделать.
Вообще есть понятие подматрицы. И мы ищем суммы элементов всех правоверхнеугловых подматриц. Их ровно столько, сколько элементов в исходной матрице. Каждому элементу соответствует одна такая подматрица. То есть такой аналог интегральной функции. Матрица, состоящая из сумм соответствующих угловых матриц, называется кумулятивной матрицей. Она имеет те же размеры. Пример:

$M: \qquad \left( \begin{array}{cccc} 1 & 2 & 0 & 0\\ 4 & 0& 0 & 3\\0 & 1 & 2 & 3\end {array} \right) $

$K(M): \left( \begin{array}{cccc} 1 & 2 & 2 & 2\\ 5 & 7& 7 & 10\\5 & 8 & 10 & 13\end {array} \right) $

Вы просто пытаетесь анализировать на ходу кумулятивную матрицу.
Вообще Вы затронули интереснейший аспект хранения данных. Ведь для каждой матрицы можно параллельно ей в тех же самых ячейках матрицы хранить и ей кумулянт.

Причём я знаю, почему они парой ходят .

[guest001]

Здорово :)

как математик, скажите правилен ли алгоритм для


как

Цитата:

сумма для $K_m_n$
и проверка в процессе получения итоговой суммы

шаг 1: (m=1; n=1 (по i)) (m=1; n=1 (по j))
$K_m_n$=(1)+(1) 3 = истина
шаг 2: (m=2; n=1) (m=1; n=2)
$K_m_n$=(1+2)+(1+4) 3 = ложь

на промежутке i=1: j=1 ?

или нужно по очереди двигаться и сравнивать в процессе накопления суммы.

Цитата:

Например если по m ,n++, то
1 $\leq$ 3 истина P_1_1 =10
1+2 $\leq$ 3 истина P_1_1 =10
3+3 $\leq$ 3 ложь
6+4 $\leq$ 3 ложь
10+5 $\leq$ 3 ложь
15 + 6 $\leq$ 3 ложь
21 + 7 $\leq$ 3 ложь
28 + 8 $\leq$ 3 ложь
36 + 9 $\leq$ 3 ложь

а затем по m++, n
45+1 $\leq$ 3 ложь
...

В самом процессе - это ведь разные числа получатся для $P_i_j$. Если считать
а) одновременно
в) по очереди


Ну или в зависимости от последовательности итератора сумм представленной формулы...
Я с удовольствием подсчитаю как угодно, хоть звездой, хоть углом или как только возможно, но мне нужно знать правильно ли я понимаю именно данную математическую инструкцию

-- Ср сен 29, 2010 00:45:35 --

Цитата:

Вы просто пытаетесь анализировать на ходу кумулятивную матрицу.
Вообще Вы затронули интереснейший аспект хранения данных. Ведь для каждой матрицы можно параллельно ей в тех же самых ячейках матрицы хранить и ей кумулянт.

Ну я понял по формуле, что так и нужно делать. Только не понял в какой последовательности?
Сначала пройтись по столбцам K, а потом по рядам K
И с процессе прохождения по столбцам а затем по рядам сравнивать кумулянт суммы с булевым условием?
или двигаться сразу в двух направлениях (как я описывал выше) и уже сравнивать кумулянт А+кумулянт В с булевым условием?
Вот это меня путает очень сильно. Помогите разобраться плз

-- Ср сен 29, 2010 00:51:30 --

Цитата:

Причём я знаю, почему они парой ходят

Здесь есть какой-то трюк ?

[guest001]

Ну со столбцами и рядами более понятно стало - спасибо, но вот как понимать параллельные суммы ?

Вот например

Есть матрица K
$K:= \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\7 & 8 & 9 \end{array} \right) $
$L:= \left( \begin{array}{ccc} 10 & 3 & 0 \end{array} \right) $
и есть формула например

$\sum_{i=1}^{M} L_i \sum_{j=1}^{N} K_i_j - (\sum_{i}^{M} \sum_{j}^{N} K_i_j +11) \leq 45$

То есть здесь нужно как-то параллельно двигаться, но только не пойму... В первом случае по строке, а во втором по столбцу или тоже по строке? Смущает то, что используются одни и те же итераторы для операций в теле цикла нескольких сумм

Помогите понять такую инструкцию плз

[gris]

Чуть поправлю
Есть матрица K и матрица $L$
$K:= \left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\7 & 8 & 9 \end{array} \right) $

$L:= \left( \begin{array}{ccc} 1 & 2 & 3\end{array} \right) $
и есть формула например

$\sum_{i=1}^{A} L_i \sum_{j=1}^{B} K_i_j - (\sum_{i=1}^{A} \sum_{j=1}^{B} K_i_j +11) \leqslant 45$

Несомненно, что на этапе препарации формула будет интерпретирована как

$\left(\sum\limits_{i=1}^{A} \left(L_i \sum\limits_{j=1}^{B} K_i_j \right) \right) - \left(\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \right) +11 \leqslant 45$
что, наверное, отличается от Вашего видения процесса. В этом случае никакого нарушения синтаксиса нет, ведь вложенности циклов с одинаковыми индексами суммирования нет. Если же Вы принудительно расставите скобки, чтобы была вложенность циклов, то препаратор просто сообщит об ошибке.
Формула может быть использована для проверки уcловия для вычисления какого-нибудь $C(A,B)$

[guest001]

Предположим условились, что матрица К имеет длину M x N, потому я не совсем понял...
Если учесть, что, дополню, условие гласит

$K_i_j =2$
если


В первой итерации это сумма по
1) первая сумма - это сумма первой строки
2) вторая сумма - это сумма первого столбца
итд
?

[gris]

Мs, похоже, говорим на разных языках.
Я, повторю, не сведущ в потенциально мёртвых языках программирования, поэтому некоторые конструкции и термины воспринимаю неправильно. Вы всё время говорите, что индекс суммирования это итератор. Для меня это весьма непривычно, потому что для итератора нельзя указывать границы изменения.
$\sum\limits_{i=1}^N k_i$ это обычная функция суммирования.
Итератор связан с определённой структурой и множество его значений определено локацией этой структуры. Например, если мы зададим конструкт $S$ для матрицы, определённый как её верхне-левая угловая подматрица, то условие, что суммы элементов этой подматрицы меньше соответствующих элементов другой матрицы запишется как

$\mathrm{for} \, S(P(N,M)) \quad\{\quad{\mathrm {if}\quad (\sum S(P(s))\leqslant A(s))\,\{K(s)=0\}\quad\mathrm {else}\,\{K(s)=1\}\quad\}$

Вы скажите определённо, чего Вы хотите. Если написать код на каком-то языке, то назовите язык и Вас проконсультируют знатоки этого языка. Если Вы пишете код для какого-то математического пакета, то скажите для какого.
Для меня Ваши задачи вполне понятны и я бы с удовольствием объяснил Вам их решение, да только не знаю, в каких терминах вести разговор. Использовать нотацию конструктов и итераторов мне кажется слишком снобистским для обычных матриц. Если бы это были графы, то куда ни шло. А для матриц обычное суммирование выше крыши. Но тогда уж не надо путаться в индексах.

[guest001]

Ну итерация в общем понятии - это просто шаг выполнения чего-либо :)

Спасибо, может термины где-то путались, но суть я понял примерно - это для меня самое главное.

Я как-то не нашел хорошего примера как умножают столбцы и ряды матрицы.

Например
Есть K (A x B)

$ K_i_j=5$
если
$\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \leq 10$

Получается нужно на первом шаге делать следующее?
1) K - Найти сумму столбца 1 (итерация 1)
2) K - Найти сумму ряда 1 (итерация 1)
3) Умножить сумма столбца 1 на сумма ряда 1 (итерация 1)
4) результат умножения (п.3) $\leq$ 10
5) $K_1_1$ равно/не равно 5

Если так, то действительно нужно 4 цикла, даже может 6 :)

[gris]

Если честно, то у меня какое-то подозрение закралось, что Вы просто нарочно это пишете. Если так, то это не очень вежливо с Вашей стороны и довольно обидно для того, кто старается объяснить Вам материал.
Надеюсь, однако, что я ошибаюсь, и Вы действительно хотите разобраться в программировании действий с матрицами.
В таком случае может быть и правда начать с более простых примеров: составить вектор из сумм по строкам, умножить матрицу на вектор, возвести квадратную матрицу в степень.
Я, наверное, плохо умею объяснять

-- Пт окт 01, 2010 00:00:46 --

[Maslov]

guest001 в сообщении #357808 писал(а):

Например
Есть K (A x B)

$ K_i_j=5$
если
$\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \leq 10$

guest001, я тут человек новый и многого не понимаю.

Так не сочтите за труд, объясните, пожалуйста, что означает вот это

guest001 в сообщении #357808 писал(а):

если
$\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \leq 10$

и откуда это взялось?
И как вообще это может быть, при условии, что все элементы матрицы K равны 5?
У Вас что, в матрице K может быть не больше двух элементов?

Может быть, это какая-нибудь задача? Тогда объясните, что дано и что требуется найти.

[guest001]

gris в сообщении #357811 писал(а):

Если честно, то у меня какое-то подозрение закралось, что Вы просто нарочно это пишете. Если так, то это не очень вежливо с Вашей стороны и довольно обидно для того, кто старается объяснить Вам материал.
Надеюсь, однако, что я ошибаюсь, и Вы действительно хотите разобраться в программировании действий с матрицами.
В таком случае может быть и правда начать с более простых примеров: составить вектор из сумм по строкам, умножить матрицу на вектор, возвести квадратную матрицу в степень.
Я, наверное, плохо умею объяснять

-- Пт окт 01, 2010 00:00:46 --

Нет, мне действительно не совсем понятны некоторые вещи. Вот например в последнем моем посте я просто хочу уже утвердиться, что понял манипуляции с матрицами и булевыми операторами. Мне интересно понять, как получать сумму ряда или столбца на заданном интервале i или j. То есть не как получать итог по завершению подсчета суммы, но брать например сумму ряда А и сумму столбца Б тут же производить с ними некоторые операции для возможно последующего анализа :)
Потому и спрашиваю насчет инструкции такого вида

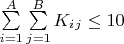
Это произведение столбца на ряд если А - это, так скажем, длина матрицы по Y, а В - длина матрицы по X?

Мне просто интересно покрутить этот рубик :)
Объясняете вы хорошо - мне нравится вас слушать. Если где-то произошло недоразумением, то я извиняюсь за может быть неверное изложение своих мыслей.

-- Пт окт 01, 2010 02:33:08 --

Maslov в сообщении #357823 писал(а):

guest001 в сообщении #357808 писал(а):

Например
Есть K (A x B)

$ K_i_j=5$
если
$\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \leq 10$

guest001, я тут человек новый и многого не понимаю.

Так не сочтите за труд, объясните, пожалуйста, что означает вот это

guest001 в сообщении #357808 писал(а):

если
$\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \leq 10$

и откуда это взялось?
И как вообще это может быть, при условии, что все элементы матрицы K равны 5?
У Вас что, в матрице K может быть не больше двух элементов?

Может быть, это какая-нибудь задача? Тогда объясните, что дано и что требуется найти.

Это не откуда не взялось, чтобы "задача" в смысле. Это возможный случай при том, что предел А - это не кол-во всех элементов матрицы, но кол-во элементов в пределах столбца (т е по Y и в данном примере равна 3). Соответственно В - это тоже длина, но уже ряда :) - все просто

И я думаю, что если имеем например матрицу К как (но на самом деле она может быть любой конечно же)
$K:=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right) $
и условие
$K_i_j = 5$ если
$\sum\limits_{i=1}^{A} \sum\limits_{j=1}^{B} K_i_j \leq 10$

то можно ли такой записью объяснить произведение столбца на ряд в пределах одной итерации, чтобы затем сравнивать значение как $\leq$ 10 ?
Полагаю, что действительно такая запись должна находится в теле второго вложенного цикла - это оптимально. Если тело второго цикла, то вышесказанное примерно так наверное должно выглядеть
$\left(i=1...A({j=1...B ({\sum\limits_{a=i}^{A} \sum\limits_{b=j}^{B} K_a_b \leq 10})})} \right) $
Я хочу понять правильно ли я понимаю данную инструкцию - все просто :)

[gris]

(Оффтоп)

Вчера вечером было осеннее, грустное настроение, а у Вас одни улыбочки в посте, похожие на ухмылочки. Вот мне и показалось, что Вы просто затеяли этот разговор ради лулзов, как это говорит некто мною весьма уважаемый, посылаю ему заодно луч симпатии. Так что прошу меня тоже простить за отсутствие чувства юмора по причине падающих с клёна листьев жёлтых в студёные лужи на мокром асфальте.

Математическая нотация подразумевает много умолчаний по свойству общепринятости. Читающий статью легко догадается о смысле формулы, исходя из контекста. Однако, если формулы приготовлены для автоматической обработки, скажем, интерпретатором или транскриптором, то эти умолчания могут сослужить плохую службу. Формула будет интерпретирована совсем не так, как Вы это задумали. Особенно это касается сумм. И особенно использования переменных суммирования или индексов, если хотите.

Я настоятельно советую не жалеть скобок при записи формул в непонятных и амбивалентных случаях и не обозначать различные индексы одной буквой. Да, в тексте это будет смотреться не очень, зато убережёт от неоднозначного понимания.

По общепринятому если после знака суммы стоит выражение, то действие знака распространяется до первого знак плюс или минус.

$\sum\limits_{i=1}^3a_i+b_j\to\left(\sum\limits_{i=1}^3a_i\right)+b_j=a_1+a_2+a_3+b_j$

Но! Если далее встречается выражение с индексом из знака суммы, то оно тоже включается в знак суммирования.

$\sum\limits_{i=1}^3b_j+a_i\to\sum\limits_{i=1}^3\left(b_j+a_i\right)=b_j+a_1+b_j+a_2+b_j+a_3$

В случае двойного знака суммирования он воспринимается как знак двойного суммирования:

$\sum\limits_{j=1}^2\sum\limits_{i=1}^3a_ib_j=a_1b_1+a_2b_1+a_3b_1+a_1b_2+a_2b_2+a_3b_2$

$\sum\limits_{j=1}^2\sum\limits_{i=1}^3a_j+b_i\to\sum\limits_{j=1}^2\left(\sum\limits_{i=1}^3\left(a_j+b_i\right)\right)=a_1+b_1+a_1+b_2+a_1+b_3+a_2+b_1+a_2+b_2+a_2+b_3$

$\sum\limits_{j=1}^2\sum\limits_{i=1}^3b_i+a_j\to\sum\limits_{j=1}^2\left(\left(\sum\limits_{i=1}^3b_i\right)+a_j\right)=b_1+b_2+b_3+a_1+b_1+b_2+b_3+a_2$

Как видите, от перестановки мест слагаемых сумма таки изменилась, как в условно сходящемся ряде.

Теперь насчёт индексов. Интерпретатор воспринимает букву индекса суммирования принадлежащей знаку суммирования в пределах его действия, даже если эта буква будет использована в качестве внешнего индекса. Даже если все индексы обозначить одной буквой, то интерпретатор просто заменит их на другие уже на этапе препарации. И формула будет транскрибирована в тот же си уже с изменёнными буквами (идентификаторами). Примеры интерпретации:

$\sum\limits_{i=1}^2\sum\limits_{i=1}^3a_ib_i\to\sum\limits_{i=1}^2\left(\sum\limits_{j=1}^3\left(a_jb_j\right)\right)=a_1b_1+a_2b_2+a_3b_3+a_1b_1+a_2b_2+a_3b_3$

$\sum\limits_{i=1}^2a_i\sum\limits_{i=1}^3b_i\to\sum\limits_{i=1}^2\left(a_i\left(\sum\limits_{j=1}^3b_j\right)\right)=a_1(b_1+b_2+b_3)+a_2(b_1+b_2+b_3)$

Кстати, это выражение с двойным суммированием может пониматься по разному:

$\sum\limits_{i=1}^2a_i\sum\limits_{i=1}^3b_i\to\left(\sum\limits_{i=1}^2a_i\right)\cdot\left(\sum\limits_{i=1}^3b_i\right)=(a_1+a_2)(b_1+b_2+b_3)$

что, как видите, моночленно с точностью до раскрытия скобок.

Итак, в Вашем выражении $K_i_j=\sum\limits_{i=1}^A\sum\limits_{j=1}^BK_i_j$ индексы в левом $K_i_j$ не имеют никакого отношения к правому $K_i_j$.

[guest001]

Вот это да... Я честно говоря подозревал, что привычные ab могу здесь иметь другое значение

Суммирование всех элементов


и произведение суммы А на сумму В


А если скобок нет. то есть просто
вот такая запись
$\sum\limits_{i}^{A} a_i \sum\limits_{j}^{B} a_j$

можно ли её интерпретировать к такому виду без потери сути инструкции?
$\sum\limits_{i}^{A} \sum\limits_{j}^{B} a_i_j$

или это всегда произведение суммы А на сумму В?

[gris]

В первом случае у Вас одномерный массив, в другом двумерный.
Это может быть "засчитано" если массив $a$ объявлен как двумерный. Тогда в случае написания записи с одним индексом интерпретатор считает индекс итератором по одномерной наложенной структуре.
Но этого лучше избегать.
К тому же такая запись совершенно недопустима в обычном тексте, статье.
Если Вы программируете с помощью интерпретатора, то знаете, что там можно задавать различные опции, и он всегда будет пытаться интерпретировать формулу, чтобы она стала синтаксически правильной. Но это часто приводит к совершенно неожидаемому результату.
Так что пишите аккуратно и в соответствии с общепринятыми стандартами.

[guest001]

Спасибо - интересно. С массивами я дело имею постоянно, но вот с именно матрицами в математическом понимании вопроса, то открыл для себя много нового
Учту все наставления. Спасибо всем

@gris

(Оффтоп)

Моя особая благодарность. Читая ваши посты, я больше и больше утверждаюсь, что вы в стоите рядах истинных служителей храма науки. Не могу выразить в двух словах тот положительный заряд, который производят на меня ваше терпение и внимательность. Одним словом - Браво!