Дополню ответ
AKM.

При прибавлении постоянной под знаком дифференциала, значение интеграла не изменяется, поэтому в моем предыдущем сообщении выражение для интеграла справедливо, как при
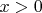
, так и при

.
На самом деле, полярная система координат к делу отношения не имеет.
1. Формула

легко может быть получена из геометрических соображений в частном случае, когда фигура является криволинейной трапецией «одновременно относительно осей
Ox и
Oy». Действительно, пусть криволинейная трапеция сначала ограничена снизу осью Ox, сверху

,

, тогда

. Пусть с другой стороны, криволинейная трапеция ограничена снизу осью
Oy, сверху

,

, тогда

. Складывая вмести эти два равенства, получим

. В рассматриваемом примере, кривая симметрична относительно обеих осей координат, поэтому достаточно вычислить площадь фигуры в первой четверти и умножить её на четыре; и, т.к. часть фигуры в первой четверти можно считать криволинейной трапецией как вида

,

, так и вида

, то

.
2. В данном случае, рассматривается площадь фигуры ограниченной
замкнутой линией, а потому формула

будет следствием формулы Грина, если выполнить интегрирование по замкнутой кривой, т.е., если

,

.



