(Оффтоп)
Перепишу то, что выше написал, без слов "гладкое многообразие" и "расслоение".
Любой вектор

,
приложенный к точке 
, является вектором скорости
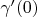
некоторой кривой

, для которой

.
Кривую можно "перенести" в

так:

и вычислить

-- вектор, приложенный в точке

Таким образом мы построили отображение

(первый множитель в прямом произведении -- множество точек, т.е. аффинное пространство, второй сомножитель - ассоциированное векторное)

(нетрудно доказать, что определение корректно, т.е. не зависит от выбора

)
Часто пишут

и называют это "дифференциал отображения

в точке

"
То, что дифференциалом называют отображение, а не его значение, диктуется принципиальным удобством, выражающемся, например, в цепном правиле:

В конце концов

-- это векторнозначная 1-форма, принимающая значения на векторных полях... она же производная по направлению, можно и точные 2-формы называть "производными в направлении бивекторов", но это извращение
Термин "производная" в многомерной ситуации встречается в виде "частной производной" и обобщающей ее "производной по направлению":

Но ведь это не что иное, как значение

!



