Решить в целых числах

[vbn]

В ходе геометрических построений возникла задача о решении в целых числах уравнения ($$a ,b, c, d, \beta \ne 0):

$$(a^2+\beta b^2)(c^2-d^2)=z^2.

Не знаю даже с чего начать. Буду благодарен за любые соображения.

[Руст]

vbn писал(а):

В ходе геометрических построений возникла задача о решении в целых числах уравнения ($$a ,b, c, d, \beta \ne 0):

$$(a^2+\beta b^2)(c^2-d^2)=z^2.

Не знаю даже с чего начать. Буду благодарен за любые соображения.

Если искать решения (возможно не все) разложите на две независимые системы:
$a^2+\beta b^2=z_1^2$, $c^2-d^2=z_2^2,$ $z=z_1z_2.$

[vbn]

Руст писал(а):

Если искать решения (возможно не все) разложите на две независимые системы:
$a^2+\beta b^2=z_1^2$, $c^2-d^2=z_2^2,$ $z=z_1z_2.$

Спасибо, Руст. Действительно, уравнение
$c^2-d^2=z_2^2,$ или $z_2^2+d^2=c^2,$
имеет бесконечно много решений (пифагоровы тройки).

Решением уравнения
$a^2+\beta b^2=z_1^2$ также являются пифагоровы тройки, если $\beta$ является полным квадратом.

В таком случае остается отыскать решения уравнения
$a^2+\beta b^2=z_1^2,$ где $\beta$ не является полным квадратом.

Возможно, это уравнение уже рассматривалось ранее, и решения его известны.
Буду признателен за ссылку на соответствующую литературу.

[Руст]

На второе уравнение можно смотреть как условие на норму алгебраического числа. Возьмите любой учебник по алгебраической теории чисел, и узнаете множество решений. Например Ленг "Алгебраические числа" или Боревич, Шафаревич "Теория чисел".

[vbn]

Скачал, наконец, Боревича, Шафаревича. Не осилил.
Благо, удалось найти решение уравнения
$a^2+\beta b^2=c^2$
с помощью элементарных методов, без использования алгебраической ТЧ,
у Серпинского - "О решении уравнений в целых числах", 1956.

[vbn]

Все те же геометрические построения привели к следующей задаче:
Доказать, что неполный квадрат разности не может быть равным полному квадрату, т.е., что уравнение
$$a^2 + b^2 - ab =c^2
не имеет решений в натуральных числах $$(a \ne b).

Вроде бы и сама формулировка говорит об этом: "неполный квадрат разности".
А как это показать, не знаю...

[незваный гость]

Ваше уравнение после умножения на 4 сводится к хорошо изученому: $x^2 + 3 y^2 = z^2$, где $x = 2a-b$, $y = b$, и $z = 2c$. Отсюда либо находятся решения, либо что их нет.

[Руст]

И без умножения, это общеизвестная вещь о единицах кольца $Z[w], w=e^{2\pi i/3},w^3=1.$

[vbn]

Так все-таки есть решения или нет

[Руст]

Если читали Шафаревича, то должны знать, что в кольце кругового расширения единицами являются только $\pm w^k, \ (w^n=1)$, что для вашего случая соответствует a=b.

[vbn]

Огромное спасибо, Руст!
А Шафаревича я, простите, не осилил

er писал(а):

Trueman писал(а):

А вот интересно, если взять треугольник с рациональными сторонами, найдётся ли у него внутренняя точка расстояния от которой до вершин треугольника будут рациональными?

Да, непонятно. Даже для равностороннего треугольника. Или для прямоугольного треугольника со сторонами 3,4,5.

http://dxdy.ru/viewtopic.php?p=15140#15140

Данная задача возникла в ходе поиска внутренней точки равностороннего треугольника с рациональными сторонами,
расстояние от которой до вершин треугольника также рационально.
Ответ — отрицательный.

Хотелось бы узнать, имеет ли этот результат сколь-нибудь значимую ценность?

[незваный гость]

Что-то уж больно просто у Вас получилось. По-моему, вопрос был открытым. Можно доказательство целиком (как Вы пришли к этому уравнению)?

[vbn]

Задача. Найти рациональные c, b, d такие, что и a — рационально.


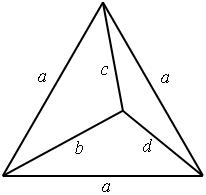
Воспользуемся теоремой косинусов:

$$ \left\{ \begin{array}{l} b^2=a^2+c^2-2ac \cos \widehat{a_l c};\\ d^2=a^2+c^2-2ac \cos \widehat{a_r c};\\ a^2=a^2+a^2-2aa \cos \widehat{a_l a_r}; \end{array}\right. \Rightarrow \left\{ \begin{array}{l} \cos \widehat{a_l c}=\frac {a^2+c^2-b^2} {2ac};\\ \\ \cos \widehat{a_r c}=\frac {a^2+c^2-d^2} {2ac};\\ \\ a^2=2a^2-2a^2 \cos (\widehat{a_l c}+\widehat{a_r c}); \end{array}\right. \Rightarrow \left\{ \begin{array}{l} \sin \widehat{a_l c}=\sqrt {1 - \left ( \frac {a^2+c^2-b^2} {2ac} \right )^2};\\ \\ \sin \widehat{a_r c}=\sqrt {1 - \left ( \frac {a^2+c^2-d^2} {2ac} \right )^2};\\ \\ a^2=2a^2-2a^2 \left [ \frac {a^2+c^2-b^2} {2ac} \frac {a^2+c^2-d^2} {2ac} - \sqrt {1 - \left ( \frac {a^2+c^2-b^2} {2ac} \right )^2} \sqrt {1 - \left ( \frac {a^2+c^2-d^2} {2ac} \right )^2}) \right ]. \end{array}\right$$

Раскрывая скобки в последнем уравнении системы, получаем:

$$a^2=\frac {b^2+d^2-c^2} {2} - \frac {a^4-a^2e^2-a^2d^2+b^2e^2} {2c^2}+ $+$$\frac {\sqrt {[4a^2c^2-(a^2+c^2-b^2)^2][4a^2c^2-(a^2+c^2-d^2)^2]}} {2c^2}. $$

Помножим каждую строну рассматриваемых треугольников на рациональную дробь $$c^{-1}
(используем свойство гомотетии), тогда необходимо найти такие рациональные a, b, d, что

$$\sqrt {[4a^2-(a^2+1-b^2)^2][4a^2-(a^2+1-d^2)^2]}=(a^4+1)-b^2(a^2+1-d^2)-d^2(a^2+1-b^2)-b^2e^2. $$

Положим далее

$$a^2=A, b^2=B, d^2=D,$$

тогда

$$\sqrt {[4A-(A+1-B)^2][4A-(A+1-D)^2]}=(A^2+1)-B(A+1-D)-D(A+1-B)-DE. $$

Положим, наконец,

$$\left\{ \begin{array}{l} A+1-B=u;\\ A+1-D=v; \end{array}\right. \Rightarrow \left\{ \begin{array}{l} B=A+1-u;\\ D=A+1-v, \end{array}\right. (1)$$

тогда

$$ \sqrt {(4A-u^2)(4A-v^2)}=uv-2A. $$

Возводя в квадрат, получаем:

$$ A= \frac {u^2+v^2-uv} {3}. $$

Пусть

$$a=\frac {p_a} {q_a}, u=\frac {p_u} {q_u}, v=\frac {p_v} {q_v}$$

где

$$p, q$$

— натуральные числа, тогда

$$Aq_u^2q_v^2=\frac {p_a^2}{q_a^2} q_u^2q_v^2=\frac {p_u^2q_v^2+p_v^2q+u^2-p_up_vq_uq_v} {3}.$$

Положим теперь

$$p_uq_v=\alpha, p_vq_u=\beta, aq_uq_v=\gamma$$

, тогда

$$\alpha^2 + \beta^2 - \alpha \beta=3\gamma^2.$$

Здесь

$$\alpha, \beta, \gamma$$

— натуральные числа.
Положим

$$x=\frac {2\alpha-\beta}{3}, y=\beta, z=2\gamma,$$

тогда

$$\alpha=\frac {3x+y}{2}$$

и

$$3x^2+y^2=z^2$$

.
Данное уравнение имеет решения, когда x — нечетное и

$$y=\frac{3x^2-1}{2}, z=\frac{3x^2+1}{2}.$$

Таким образом,

$$\alpha=\frac{3x+y}{2}=\frac{3x^2+6x-1}{4}, \beta=\frac{3x^2-1}{2}, \gamma=\frac{3x^2+1}{4},$$

значит

$$ \left\{ \begin{array}{l} p_uq_v=\frac {3x^2+6x-1}{4};\\ p_vq_u=\frac{3x^2-1}{2};\\ 2aq_uq_v={3x^2+1}{2}. \end{array}\right.$$

Отсюда следует, что числа

$$p_vq_u$$

и

$$2aq_u_qv$$

взаимно просты, так как разность между ними равна 1, следовательно,

$$q_u=1, u=p_u, p_v=\frac{3x^2-1}{2}.$$

Из первого и третьего уравнений системы следует соответственно, что u и a — натуральные числа, а из первого уравнения системы (1), что b — натуральное.
Таким образом, мы пришли к решению уравнения

$$a^2-b^2=u-1$$

в натуральных числах. Запишем его в виде

$$(u-1)g^2+b^2=a^2,$$

где g=1, тогда решением уравнения будет

$$g=1, b=\frac {u-1}{2}, a=\frac{u}{2}.$$

Итак,

$$u=p_u=\frac{1}{q_v} \frac{3x^2+6x-1}{4}=\frac{1}{ \frac{3x^2+1}{4a} } \frac{3x^2+6x-1}{4}=a\frac{3x^2+6x-1}{3x^2+1}=2a,$$

значит

$$\frac{3x^2+6x-1}{3x^2+1}=2,$$

откуда

$$x=1,$$

следовательно,

$$ \left\{ \begin{array}{l} b=a-1;\\ d^2=a^2-a+1=\left ( a-1 \right ) ^2 + \frac{3}{4};\\ \end{array}\right. \Rightarrow (2e)^2-(2a-1)^2=3 \Rightarrow \left\{ \begin{array}{l} a=1;\\ b=0;\\ d=1,\\ \end{array}\right. $$

что невозможно.
Решений нет.

[незваный гость]

vbn писал(а):

Данное уравнение имеет решения,

Вы уверены, что перебрали здесь все решения? Мне подозрительно.

Ваши выкладки до этой точки весьма правдоподобны, но без точного описания всех решений становится плохо.

Я, кажется, погорячился, сказав, что вопрос открыт. Задача о рациональных расстояниях, похоже, продолжает развлекать народ, и есть свежие результаты.

P.S. (от модератора). Форум не справляется с загрузкой картинок с narod.ru. Лучший вариант — поместить ее на http://imageshack.net. Этот сайт, кстати, предлагает и готовый код для вставки картинки на форуме.

Добавлено спустя 2 часа 56 минут 52 секунды:


Не пытайтесь доказать невозможное: в единичном правильном треугольнике есть точка с с расстояниями до вершин $(\frac{57}{112}, \frac{65}{112},\frac{73}{112})$. Эрик В. утверждает, что их бесконечно много, и я ему верю.

[незваный гость]

Post scriptum: quod vide A061281.