Задача. Найти рациональные c, b, d такие, что и a — рационально.
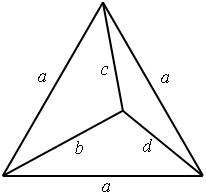
Воспользуемся теоремой косинусов:
![$$
\left\{ \begin{array}{l}
b^2=a^2+c^2-2ac \cos \widehat{a_l c};\\
d^2=a^2+c^2-2ac \cos \widehat{a_r c};\\
a^2=a^2+a^2-2aa \cos \widehat{a_l a_r};
\end{array}\right. \Rightarrow
\left\{ \begin{array}{l}
\cos \widehat{a_l c}=\frac {a^2+c^2-b^2} {2ac};\\
\\
\cos \widehat{a_r c}=\frac {a^2+c^2-d^2} {2ac};\\
\\
a^2=2a^2-2a^2 \cos (\widehat{a_l c}+\widehat{a_r c});
\end{array}\right. \Rightarrow
\left\{ \begin{array}{l}
\sin \widehat{a_l c}=\sqrt {1 - \left ( \frac {a^2+c^2-b^2} {2ac} \right )^2};\\
\\
\sin \widehat{a_r c}=\sqrt {1 - \left ( \frac {a^2+c^2-d^2} {2ac} \right )^2};\\
\\
a^2=2a^2-2a^2 \left [ \frac {a^2+c^2-b^2} {2ac} \frac {a^2+c^2-d^2} {2ac} - \sqrt {1 - \left ( \frac {a^2+c^2-b^2} {2ac} \right )^2} \sqrt {1 - \left ( \frac {a^2+c^2-d^2} {2ac} \right )^2})
\right ].
\end{array}\right$$ $$
\left\{ \begin{array}{l}
b^2=a^2+c^2-2ac \cos \widehat{a_l c};\\
d^2=a^2+c^2-2ac \cos \widehat{a_r c};\\
a^2=a^2+a^2-2aa \cos \widehat{a_l a_r};
\end{array}\right. \Rightarrow
\left\{ \begin{array}{l}
\cos \widehat{a_l c}=\frac {a^2+c^2-b^2} {2ac};\\
\\
\cos \widehat{a_r c}=\frac {a^2+c^2-d^2} {2ac};\\
\\
a^2=2a^2-2a^2 \cos (\widehat{a_l c}+\widehat{a_r c});
\end{array}\right. \Rightarrow
\left\{ \begin{array}{l}
\sin \widehat{a_l c}=\sqrt {1 - \left ( \frac {a^2+c^2-b^2} {2ac} \right )^2};\\
\\
\sin \widehat{a_r c}=\sqrt {1 - \left ( \frac {a^2+c^2-d^2} {2ac} \right )^2};\\
\\
a^2=2a^2-2a^2 \left [ \frac {a^2+c^2-b^2} {2ac} \frac {a^2+c^2-d^2} {2ac} - \sqrt {1 - \left ( \frac {a^2+c^2-b^2} {2ac} \right )^2} \sqrt {1 - \left ( \frac {a^2+c^2-d^2} {2ac} \right )^2})
\right ].
\end{array}\right$$](https://dxdy-03.korotkov.co.uk/f/6/a/9/6a96e65b8855c52f65232b0207e83c9c82.png)
Раскрывая скобки в последнем уравнении системы, получаем:
![$$a^2=\frac {b^2+d^2-c^2} {2} - \frac {a^4-a^2e^2-a^2d^2+b^2e^2} {2c^2}+
$+$$\frac {\sqrt {[4a^2c^2-(a^2+c^2-b^2)^2][4a^2c^2-(a^2+c^2-d^2)^2]}} {2c^2}.
$$ $$a^2=\frac {b^2+d^2-c^2} {2} - \frac {a^4-a^2e^2-a^2d^2+b^2e^2} {2c^2}+
$+$$\frac {\sqrt {[4a^2c^2-(a^2+c^2-b^2)^2][4a^2c^2-(a^2+c^2-d^2)^2]}} {2c^2}.
$$](https://dxdy-04.korotkov.co.uk/f/f/1/8/f18be053faf6a8a1ae07e709e272418e82.png)
Помножим каждую строну рассматриваемых треугольников на рациональную дробь

(используем свойство гомотетии), тогда необходимо найти такие рациональные a, b, d, что
![$$\sqrt {[4a^2-(a^2+1-b^2)^2][4a^2-(a^2+1-d^2)^2]}=(a^4+1)-b^2(a^2+1-d^2)-d^2(a^2+1-b^2)-b^2e^2.
$$ $$\sqrt {[4a^2-(a^2+1-b^2)^2][4a^2-(a^2+1-d^2)^2]}=(a^4+1)-b^2(a^2+1-d^2)-d^2(a^2+1-b^2)-b^2e^2.
$$](https://dxdy-02.korotkov.co.uk/f/1/4/5/145500243d799e49ec1d85418dd3c38b82.png)
Положим далее

тогда
![$$\sqrt {[4A-(A+1-B)^2][4A-(A+1-D)^2]}=(A^2+1)-B(A+1-D)-D(A+1-B)-DE.
$$ $$\sqrt {[4A-(A+1-B)^2][4A-(A+1-D)^2]}=(A^2+1)-B(A+1-D)-D(A+1-B)-DE.
$$](https://dxdy-01.korotkov.co.uk/f/8/3/d/83d541b234bd22d64f1b8520823569c482.png)
Положим, наконец,

тогда

Возводя в квадрат, получаем:

Пусть

где

— натуральные числа, тогда

Положим теперь

, тогда

Здесь

— натуральные числа.
Положим

тогда

и

.
Данное уравнение имеет решения, когда x — нечетное и

Таким образом,

значит

Отсюда следует, что числа

и

взаимно просты, так как разность между ними равна 1, следовательно,

Из первого и третьего уравнений системы следует соответственно, что u и a — натуральные числа, а из первого уравнения системы (1), что b — натуральное.
Таким образом, мы пришли к решению уравнения

в натуральных числах. Запишем его в виде

где g=1, тогда решением уравнения будет

Итак,

значит

откуда

следовательно,

что невозможно.
Решений нет.