Магические квадраты

[Nataly-Mak]

Программа на Бейсике готова. Протестировала, получила новый (оригинальный) пандиагональный квадрат из того же массива проcтых чисел, потому что здесь совсем другая структура квадрата:

7 101 271 307 167
181 337 107 97 131
197 127 41 211 277
71 151 367 227 37
397 137 67 11 241

Этот пандиагональный квадрат найден за 8 минут (на компилируемом Бейсике).

Заодно добавляю в "копилку" соответствующую перестановку из индексов элементов массива, авось пригодится:

1 8 20 22 14
15 23 9 7 11
16 10 4 17 21
6 13 24 18 3
25 12 5 2 19

Очень неудобно опять просить ice00 переписывать программу на C++
Поэтому сейчас попытаюсь сама переписать (по тому тексту, который мне прислал ice00 для предыдущей программы; программы эти очень похожи).
Если перепишу, тогда попрошу его сделать исполняемую программу по моему тексту. Во так, глядишь, плавно перейду на C++

Кто готов помочь?
Текст программы на Бейсике здесь:

(Оффтоп)

10 DIM A(5, 5), B(25), C(25)
12 OPEN "MK2.txt" FOR INPUT AS #1
14 FOR I = 1 TO 25: INPUT #1, C(I): NEXT I
15 CLOSE #1
16 S = 0
18 FOR I = 1 TO 25: S = S + C(I): NEXT I
20 S = S / 5: PRINT S: PRINT
22 IF INT(S) <> S THEN PRINT "OSHIBKA MASSIVA": GOTO 600
30 OPEN "MK10.txt" FOR OUTPUT AS #1
40 A(1, 1) = C(1): B(1) = C(1): Z = C(1): W = C(25)
42 FOR I = 2 TO 25
43 PRINT "I="; I
44 FOR J = 2 TO 25
45 PRINT "J="; J
46 IF J = I THEN 525
48 FOR K = 2 TO 25
50 IF K <> I THEN IF K <> J THEN 54
52 GOTO 520
54 FOR L = 2 TO 25
56 IF L <> I THEN IF L <> J THEN IF L <> K THEN 60
58 GOTO 515
60 B(2) = C(I): B(3) = C(J): B(4) = C(K): B(5) = C(L)
62 A(5, 1) = S - B(2) - B(3) - B(4) - B(5)
64 IF A(5, 1) < Z THEN 515
65 IF A(5, 1) > W THEN 515
66 FOR T = 1 TO 5
68 IF A(5, 1) = B(T) THEN 515
70 NEXT T
72 FOR T = 2 TO 25
74 IF A(5, 1) = C(T) THEN 80
76 NEXT T
78 GOTO 515
80 B(6) = A(5, 1)
82 FOR M = 2 TO 25
84 FOR T = 1 TO 6
86 IF C(M) = B(T) THEN 510
88 NEXT T
90 B(7) = C(M)
92 FOR N = 2 TO 25
94 FOR T = 1 TO 7
96 IF C(N) = B(T) THEN 505
98 NEXT T
100 B(8) = C(N)
102 FOR O = 2 TO 25
104 FOR T = 1 TO 8
106 IF C(O) = B(T) THEN 500
108 NEXT T
110 B(9) = C(O)
112 A(1, 2) = B(5) - B(9) + B(2)
114 IF A(1, 2) < Z THEN 500
116 IF A(1, 2) > W THEN 500
118 FOR T = 1 TO 9
120 IF A(1, 2) = B(T) THEN 500
122 NEXT T
124 FOR T = 2 TO 25
126 IF A(1, 2) = C(T) THEN 132
128 NEXT T
130 GOTO 500
132 B(10) = A(1, 2)
134 A(1, 3) = S - B(4) - B(8) - B(5) + B(9) - B(3) - B(2)
136 IF A(1, 3) < Z THEN 500
138 IF A(1, 3) > W THEN 500
140 FOR T = 1 TO 10
142 IF A(1, 3) = B(T) THEN 500
144 NEXT T
146 FOR T = 2 TO 25
148 IF A(1, 3) = C(T) THEN 154
150 NEXT T
152 GOTO 500
154 B(11) = A(1, 3)
156 A(1, 4) = B(8) + B(3) - B(7)
158 IF A(1, 4) < Z THEN 500
160 IF A(1, 4) > W THEN 500
162 FOR T = 1 TO 11
164 IF A(1, 4) = B(T) THEN 500
166 NEXT T
168 FOR T = 2 TO 25
170 IF A(1, 4) = C(T) THEN 176
172 NEXT T
174 GOTO 500
176 B(12) = A(1, 4)
178 A(1, 5) = B(4) - B(1) + B(7)
180 IF A(1, 5) < Z THEN 500
182 IF A(1, 5) > W THEN 500
184 FOR T = 1 TO 12
186 IF A(1, 5) = B(T) THEN 500
188 NEXT T
190 FOR T = 2 TO 25
192 IF A(1, 5) = C(T) THEN 198
194 NEXT T
196 GOTO 500
198 B(13) = A(1, 5)
200 A(2, 1) = B(9) + B(3) - B(7)
202 IF A(2, 1) < Z THEN 500
204 IF A(2, 1) > W THEN 500
206 FOR T = 1 TO 13
208 IF A(2, 1) = B(T) THEN 500
210 NEXT T
212 FOR T = 2 TO 25
214 IF A(2, 1) = C(T) THEN 220
216 NEXT T
218 GOTO 500
220 B(14) = A(2, 1)
222 A(2, 2) = B(4) + B(8) - B(1)
224 IF A(2, 2) < Z THEN 500
226 IF A(2, 2) > W THEN 500
228 FOR T = 1 TO 14
230 IF A(2, 2) = B(T) THEN 500
232 NEXT T
234 FOR T = 2 TO 25
236 IF A(2, 2) = C(T) THEN 242
238 NEXT T
240 GOTO 500
242 B(15) = A(2, 2)
244 A(2, 4) = B(1) + B(5) - B(9)
246 IF A(2, 4) < Z THEN 500
248 IF A(2, 4) > W THEN 500
250 FOR T = 1 TO 15
252 IF A(2, 4) = B(T) THEN 500
254 NEXT T
256 FOR T = 2 TO 25
258 IF A(2, 4) = C(T) THEN 264
260 NEXT T
262 GOTO 500
264 B(16) = A(2, 4)
266 A(2, 5) = S - B(4) - B(8) - B(5) - B(3)
268 IF A(2, 5) < Z THEN 500
270 IF A(2, 5) > W THEN 500
272 FOR T = 1 TO 16
274 IF A(2, 5) = B(T) THEN 500
276 NEXT T
278 FOR T = 2 TO 25
280 IF A(2, 5) = C(T) THEN 286
282 NEXT T
284 GOTO 500
286 B(17) = A(2, 5)
288 A(3, 1) = B(5) + B(7) - B(9)
290 IF A(3, 1) < Z THEN 500
292 IF A(3, 1) > W THEN 500
294 FOR T = 1 TO 17
296 IF A(3, 1) = B(T) THEN 500
298 NEXT T
300 FOR T = 2 TO 25
302 IF A(3, 1) = C(T) THEN 308
304 NEXT T
306 GOTO 500
308 B(18) = A(3, 1)
310 A(3, 2) = S - B(3) - B(2) - B(4) - B(8) - B(5) + B(1)
312 IF A(3, 2) < Z THEN 500
314 IF A(3, 2) > W THEN 500
316 FOR T = 1 TO 18
318 IF A(3, 2) = B(T) THEN 500
320 NEXT T
322 FOR T = 2 TO 25
324 IF A(3, 2) = C(T) THEN 330
326 NEXT T
328 GOTO 500
330 B(19) = A(3, 2)
332 A(3, 3) = B(3) + B(2) - B(7)
334 IF A(3, 3) < Z THEN 500
336 IF A(3, 3) > W THEN 500
338 FOR T = 1 TO 19
340 IF A(3, 3) = B(T) THEN 500
342 NEXT T
344 FOR T = 2 TO 25
346 IF A(3, 3) = C(T) THEN 352
348 NEXT T
350 GOTO 500
352 B(20) = A(3, 3)
354 A(3, 4) = B(9) - B(1) + B(4)
356 IF A(3, 4) < Z THEN 500
358 IF A(3, 4) > W THEN 500
360 FOR T = 1 TO 20
362 IF A(3, 4) = B(T) THEN 500
364 NEXT T
366 FOR T = 2 TO 25
368 IF A(3, 4) = C(T) THEN 374
370 NEXT T
372 GOTO 500
374 B(21) = A(3, 4)
376 A(4, 1) = B(2) + B(4) - B(1)
378 IF A(4, 1) < Z THEN 500
380 IF A(4, 1) > W THEN 500
382 FOR T = 1 TO 21
384 IF A(4, 1) = B(T) THEN 500
386 NEXT T
388 FOR T = 2 TO 25
390 IF A(4, 1) = C(T) THEN 396
392 NEXT T
394 GOTO 500
396 B(22) = A(4, 1)
398 A(4, 3) = B(8) + B(5) - B(9)
400 IF A(4, 3) < Z THEN 500
402 IF A(4, 3) > W THEN 500
404 FOR T = 1 TO 22
406 IF A(4, 3) = B(T) THEN 500
408 NEXT T
410 FOR T = 2 TO 25
412 IF A(4, 3) = C(T) THEN 418
414 NEXT T
416 GOTO 500
418 B(23) = A(4, 3)
420 A(4, 4) = S - B(3) - B(2) - B(4) - B(8) - B(5) + B(7)
422 IF A(4, 4) < Z THEN 500
424 IF A(4, 4) > W THEN 500
426 FOR T = 1 TO 23
428 IF A(4, 4) = B(T) THEN 500
430 NEXT T
432 FOR T = 2 TO 25
434 IF A(4, 4) = C(T) THEN 440
436 NEXT T
438 GOTO 500
440 B(24) = A(4, 4)
442 A(4, 5) = B(3) + B(1) - B(7)
444 IF A(4, 5) < Z THEN 500
446 IF A(4, 5) > W THEN 500
448 FOR T = 1 TO 24
450 IF A(4, 5) = B(T) THEN 500
452 NEXT T
454 FOR T = 2 TO 25
456 IF A(4, 5) = C(T) THEN 462
458 NEXT T
460 GOTO 500
462 B(25) = A(4, 5)
470 A(2, 3) = B(7): A(3, 5) = B(8): A(4, 2) = B(9)
472 A(5, 2) = B(3): A(5, 3) = B(4): A(5, 4) = B(2): A(5, 5) = B(5)
474 FOR T = 1 TO 5
476 FOR R = 1 TO 5
478 PRINT A(T, R);
480 PRINT #1, A(T, R);
482 NEXT R
484 PRINT : PRINT #1,
486 NEXT T
488 PRINT : PRINT #1,
490 GOTO 600
500 NEXT O
505 NEXT N
510 NEXT M
515 NEXT L
520 NEXT K
525 NEXT J
530 NEXT I
600 PRINT : PRINT "KONEC PROGRAMMY": PRINT
610 END

Программа работает до первого найденного квадрата. Однако если выбросить строку
490 GOTO 600
то будут построены все квадраты (с учётом параллельного переноса на торе).

Пошла осваивать C++

[ice00]

Цитата:

Пошла осваивать C++

C++ is a structured language so the use of GOTO instruction is not so good. This is why I insertd the 'continue' instruction that performe a sort of goto after the last instruction inside the cycle. 'continue' and 'brack' can be used inside loops to have the equivalent of a Goto.

However, I left in code some Goto as it need lot of time to rewrite it without the use of Goto. The result will be a full structure source code easy to understand and follow, but as soos as this program just need to be the equivalent of Basic code, it can be good enought.

For me, the translation of the new Basic source to C++ will require to attend the next weekend, cannon do it before :(

However this night I sent you the full C++ source of previous program (so you can share it for the one that want to code) that contains all the routines for read sequences from files and the other controls around.

[Nataly-Mak]

ice00
спасибо, но плохо получился перевод и не всё поняла.
Начала переписывать программу и вскоре затормозила, потому что никак не понимаю действие условного оператора. И много ещё непонятного. Короче, переписать по образцу текста с ходу не получилось. Язык Бейсик, наверное, самый простой язык.
Вот, например, цикл на Бейсике:

for i=1 to 25

вы пишете так:

for (int i=0; i<24; i++)

Это мне понятно.
Но вот в другом месте на Бейсике:

for j=2 to 25

вы пишете:

for (int j=1; j<25; j++)

И я уже в тупике. Почему здесь j<25, а в предыдущем цикле i<24, хотя в обоих цикла последнее значение переменной цикла равно 25?

Одним словом, освоение C++ откладывается.
Буду гонять программу на Бейсике. Она стала работать намного быстрее предыдущего варианта.
Помочь, к сожалению, кроме вас, некому

[ice00]

Цитата:

for i=1 to 25

вы пишете так:

for (int i=0; i<24; i++)

If you see the above, then it is a wrong conversion.

See if the last source I sent is correct, as I have:

23 FOR I = 1 TO 25: S = S + C(I): NEXT I

  for (int i=0; i<25; i++) {                                               // 23
    S = S + C[i];  
  }

32 FOR J = 2 TO 25

int initial=1;
for (int j=initial; j<25; j++) {                                         // 32 

In C++ an array of 5 elements have index: 0, 1, 2, 3, 4
so it is common to write the loop as:

for (i=0; i<5; i++)

instead of

for (i=0; i<=4; i++)

as if you have a dinamic allocated array, you should alwas check for his size, so

int size=5;

for (i=0; i<size; i++)

p.s.
If you start to code in a structured language (like C, C++, Pascal, Java), then you did not code any more in BASIC, due to the difficult that there is to write an easy to read source.
Else, programming in BASIC is more near to code as in Machine Language that in high level language, due to the use of GOTO (that it is the base instruction for flow control in Machine Language).

If you like interpretated language, then PHP, Python, Roby, Perl are structured language but more near to a free declaration of variables like in BASIC.

[Nataly-Mak]

ice00
спасибо за пояснения, теперь всё поняла с заданием переменной цикла.
Выбор языка - сложное для меня дело. Наверное, старею
Привычка сильная к Бейсику, на нём всё просто; программы я пишу очень быстро, отлаживаю за несколько минут. Вот только один минус - низкое быстродействие.
Мне все давно и настойчиво советуют перейти на другой язык, но я никак не соберусь. Во-первых, мало времени (потому что очень много всякой работы, и она у меня прибавляется, как снежный ком). Во-вторых, некому проконсультировать, а самой всё понять не всегда не удаётся. Вот и пользуюсь только Бейсиком. Но и тут есть свой плюс: пока у меня программа работает, я решаю какую-нибудь проблему на листе бумаге, думаю...

[BoBuk]

Nataly-Mak в сообщении #313788 писал(а):

Выбор языка - сложное для меня дело. Наверное, старею
Привычка сильная к Бейсику, на нём всё просто; программы я пишу очень быстро, отлаживаю за несколько минут. Вот только один минус - низкое быстродействие.
Мне все давно и настойчиво советуют перейти на другой язык, но я никак не соберусь. Во-первых, мало времени (потому что очень много всякой работы, и она у меня прибавляется, как снежный ком). Во-вторых, некому проконсультировать, а самой всё понять не всегда не удаётся. Вот и пользуюсь только Бейсиком. Но и тут есть свой плюс: пока у меня программа работает, я решаю какую-нибудь проблему на листе бумаге, думаю...

А что Вы никак не хотите освоить Delphi? В Вас столько энергии, вычислять все эти магические многогранники... Должно хватить энергии и на освоение языка, наиболее подходящего для таких целей.

[Nataly-Mak]

Так ведь языков-то очень много Все советуют разное: Паскаль, С, Delphi, PARI/GP и т. д. Я теряюсь... и продолжаю работать на Бейсике. Мне прислали компилируемый Бейсик, который работает гораздо быстрее интерпретируемого, которым я пользовалась раньше. А текст-то пишется совершенно одинаково!

Вот сейчас переписала-таки свою программу на C++, используя для этого текст предыдущей программы, который мне прислал ice00.
Ну, по образцу всё оказалось легко, тем более что программы эти очень похожи.
Ну, там "шапка" одна целый лист занимает, что в ней - бес её знает. Я её просто скопировала из старого текста.
А дальше всё просто уже.
Сейчас отошлю текст программы ice00, авось что-нибудь получится.

Не боги горшки обжигают! Это известная мудрость.

[BoBuk]

Nataly-Mak в сообщении #313825 писал(а):

Так ведь языков-то очень много Все советуют разное: Паскаль, С, Delphi, PARI/GP и т. д. Я теряюсь... и продолжаю работать на Бейсике. Мне прислали компилируемый Бейсик, который работает гораздо быстрее интерпретируемого, которым я пользовалась раньше. А текст-то пишется совершенно одинаково!

Так Вы даже не на VB пишете и даже не на компиляторе. Обалдеть...
Delphi - это паскаль и есть. Только позволяет писать приложения для Windows. Причём, очень быстро. Быстрый компилятор (традиционно). И быстрое исполнение, чуть уступающее C.
Так что рекомендую. Поможем, если что.

Цитата:

Вот сейчас переписала-таки свою программу на C++, используя для этого текст предыдущей программы, который мне прислал ice00.
Ну, по образцу всё оказалось легко, тем более что программы эти очень похожи.
Ну, там "шапка" одна целый лист занимает, что в ней - бес её знает. Я её просто скопировала из старого текста.
А дальше всё просто уже.
Сейчас отошлю текст программы ice00, авось что-нибудь получится.
Не боги горшки обжигают! Это известная мудрость.

Ну Вам же не драйвера писать, чтоб C++ использовать.

[Nataly-Mak]

Программа получилась супер! Работает очень быстро.
Если по предыдущей программе не было найдено за 4 часа ни одного классического пандиагонального квадрата, то по новой программе такой квадрат нашёлся практически мгновенно:

1 17 24 10 13
9 15 3 16 22
18 21 7 14 5
12 4 20 23 6
25 8 11 2 19

Однако с пандиагональными квадратами из простых чисел пока результатов нет. Из последовательных простых проверила уже 100 потенциальных массивов, пандиагонального квадрата не нашла.
Из произвольных простых проверила оба варианта наименьшего квадрата (с константой 233), тоже пандиагонального квадрата нет.

Может быть, совсем не случайно известен пандиагональный квадрат 6-го порядка из последовательных простых и неизвестны такие квадраты порядков 4 - 5. Вполне возможно, что автор квадрата 6-го порядка пытался построить и квадраты порядков 4 - 5. Не получилось?

Теперь осталось убедиться, что найденный мной ранее пандиагональный квадрат 5-го порядка из произвольных простых (с магической константой 853) является наименьшим. Задача непростая. Пока не вижу короткого пути её решения.

[Nataly-Mak]

Написала статью "Пандиагональные квадраты из простых чисел", в которой подробно изложила проблему построения таких квадратов.

[Nataly-Mak]

Итак, пандиагональные квадраты порядков 4-5 из последовательных простых чисел мне построить пока не удалось. Задача открыта.
Не удалось построить и пандиагональный квадрат 5-го порядка из произвольных простых чисел с магической константой меньше 853. Задача тоже открыта.

А я перехожу к построению пандиагонального квадрата 7-го порядка из простых чисел (последовательных или произвольных). Пандиагональный квадрат 6-го порядка из последовательных простых известен (он был здесь выложен; в OEIS этот квадрат в последовательности A073523).

maxal
у вас есть формула для пандиагональных квадратов 7-го порядка?

-- Вс май 02, 2010 15:04:27 --

В своей статье нашла пандиагональный квадрат 7-го порядка из чисел Смита:

567274     3279802  5859274     20502022   33961666  75835678  191489962
75839458 191484922  562234     3274762     5863054     20505802  33965446
20500762   33960406   75843238   191488702 566014    3278542     5858014
3282322      5861794    20504542    33964186   75838198  191483662 560974
191487442  564754     3277282    5856754   20499502   33967966  75841978
33962926   75836938   191482402 568534     3281062  5860534    20503282
5855494    20507062    33966706  75840718  191486182  563494    3276022

Можно использовать для тестирования программы (у меня пока нет такой программы, только собираюсь её создать).

Этот квадрат построен из чисел 7 арифметических прогрессий с одинаковой разностью (прогрессии были выложены здесь).
А вот из простых чисел я не нашла 7 арифметических прогрессий с одинаковой разностью
Поэтому аналогичный пандиагональный квадрат 7-го порядка из простых чисел не построила.

Задача: построить наименьший пандиагональный квадрат 7-го порядка из простых чисел (из последовательных или из произвольных, или из тех и других).
Ну, и из смитов можно попробовать, тем более что один уже имеется.

[maxal]

Nataly-Mak в сообщении #314911 писал(а):

у вас есть формула для пандиагональных квадратов 7-го порядка?

Абы какую формулу вывести легко. А вот эффективную с точки зрения вычислений пока не выводил.

[Nataly-Mak]

Ну, у меня пока и абы какой нет. Вот первая попытка сделать хоть какую:

пробую описать пандиагональный квадрат 7-го порядка системой линейных уравнений.
Пусть пандиагональный квадрат имеет следующий вид:

a1 x1 a2 x2 a3 x3 a4
x4 a5 x5 a6 x6 a7 x7
a8 x8 a9 x9 a10 x10 a11
x11 a12 x12 a13 x13 a14 x14
a15 x15 a16 x16 a17 x17 a18
x18 a19 x19 a20 x20 a21 x21
x22 x23 x24 x25 x26 x27 x28

Здесь смотрим на ai (i = 1, 2, 3, …, 21) как на символьные константы; xj (j = 1, 2, 3, …, 28) – переменные.
Теперь запишем условия магичности и пандиагональности этого квадрата:

a1+x1+a2+x2+a3+x3+a4=S
x4+a5+x5+a6+x6+a7+x7=S
a8+x8+a9+x9+a10+x10+a11=S
x11+a12+x12+a13+x13+a14+x14=S
a15+x15+a16+x16+a17+x17+a18=S
x18+a19+x19+a20+x20+a21+x21=S
x22+x23+x24+x25+x26+x27+x28=S
a1+x4+a8+x11+a15+x18+x22=S
x1+a5+x8+a12+x15+a19+x23=S
a2+x5+a9+x12+a16+x19+x24=S
x2+a6+x9+a13+x16+a20+x25=S
a3+x6+a10+x13+a17+x20+x26=S
x3+a7+x10+a14+x17+a21+x27=S
a4+x7+a11+x14+a18+x21+x28=S
a1+a5+a9+a13+a17+a21+x28=S
a4+a7+a10+a13+a16+a19+x22=S
a1+x7+x10+x13+x16+x19+x23=S
x1+x4+a11+a14+a17+a20+x24=S
a2+a5+a8+x14+x17+x20+x25=S
x2+x5+x8+x11+a18+a21+x26=S
a3+a6+a9+a12+a15+x21+x27=S
x3+x6+x9+x12+x15+x18+x28=S
a4+x4+x8+x12+x16+x20+x27=S
x3+x7+a8+a12+a16+a20+x26=S
a3+a7+a11+x11+x15+x19+x25=S
x2+x6+x10+x14+a15+a19+x24=S
a2+a6+a10+a14+a18+x18+x23=S
x1+x5+x9+x13+x17+x21+x22=S

S тоже символьная константа (магическая константа квадрата).
Имеем систему из 28 линейных уравнений с 28 неизвестными.
К сожалению, у меня нет ни одного пакета математических программ.
Можно ли решить данную систему уравнений?

Может быть, не совсем удачно составила систему. Это первая попытка.

Если кто-то может решать системы в каком-нибудь пакете программ (например, Maple), попробуйте, пожалуйста.
Интересно, какое получится решение.

[maxal]

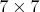
Вот "абы какая" формула для пандиагонального квадрата $7\times 7$, зависящая от 24 переменных и магической суммы.
Элементы квадрата (занумерованные в естественном порядке) соответсвуют строкам в нижеприведенной матрице (а каждый столбец - одной переменной, последний - магической сумме). Например, первая строка трактуется так: первый элемент квадрата равен сумме 1-й, 5-й, 10-й, 16-й и 23-й переменной.

[1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0]
[-1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0]
[0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, -1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0, 0, 0, -1, 0, 0, 0, -1, 0, 0, 0, -1, 0, 0, -1, 0, -1, 0, 0, 0]
[0, 0, 1, -1, 0, 0, 0, 0, 0, 0, -1, 0, 0, -1, 0, -1, 0, -1, 0, 0, -1, 0, 0, 0, 0]
[0, 0, -1, 0, 0, -1, 0, 0, 0, -1, 0, 0, 1, 0, -1, 0, 0, 0, 0, 0, 0, 0, -1, -1, 1]
[0, 0, 0, 0, -1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0]
[0, -1, 0, 0, 0, -1, 1, 0, -1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, -1, 0, -1, 1, 0, -1, -1, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, -1, -1, 0]
[1, 0, 0, -1, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 1, 0, 0, 0, 1, 0, 0]
[0, 1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
[-1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, -1, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 1, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0]
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 1]
[-1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, -1, 0, 0]
[0, -1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[1, 0, -1, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, -1, 0, 0, 0, -1, 0]
[-1, 0, 0, 0, -1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, -1, 0, 0]
[1, -1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, -1, 1, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0]
[0, 1, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0]
[0, 0, 0, -1, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0]
[0, 0, -1, 1, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
[0, 0, 1, 0, 0, 1, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 1, -1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, -1, 0, 0, 0, 1]
[0, 0, 0, 0, 0, 0, -1, 0, 0, -1, 0, -1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 1, -1, -1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, -1, -1, 0, 0, 0, 0, -1, 0, -1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, 1]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, -1, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, 0, 0, -1, -1, -1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, -1, -1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, -1, -1, -1, -1, -1, 1]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]

[Nataly-Mak]

Я составила по вашей формуле такой пандиагональный квадрат 7-го порядка:

55 56 25 -77 -81 232 90
2 -88 13 328 57 31 -43
66 274 -30 46 -6 18 -68
39 11 -39 33 3 -14 267
31 44 -3 -66 289 -7 12
-64 -16 314 15 16 17 18
171 19 20 21 22 23 24

Вы получили эту формулы, описав пандиагональный квадрат системой линейных уравнений?

Пока не вижу, как можно приспособить вашу формулу к построению пандиагонального квадрата 7-го порядка из простых чисел.

Представленную мной систему уравнений никто не желает помочь решить. Очень интересно, какое решение даст эта система.