1. Читаем старт-топик и смотрим на формулу:

Это формула, когда линия (

справа от =) уже появилась. Тогда слева "1" - точка,

- расстояние между соседними точками, а
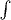
- градиент открытого типа. Еще не задано направление (в частном случае - пределы интегрирования) и угол интегрирования (частный случай - множитель

) при

.
-- Чт авг 26, 2010 23:00:33 --Эта единица уже сыграла злую шутку над человечеством. Эта шутка выглядит так:

. Я понимаю, конечно, чертишь график

, смотришь на интегральную площадь и, попробуй объясни, что означает выражение

. Тем более, когда общепризнано выражение

. Чем-то напоминает басню о мартышке и очках. У меня даже созрела такая аналогия: смотрят дикари на то, как капает вода из крана и, рассуждая, придумывают науку о том, как эти капельки внутри крана располагаются и по какому закону оттуда выкатываются. Точно, как физики с электроном...



