P. S. Единственное, что с ходу вызывает сомнение: верно ли, что для различных ординалов


Попробую вспомнить, как оно всё.
Множество называется транзитивным, если каждый его элемент является его подмножеством. Ординалом называется транзитивное множество с транзитивными элементами.
Ниже до конца поста рассуждаем исключительно в ZF, не используя аксиому выбора.
Утв. 0: Элементы ординалов --- ординалы.
Доказательство. Пусть

--- ординал и

. Тогда

транзитивно. Если

, то

и

транзитивно, так что элементы

тоже транзитивны.
Утв. 1: Для любых двух ординалов

,

либо

, либо
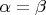
, либо

.
Доказательство. Скажем, что два ординала сравнимы, если для них выполняется данное утверждение.
Пусть

--- ординал, не сравнимый с каким-то ординалом

. Если

содержит элементы, не сравнимые с каким-то ординалом, то можно взять

, состоящее из таких элементов и в

по аксиоме регулярности выбрать элемент, не содержащий элементов

, после чего рассмотреть этот элемент в качестве

. Таким образом, можно считать, что любой элемент

сравним с любым ординалом. Если для какого-то

выполнено

или

, то

, чего не может быть. Значит,

. В силу

и аксиомы регулярности существует

, такой что

. По выбору

имеем

. Пусть

. Если

или

, то

, чего не может быть. Значит,

. Таким образом,

,

и

. Противоречие.
Утв. 2: Если

--- ординал, то

--- вполне упорядоченное множество.
Доказательство. Предыдущее утверждение + определение ординала + аксиома регулярности.
Утв. 3: Если

и

--- различные ординалы, то

.
Доказательство. По утверждению 1 один из наших ординалов является элементом другого. Пусть, для определённости,

. Пусть

--- изоморфизм ВУМов. Пусть

--- Наименьший ординал, такой что

. Получаем очевидное противоречие...
Вроде всё в порядке, аксиому выбора нигде не использовал
 -- Пн апр 19, 2010 06:00:21 --
-- Пн апр 19, 2010 06:00:21 --Ха, так это что получается?! Если аксиома выбора не верна, то существует ординал, не сравнимый по мощности с каким-то множеством.
А чему может быть равен наименьший такой ординал. У меня есть подозрение, что можно предложить модель ZF, в которой наименьший такой ординал будет равен

. Надо подумать...
-- Пн апр 19, 2010 06:07:27 --Но если этот ординал счётен, то должно существовать бесконечное множество, которое меняет мощность при добавлении одного элемента. Чудно...
-- Пн апр 19, 2010 06:09:54 --А, ну да. Это как раз и будет множество, бесконечное в смысле "неравномощно натуральному числу", но не бесконечное в смысле "равномощно собственному подмножеству". Вроде при отрицании аксиомы выбора такие штуки могут вылазить.



