Квант гравитации

[Someone]

Катющик писал(а):

Под экранированием не имелось ввиду поглощение в энергетическом смысле.
Под экранированием имелось ввиду геометрическое ограничение воздействия от комплекса удаленных объектов.

В этом вопросе Вы не смогли отследить мою логику в силу того, что накопились разногласия из верхних постов:
- например кажущаяся недоказанность равномерности распределения вещества..
Очень хочется с Вами поговорить, нужна ясность в формате беседы.

Начхать на недоказанность равномерности и прочее. Точно сформулируйте свои исходные посылки и предъявите расчёт взаимодействия. В таком стиле, как это сделал я: мало слов, много вычислений. Если будете продолжать болтовню, никто к Вам серьёзно относиться не будет.

Также учтите, что я и имел в виду "геометрическое ограничение воздействия", как полное ($\alpha=1$), так и частичное ($0<\alpha<1$). При $\alpha=0$ никакого экранирования вообще нет. Если Вам не нравится использованная мной модель, точно сформулируйте свою и предъявите расчёт.

Катющик писал(а):

По Вашему сценарию мне надлежит в открытом режиме выложить буквально все . Вплоть до квантового гравитационного сценария, теории поля,схемы волнообразования, а так же выложить (пусть это прозвучит смешновато ) «теорию массы».

Другие учёные именно так и поступают: публикуют результаты своих исследований для всеобщего сведения.

Но никого не интересует вся Ваша теория, пока нет внятного доказательства того, что она даёт правильное взаимодействие физических тел. Мои расчёты приводят к выводу, что у Вас правильного взаимодействия не получается. Поскольку мои расчёты опубликованы, и каждый может их проверить, Вашим заверениям, что у Вас всё правильно получается, никто не поверит, пока Вы не продемонстрируете свои вычисления.

[Лама]

Катющик писал(а):

Про ссылку от Ламы:
Ссылка верная.
А трактуя результаты Лама – искажает информацию. Проще говоря врет.
Убедиться можно пройдя по ранее указанной ссылке.
Если Вы уважаемый Лама со мной не согласны то пожалуйста коротко и ясно выразите мысль по существу .
Например:
Версия отталкивания – невозможна по …такой то причине.
А я (в случае если Вы сморозите чушь) – натыкаю вас носом.

Вам уже столько раз выражали возражения по существу, и столько раз тыкали носом как в намороженную Вами чушь, так и в отсутствие от Вас ответов на конкретные вопросы и обнаруженные у вас противоречия в самых основаниях вашей "теории", что делать это еще раз нет никакого смысла. Поэтому я и написал, что никаких аргументов Вы не воспринимаете. Можете считать, что я искажаю информацию. Каждый может составить собственное мнение о ее ложности или правдивости, пройдя по ссылке. Но с форума физфака Вы таки смылись, прервав свое участие в дискуссии. Может, оттого, что считаете там всех умными, а я и в этом Вас оболгал?

[Катющик]

Лама ,
выразите мысль по существу .
Например:
Версия отталкивания – невозможна по …такой то причине.
Форум физфака МГУ по уровню детства – лидер.
Хотя в форуме и есть способные оперативно мыслить (например Owen)


Для тех кто читает тему:
Крутой мехматовский форумчанин Someone практически признал что на силах притяжения Вселенная разлетаться не может, поскольку уже признал что:
силами притяжения нельзя заставить барионные частицы разлетаться.
ознакомиться можно здесь:
http://www.relativity.ru/forum/viewtopic.php?t=2413&start=240&sid=62fb4526acfc5ced0e35c06358494653

[Someone]

Катющик писал(а):

Крутой мехматовский форумчанин Someone практически признал что на силах притяжения Вселенная разлетаться не может, поскольку уже признал что:
силами притяжения нельзя заставить барионные частицы разлетаться.
ознакомиться можно здесь:
http://www.relativity.ru/forum/viewtopic.php?t=2413&start=240&sid=62fb4526acfc5ced0e35c06358494653

Вы забыли упомянуть: при нулевых начальных скоростях. Это условие Вы сами поставили. Правда, я не знаю, как Вы хотите эти условия осуществить.

Ну, а если фразу

Someone писал(а):

А вселенная разлетается, и, как ни кажется Вам нелепым, МОЖЕТ разлетаться, даже если никакого отталкивания нет.

считать признанием того, что Вселенная разлетаться НЕ может, тогда, конечно, "практически признал".

Так как, Катющик-Viictor, если между двумя частицами в Вашей схеме находится третья, отталкивание между ними ослабляется или нет? Это практически самый главный вопрос, на который Вы должны ответить. Уже который раз спрашиваю. ДА или НЕТ?

[Аурелиано Буэндиа]

Катющик писал(а):

Для тех кто читает тему:

У меня, да и не только у меня, создалось впечатление, что Ваша единственная цель — развести малонаучную демагогию и уболтать собеседников (так сказать закидать шапками).

Катющик писал(а):

...Я знаю не менее пяти исследователей только в Москве, которые говорят примерно это же. И у каждого свой неповторяемый взгляд на мироздание и процессы в нём, своя непререкаемая аргументация.

Как быть?

Как быть?
1) Прекратить лгать о "непререкаемой аргументации" и разводить пустую болтавню, а также
2) ответить на поставленные Вам вопросы.
До тех пор пока Вы не опровергли аргументы против Вашей "теории" рассуждения о "непререкаемости" являются ложью.

[Катющик]

Другие частицы (барионные, введенные в расчет) не могут влиять на уменьшение результирующей силы, они её могут только наращивать, поскольку вносят дополнительную силовую составляющую той же природы..
Что здесь можно спрашивать?

Цитата:

при нулевых начальных скоростях. Это условие Вы сами поставили.

Это общий базовый случай, все отклонеия по скорости задаются именно от этой базовой схемы.
Вы не сможете ни до чего исхитриться изменяя начальную скорость , поскольку на какое удаление бы Вы не вышли,
Вы получите сколь угодно малые , но в любом случае не равные нолю значения сил. Если Вы в дальнейшем перейдете от двух частиц к множеству частиц - общее значение силы будет нарастать.

Цитата:

считать признанием того, что Вселенная разлетаться НЕ может, тогда, конечно, "практически признал".

Достаточно Вашего:

Цитата:

силами притяжения нельзя заставить барионные частицы разлетаться

Остальное - жесткие следствия одного из другого.

[Катющик]

2 Аурелиано Буэндиа

Цитата:

У меня, да и не только у меня, создалось впечатление,

Впечатления, мнения - может пора уже от впечатлений к мыслям переходить?
Вы в этой теме как модератор или как собеседник?
Если хоть иногда как собеседник, то у нас с Вами остался неразрешенный вопрос по графикам.
Да и не только в этом , а и в любом вопросе чтобы разобраться мало одних впечатлений.

[Аурелиано Буэндиа]

Катющик писал(а):

Если хоть иногда как собеседник, то у нас с Вами остался неразрешенный вопрос по графикам.
Да и не только в этом , а и в любом вопросе чтобы разобраться мало одних впечатлений.

Ну конечно впечатлений мало. Ну а что же мне остается если Вы не отвечаете на критику и поставленные Вам вопросы?
И дело даже не в графиках.

1) Вы так и не смогли обосновать почему при притяжении невозможны устойчивые орбиты.
Я же привел аргументы почемы такие устойчивые орбиты возможны.
Июл 25, 2006 18:06:46
2) Вы не ответили ничего вразумительного на указание несостоятельности Вашей теории которое я Вам привел
Вт Июл 25, 2006 21:41:29
3) Вы не ответили на мой вопрос о радиусе частиц
Июл 26, 2006 16:26:57

С тех пор уже прошло полторы недели, а реакции ноль. Если Вы не можете ответить не отвечайте, только не надо делать пафосные заявления о "непогрешимости".

[Someone]

Катющик писал(а):

Другие частицы (барионные, введенные в расчет) не могут влиять на уменьшение результирующей силы, они её могут только наращивать, поскольку вносят дополнительную силовую составляющую той же природы..
Что здесь можно спрашивать?

Таким образом, положение следующее. Гравитационного притяжения нет, есть только гравитационное отталкивание. Берём две частицы. Они отталкиваются с некоторой силой. Вводим между ними третью. В результате отталкивание первых двух частиц усиливается. А откуда берётся экранирование? Для экранирования отталкивание должно ослабляться!

Но Вы, конечно, запутались в собственных построениях. Разумеется, введённая третья частица отталкивает две первые в противоположные стороны, причём, сильнее, чем они отталкивали друг друга, так как она ближе к каждой из них, а отталкивание у вас обратно пропорционально квадрату расстояния. Но нас отталкивание, создаваемое третьей частицей, в данный момент не интересует. Вопрос был о силе отталкивания именно двух первых частиц. Экранирование означает, что при введении третьей частицы уменьшается именно отталкивание двух первых частиц, без учёта отталкивания, создаваемого третьей частицей.

Катющик писал(а):

Цитата:

при нулевых начальных скоростях. Это условие Вы сами поставили.

Это общий базовый случай, все отклонеия по скорости задаются именно от этой базовой схемы.
Вы не сможете ни до чего исхитриться изменяя начальную скорость , поскольку на какое удаление бы Вы не вышли,
Вы получите сколь угодно малые , но в любом случае не равные нолю значения сил. Если Вы в дальнейшем перейдете от двух частиц к множеству частиц - общее значение силы будет нарастать.

Я же Вам неоднократно говорил: читайте учебник механики. Там всё объясняется. Но Вы просто потрясающе невежественны. Вы хотя бы слышали такие слова, как "первая космическая скорость", "вторая космическая скорость"? Я в семилетнем возрасте знал, что они означают. Может быть, время было такое? Только что запустили первый искусственный спутник Земли. Чтобы он не упал на Землю, ему нужно было сообщить первую космическую скорость - примерно 8 км/сек. А чтобы он совсем улетел от Земли, ему нужно сообщить вторую космическую скорость - примерно 11,2 км/сек. Понимаете: улетел совсем и никогда не вернулся. Несмотря на то, что между ним и Землёй есть только сила притяжения, и на любом расстоянии это притяжение не исчезает. Ну, в реальной Солнечной системе в дело вмешивается Солнце, которое меняет картину движения космического аппарата, когда он достаточно удалится от Земли, но мы ведь не об этом говорим. Чтобы насовсем улететь и от Солнца, просто скорость нужна немного побольше.

Так что я просто не понимаю, почему я должен доказывать Вам расчётами то, что можно прочесть в учебнике и что, по моим представлениям, должен бы знать любой мало-мальски образованный человек. Вы же в школе астрономию изучали? Там наверняка об этом говорилось. Ну ладно уж, я проделаю для Вас это упражнение. Поймёте ли Вы - не знаю, но это Ваша проблема.

Катющик писал(а):

Достаточно Вашего:

Цитата:

силами притяжения нельзя заставить барионные частицы разлетаться

Остальное - жесткие следствия одного из другого.

Ещё раз повторяю: речь идёт о случае, когда частицы имеют начальные скорости, равные нулю. В таких условиях сила притяжения неизбежно заставит частицы упасть друг на друга. Однако при ненулевых скоростях ситуация может оказаться совершенно другой. Результат зависит от положения частиц, величин и направлений их скоростей.

Рассмотрим две одинаковые частицы с массами $m_0$. Систему координат выберем так: начало системы координат совпадает с центром масс системы частиц, то есть, в данном случае, находится точно посередине между ними, а ось $Ox$ проходит через наши частицы. Пусть та частица, которая находится на положительной части оси, в момент времени $t$ имеет координату $x(t)>0$, тогда другая будет иметь координату $-x(t)$. Дальше я вместо $x(t)$ буду писать просто $x$. Я буду рассматривать только простейший случай, когда частицы движутся вдоль оси $Ox$. Общий случай Вам всё-таки придётся посмотреть в учебнике, иначе мне придётся убить целый день, а то и больше, набирая формулы и объяснения к ним.

Уравнение движения получается из второго закона Ньютона: ускорение частицы равно действующей на неё силе, делённой на массу частицы. Ускорение есть вторая производная координаты частицы по времени, то есть, $\ddot x$, расстояние между частицами равно $2x$, а сила, действующая на частицу с координатой $x$, равна $-\frac{km_0^2}{(2x)^2}=-\frac{km_0^2}{4x^2}$. Знак "минус" поставлен потому, что сила, приложенная в к частице с положительной координатой, направлена в отрицательном направлении, а $k$ - гравитационная постоянная. Подставляя во второй закон Ньютона, получим уравнение $\ddot x=-\frac{km_0}{4x^2}$. Мне не хочется всё время писать такую кучу букв, поэтому я буду считать, что единицы измерения физических величин у нас выбраны так, что $\frac{km_0}4=1$, тогда уравнение будет выглядеть попроще: $\ddot x=-\frac 1{x^2}$. Осталось решить это уравнение. Оно имеет бесконечное множество решений, описывающих всевозможные варианты движения двух частиц вдоль оси $Ox$. Я не буду находить их все, потому что это громоздко, найду только одно, в котором частицы бесконечно разлетаются и никогда не возвращаются.

Для начала умножим обе части нашего уравнения на соответствующие части тождества $2\dot xdt=2dx$. Получится $2\dot x\ddot xdt=-\frac{2dx}{x^2}$. Заметим, что $2\dot x\ddot xdt=2\dot xd\dot x=d(\dot x^2)$, а в правой части $-\frac{2dx}{x^2}=2d\left(\frac 1x\right)$, так что уравнение принимает вид $d(\dot x^2)=2d\left(\frac 1x\right)$.

Вычисляя интегралы от обеих частей полученного уравнения, получим $\dot x^2=\frac 2x+C_1$, где $C_1$ - какое угодно число. При $C_1<0$ получаются решения, в которых частицы сначала разлетаются, а потом падают друг на друга, а при $C_1\geqslant 0$ - решения, в которых частицы бесконечно разлетаются. Простейший вариант получается при $C_1=0$, но я возьму более сложный вариант: $C_1=2$. Тогда получится уравнение $\dot x^2=2\left(\frac 1x+1\right)$, то есть, $\dot x=\pm\sqrt{\frac{2(1+x)}x}$.

Производная $\dot x$ есть скорость частицы; так как частицы разлетаются, то скорость частицы с координатой $x$ направлена в сторону увеличения $x$, то есть, $\dot x\geqslant 0$, поэтому в нашем уравнении нужно взять знак $+$; получаем $\dot x=\sqrt{\frac{2(1+x)}x}$.

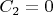
Умножая на $dt$ ($\dot xdt=dx$) и деля на $\sqrt{\frac{1+x}x}$, получаем уравнение $\sqrt{\frac x{1+x}}dx=\sqrt{2}dt$. Осталось вычислить интегралы от обеих частей и получить $\sqrt{x(1+x)}+\ln(\sqrt{1+x}-\sqrt{x})=\sqrt{2}t+C_2$, где $C_2$ - ещё одно произвольное число, которое в данном случае определяет начало отсчёта времени. Я возьму просто $C_2=0$, и после деления на $\sqrt{2}$ получится искомое решение в виде

$$t=\sqrt{\frac{x(1+x)}2}+\frac 1{\sqrt{2}}\ln(\sqrt{1+x}-\sqrt{x})$$

.

Здесь решение получилось не в виде зависимости координаты частицы от времени, а в виде обратной зависимости: мы задаём любую координату $x>0$, и, подставив в эту формулу, находим момент времени $t$, когда частица будет иметь такую координату, а по формуле $v=\dot x=\sqrt{\frac{2(1+x)}x}=\sqrt{2\left(\frac 1x+1\right)}$ можем найти скорость частицы в этот момент. Из последнего выражения легко увидеть, что, по мере увеличения $x$, скорость частицы постепенно уменьшается, но всегда остаётся больше $\sqrt{2}$, так что частица никогда не остановится и не повернёт назад.

Ну, вот Вам и бесконечный разлёт частиц, на которые действует только сила притяжения.

Вообще, я потратил на эту глупую писанину уйму времени, которое я мог бы потратить более полезным способом, если бы Вы снизошли до чтения учебника.

[Катющик]

Цитата:

При получаются решения, в которых частицы сначала разлетаются, а потом падают друг на друга, а при - решения, в которых частицы бесконечно разлетаются.

Считали считали и досчитались .
Своим расчетом Вы как минимум отменили Второй закон Ньютона который гласит - скорость изменения импульса тела равна векторной сумме действующих на него сил:
Строим график действующих на тело сил.
Он выглядит как $1/R^2$,
На графике четко видно что с увеличивая значении R мы получим сколь угодно малые , но не равные нолю значения.
Мы не получим F=0
А поскольку мы не получим F=0, то векторная сумма действующих на него сил тоже не будет равна нолю.
Кроме того не трудно заметить что векторная сумма действующих на тело(на барионную частицу) сил зависит не от времени а от расстояния.
В заданной Вами схеме с начальной скоростью (при любых значениях скорости ) тело ни когда не достигнет предела R (или 2R) при котором на него будет действовать F=0.
А значит на тело всегда будет действовать сколь угодно малая , но в любом случае не равная нолю сила,
Из чего однозначно (согласно второго Закона Ньютона(ознакомиться можно например здесь: http://www.karelia.ru/psu/Chairs/KOF/mathemat/lectures/lecture5_a.html )
однозначно следует что будет иметь место скорость изменения импульса, как следствие изменение скорости барионной частицы.
В Вашем расчете это банально упразднено .
Пару слов о скорости:
Мы не можем брать фантастические значения скорости.
начальная скорость как минимум не может быть больше скорости света.
Кроме того скорость барионной частицы не может даже сопоставимо приближаться к скорости света. (подобной практики отмечено(зафиксировано) в наблюдаемой картине не было)

Цитата:

Для экранирования отталкивание должно ослабляться!

Вам уже неоднократно объяснили что речь ведется об экранировании воздействия от комплекса причем о геометрическом экранированиии а не о силовом.
Скажите какого объема информации Вам достаточно?.
Предположим , что я предоставлю вам схему экранирования. Вы убедитесь что она верна.
Дальше что?

[Лама]

Катющик писал(а):

Лама ,
выразите мысль по существу .
Например:
Версия отталкивания – невозможна по …такой то причине.
Форум физфака МГУ по уровню детства – лидер.
Хотя в форуме и есть способные оперативно мыслить (например Owen)

По существу: возможна любая версия, которая только может взбрести Вам в голову. Но все они останутся лишь Вашими домыслами до тех пор, пока Вы не ДОКАЖЕТЕ РАСЧЕТАМИ их соответствие ЧИСЛЕННЫМ ЗНАЧЕНИЯМ всех известных фактов, относящихся к теме версии. А у Вас даже на качественном уровне концы с концами не сходятся, как Вам показывают люди, умеющие оперативно мыслить. Проблема лишь в том, что это именно Вы, похоже, задержались в детстве, а взрослые дяди возятся с Вами, как с капризным дитятей. Вы, например, даже не поняли того, что Вам только что сказали о центробежной силе (я думаю, Вы не поняли даже того, что Вам сказали именно о ней), равно как не понимаете, что даже наличие отрицательного ускорения не обязательно приведет к обращению скорости в 0 на конечном расстоянии от источника силы.
Впрочем, возможно, я ошибаюсь, и в оценке Ваших действий более прав А.Б.

[Катющик]

Лама ,
выразите мысль по существу .
Например:
Версия отталкивания – невозможна по …такой то причине.
А если Вы не всостоянии выражать мысли по существу - возвращайтесь в детский форум физфака МГУ,

Цитата:

что даже наличие отрицательного ускорения не обязательно приведет к обращению скорости в 0 на конечном расстоянии от источника силы.

и там подумайте для какого линейного отрезка и для какого промежутка времени это действительно.

[Someone]

Катющик писал(а):

Считали считали и досчитались .
Своим расчетом Вы как минимум отменили Второй закон Ньютона который гласит - скорость изменения импульса тела равна векторной сумме действующих на него сил:

Зачем так нагло врать, причём, людям, которые понимают, что Вы врёте? Или Вы просто вообще ничего не понимаете? Попробую разжевать дальше, но надежда на то, что Вы поймёте, близка к нулю. Откуда я, по Вашему мнению, взял уравнение $\ddot x=-\frac 1{x^2}$? Я же чётко сказал: из второго закона Ньютона: $a=\frac F{m_0}$, где $a$ - ускорение; если хотите, перепишу его в виде $\frac{d(m_0v)}{dt}=F$, где $v$ - скорость частицы, $m_0v$ - её импульс, а $\frac{d(m_0v)}{dt}$ - "скорость" изменения импульса. При движении по оси $Ox$ (а мы рассматриваем именно этот случай) скорость есть производная от координаты по времени: $v=\frac{dx}{dt}=\dot x$ (здесь не надо думать, почему $\frac{dx}{dt}=\dot x$, это просто два разных обозначения производной; второе обычно используется вместо первого для упрощения записи формул). Дальше: $\frac{d(m_0v)}{dt}=m_0\frac{dv}{dt}=m_0\frac{d^2x}{dt^2}=m_0\ddot x$; постоянный множитель $m_0$ за знак производной выносится, а $\frac{d^2x}{dt^2}=\ddot x$ - два разных обозначения второй производной. Сила гравитационного притяжения по Ньютону равна $F=-\frac{km_0^2}{R^2}=-\frac{km_0^2}{4x^2}$, поскольку при нашем выборе системы координат расстояние между частицами $R=2x$ (нарисуйте себе простенькую картинку: ось $Ox$, точка $O$ - начало системы координат, в точке оси с координатой $x>0$ - одна частица, симметрично ей относительно начала координат в точке с координатой $-x$ - другая частица; прошлый раз я объяснял, почему так; сила притяжения, действующая на первую частицу со стороны второй, направлена в отрицательную сторону, поэтому в формуле стоит знак "$-$"). Теперь подставляем все выражения в запись второго закона Ньютона и получаем $m_0\ddot x=-\frac{km_0^2}{4x^2}$, а после сокращения на $m_0$ - в точности то уравнение, которое я писал прошлый раз. Ну, а выбор единиц измерения - дело хозяйское. Если хотите, всё то же самое можно переписать в системе Си или любой другой.

Катющик писал(а):

Строим график действующих на тело сил.
Он выглядит как $1/R^2$,
На графике четко видно что с увеличивая значении R мы получим сколь угодно малые , но не равные нолю значения.
Мы не получим F=0

Совершенно верно, не получим. А где у меня $F=0$? Врать-то не надо. Покажите точно, где у меня $F=0$.

Катющик писал(а):

А поскольку мы не получим F=0, то векторная сумма действующих на него сил тоже не будет равна нолю.

Далась Вам эта векторная сумма. У нас всего одна сила, действующая вдоль оси $Ox$. Поэтому она определяется одним числом.

Катющик писал(а):

Кроме того не трудно заметить что векторная сумма действующих на тело(на барионную частицу) сил зависит не от времени а от расстояния.

Опять враньё. Покажите, где у меня написана зависимость от времени, а не от расстояния.

Катющик писал(а):

В заданной Вами схеме с начальной скоростью (при любых значениях скорости ) тело ни когда не достигнет предела R (или 2R) при котором на него будет действовать F=0.
А значит на тело всегда будет действовать сколь угодно малая , но в любом случае не равная нолю сила,
Из чего однозначно (согласно второго Закона Ньютона(ознакомиться можно например здесь: http://www.karelia.ru/psu/Chairs/KOF/mathemat/lectures/lecture5_a.html )
однозначно следует что будет иметь место скорость изменения импульса, как следствие изменение скорости барионной частицы.
В Вашем расчете это банально упразднено .

Опять врёте. Более того, я прямо написал, что скорость по мере разлёта частиц всё время уменьшается, и написал точную формулу: $v=\sqrt{2\left(\frac 1x+1\right)}$. Из неё хорошо видно, что чем дальше частицы разлетаются, то есть, чем больше $x$, тем меньше скорость. Только она всегда остаётся (в данном случае) больше $\sqrt{2}$, так что частицы нигде не останавливаются и продолжают разлетаться.

Катющик писал(а):

Пару слов о скорости:
Мы не можем брать фантастические значения скорости.
начальная скорость как минимум не может быть больше скорости света.

Не понял. Откуда вдруг выскочила скорость света? Вы же не знаете, какие у меня единицы измерения, может быть $\sqrt{2}$ в моих единицах - это 1 мм в год. Или 1 км в секунду. Подбирая единицы измерения, легко получить любую величину. Кроме того, Вы же работаете в рамках ньютоновских представлений, здесь никаких ограничений на скорость нет.

Катющик писал(а):

Кроме того скорость барионной частицы не может даже сопоставимо приближаться к скорости света. (подобной практики отмечено(зафиксировано) в наблюдаемой картине не было)

О Вашем невежестве можно рассказывать анекдоты. Вы что-нибудь про ускорители слышали? А термин "космические лучи" Вы встречали? Претенденту на создание всеобъемлющей картины мироздания такие вещи знать обязательно. Впрочем, когда Вы продемонстрировали незнание термина "вторая космическая скорость", само существование которого опровергает Ваши утверждения, особо удивляться уже нечему.

Катющик писал(а):

Цитата:

Для экранирования отталкивание должно ослабляться!

Вам уже неоднократно объяснили что речь ведется об экранировании воздействия от комплекса причем о геометрическом экранированиии а не о силовом.

Ваш "комплекс" состоит из тех же частиц, которые мы наблюдаем вокруг себя, или из каких-то других? Природа сил отталкивания, создаваемого частицами комплекса, та же самая, что для окружающих нас частиц, или другая? Что Вы понимаете под геометрическим экранированием и чем оно отличается от силового? Если между двумя частицами что-нибудь находится, что происходит с силой отталкивания между ними?

Ответьте, пожалуйста, на эти вопросы.

Катющик писал(а):

Скажите какого объема информации Вам достаточно?.
Предположим , что я предоставлю вам схему экранирования. Вы убедитесь что она верна.
Дальше что?

А что, та схема, которую Вы уже опубликовали на http://man.khakassia.ru/rus/science/, является ложной? То есть, Вы умышленно врёте?

[Лама]

Someone, похоже, он не врёт, а действительно просто не понимает. Вообще ничего. И это безнадежно
Пы.Сы. А на физфаковском форуме уверяли, что здесь-то уж модерация такая, что подобные персонажи не проходят. Хотя, вот за этот офф-топ я, может, и получу еще один фф-тык

[Катющик]

Ух как сильно заколдовано
2 Someone

Цитата:

. Вы что-нибудь про ускорители слышали? А термин "космические лучи" Вы встречали?

Ну достали уже.
Какие ускорители. Какие лучи. мы о тяготении говорим . Было сказано:

Цитата:

в наблюдаемой картине не было

Ну приведите мне пример перемещения для реального тела состоящего из барионного вещества, со скоростью близкой хотя бы к С/2 (система отсчета привязана к среднему вектору перемещения масс).
А если не можете , то хоть задумайтесь почему тела не могут достичь этих скоростей.

Цитата:

При получаются решения, в которых частицы сначала разлетаются, а потом падают друг на друга, а при - решения, в которых частицы бесконечно разлетаются.

Скажите мне пожалуйста
Вы какими соображениями руководствуетесь осуществляя данный выбор ?.
Если надо чтобы тело улетело - берете одно ,
а если надо чтобы упало - берете другое?

Цитата:

Впрочем, когда Вы продемонстрировали незнание термина "вторая космическая скорость", само существование которого опровергает Ваши утверждения

Я подозреваю что у вас
физический вакуум, окруженный пространством имеющим плотность близкую к вселенской ни сколько не отличается по частным свойствам от физического вакуума окруженного ненасыщенным пространством.
У вас для обоих версий – один комплект частных физических параметров , один сценарий разлета тяготеющих частиц.
В системе Земля - ракета при отсутствии(устранении) внешних тел (при вселенской плотности стремящейся к нулю) ни чего физически не меняется? Задал вторую космическую и всё.
Я уже пытался спрашивать: как вы согласны трактовать Закон всемирного Тяготения в общем виде?

Цитата:

Ваш "комплекс" состоит из тех же частиц, которые мы наблюдаем вокруг себя, или из каких-то других?

да конечно из тех же .

Цитата:

Природа сил отталкивания, создаваемого частицами комплекса, та же самая, что для окружающих нас частиц, или другая?

Та же самая.

Цитата:

Если между двумя частицами что-нибудь находится, что происходит с силой отталкивания между ними?

Если масса то она участвует во взаимодействии.

Цитата:

Что Вы понимаете под геометрическим экранированием и чем оно отличается от силового?

Из условия гравитационного равновесия Вселенной следует, что суммарные гравитационные воздействия встречно направленные по мировой линии равны между собой.
Данное условие возможно только при условии того что с обоих сторон от расчетной точки на мировой линии в гравитационном взаимодействии участвует равное количество масс.
Распределяя на любом участке мировой линии дополнительные массы мы тем самым исключаем равное вновь размещенному количество масс на конечном удалении вдоль мировой линии.

Из чего следует что для каждой единичной массы (материальной точки) рассматриваемого тела массой m приближающееся тело массой М ограничивает общее количество, участвующих в частном гравитационном взаимодействии, масс комплекса удаленных объектов.
Данное ограничение происходит, по каждой из мировых линий проходящих через рассматриваемую материальную точку (точечную массу) и приближающееся тело массой М, по всему образованному в результате приближения телесному углу, на величину соответствующую распределению масс по отрезку мировой линии, принадлежащему приближающемуся телу массой М.
Таким образом любое тело приближающееся к рассматриваемой материальной точке своим приближением геометрически исключает из гравитационного воздействия на точку определённый материальный слой на комплексе удаленных объектов.

[/quote]