А пожалуйста.
Соединяем их в соответствии с приведенными Вами формулами. Все получается.
А вообще, моя идея была в том, чтобы в арифметике положительных рациональных чисел в качестве “основных” выбрать иной набор операций, по сравнению с тем набором, который обычно выбирается. И сделать это для того, чтобы вскрыть объективно имеющуюся в системе положительных рациональных чисел внутреннюю симметрию, усмотреть и исследовать которую было бы труднее при “традиционном” наборе основных операций.
Фрагментарно я уже пытался поднять эту “электротехническую” тему, но здесь хотелось бы развить ее более систематически.
Свободный Художник писал(а):
... естественно расширить систему

, заставив действовать на ее множестве-носителе

свободную полугруппу строк

,
где
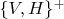
есть множество всех строк в алфавите
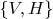
,

есть операция конкатенации строк (которую при записи термов будем, как правило, опускать).
Т. е. расширить систему

до системы

,
где

есть операция “действия”:
для любых чисел

, принадлежащих

и для любой строки

, принадлежащей
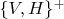
,
запись

означает, что число

является результатом действия строки

на число

.
Смысл операции

действия определяется смыслом определенных в предыдущих постах операторов

и

; например, если

и

, то

.
Далее вместо

будем также писать

.
Двойственность в системе

(или в системе

) естественно связать с двойственностью в электротехнике:
http://en.wikipedia.org/wiki/Duality_(electrical_circuits),
поскольку система

(или

) допускает естественную “электротехническую” интерпретацию.
Действительно, отметим прежде всего, что система

-- это “двухсортная” система, в которой имеются объекты двух сортов: строки символов в алфавите
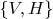
и числа из

(аналогично тому, как в векторных пространствах имеются объекты двух сортов: скаляры и векторы).
При электротехнической интерпретации мы интерпретируем строки символов в алфавите
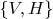
как “четырехполюники”, а числа из

-- как “двухполюсники” (число

из

интерпретируется как сопротивление соответствующего двухполюсника, в частности,

интерпретируется как двухполюсник короткого замыкания, а

-- как двухполюсник холостого хода).
Операция

интерпретируется как операция последовательного соединения двухполюсников,
операция

интерпретируется как операция параллельного соединения двухполюсников,
выражение

с фундаментальной для системы

операцией

“действия” интерпретируется как четырехполюсник

, нагруженный на сопротивление

;
в частности

обозначает четырехполюсник

в режиме короткого замыкания, а выражение

-- четырехполюсник

в режиме холостого хода.
-------------------------------
Оказывается, такого рода “алгебры двухполюсников и четырехполюсников” активно изучались:
Шестаков В. И. Алгебра двухполюсных схем, построенных исключительно из двухполюсников (алгебра А-схем)//Автоматика и телемеханика, 1941, № 2. — С. 15-24.
(об этой работе см.. в Бажанов В. А.
В.И. Шестаков и К. Шеннон. Разные судьбы творцов одной красивой идеи // Вопросы истории естествознания и техники, 2005, № 2. С. 112—121:
http://www.ulsu.ru/staff/homepages/bazhanov/russian/Viet_Shes05.pdf)
Телешев Юрий Владимирович
Алгебры пассивных двухполюсников:
http://ito.edu.ru/2000/II/3/391.html