Пространство Банаха

[Alexey1]

Здравствуйте!
Проверьте пожалуйста доказательство того, что пространство C[0,1] является полным. Просто я нашёл доказательство, но вот не совсем понимаю обоснованность первой его части.
Для доказательства необходимо показать, что любая последовательность Коши имеет предел в C[0,1].
Пусть ${x_n}$ является последовательностью Коши в C[0,1]. Для фиксированного $t\in[0,1], $ $|x_n(t)-x_m(t)| \leq ||x_n-x_m|| \rightarrow 0$. И таким образом, ${x_n}$ является последовательностью Коши в $R$. Так как $R$ является полным, то существует предел $x(t)$, такой что $x_n(t) \rightarrow x(t)$. Таким образом, функции $x_n$ сходятся поточечно к $x(t)$.
Теперь показываем, что сходимость является равномерной для $t \in [0,1]$.
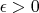
Для заданного $\epsilon >0$, выберем $N$ такое что $||x_n-x_m|| < \epsilon /2$ для $n,m>N$. Тогда для $n>N$
$|x_n(t)-x(t)| \leq |x_n(t) -x_m(t)|+|x_m(t)-x(t)| \leq ||x_n-x_m||+|x_m(t)-x(t)|$.
Затем, идёт фраза которую я не понимаю, а именно "Выбрав $m$ достаточно большим (которое может зависеть от $t$), каждое слагаемое в правой части неравенства меньше чем $\epsilon /2$ и таким образом, $|x_n(t)-x(t)|<\epsilon$".
По этой фразе возникает вопрос: Если можно в правой части сделать $|x_m(t)-x(t)|<\epsilon /2$, то тогда можно тоже самое сделать и для левой части. Но что тогда доказывать.

[RIP]

Alexey1 в сообщении #241088 писал(а):

По этой фразе возникает вопрос: Если можно в правой части сделать $|x_m(t)-x(t)|<\epsilon /2$, то тогда можно тоже самое сделать и для левой части.

Фишка в том, что $n$ (точнее, нижняя граница для $n$, т.е. $N$) не должно зависеть от точки $t$.

[Alexey1]

Спасибо за ответ. Однако, возьмём $t=t_1$, тогда находим $m_1=m(t_1)$, такое что $|x_{m_1}(t1)-x(t_1)|< \epsilon /2$. Таким образом, $|x_n(t_1)-x(t_1)|< \epsilon$. Но ведь это опять доказвает только поточечную сходимость. Что я не понимаю?

[RIP]

Alexey1 в сообщении #241094 писал(а):

Но ведь это опять доказвает только поточечную сходимость.

Неравенство $|x_n(t)-x(t)|<\epsilon$ будет выполняться для любого $t\in[0;1]$ (при любом $n>N$). Поскольку определение $N$ никак не зависит от $t$, то это означает, что сходимость равномерная (т.е. по метрике $C[0;1]$).
$m=m(t)$ участвует только в доказательстве этого неравенства, но не в формулировке.

[AGu]

Не забудьте еще заметить (или доказать), что возникшая функция $x:[0,1]\to\mathbb R$ непрерывна.

[ewert]

AGu в сообщении #241138 писал(а):

Не забудьте еще заметить (или доказать), что возникшая функция $x:[0,1]\to\mathbb R$ непрерывна.

Доказывать не надо: это -- предыдущая теорема.

[Alexey1]

А почему Вы считаете, что это предыдущая теорема? В том доказательстве, которое у меня есть, при доказательстве непрерывности используется именно этот, уже доказанный факт.

[ewert]

Alexey1 в сообщении #241229 писал(а):

А почему Вы считаете, что это предыдущая теорема? В том доказательстве, которое у меня есть, при доказательстве непрерывности используется именно этот, уже доказанный факт.

Парадокс. Вот ровно это и означает, что она -- предыдущая.

[Alexey1]

Встретил ещё одно доказательство, но оно очень сжатое. Как обосновывается следующее
$||f_n(x)-f_m(x)||<\epsilon , n,m>N \Longrightarrow ||f(x)-f_m(x)||\leq \epsilon , m>n, x\in[0,1]$.
$\lim f_n(x)=f(x)$ только для фиксированного $x$, а в приведённом выражении получается, что предел выполняется для всех $x\in[0,1]$.
Разве $\lim f_n(x)=f(x)$ поточечно $\Longrightarrow$ $\lim f_n(x)=f(x), x\in[0,1]$?

[RIP]

Alexey1 в сообщении #241280 писал(а):

Разве $\lim f_n(x)=f(x)$ поточечно $\Longrightarrow$ $\lim f_n(x)=f(x), x\in[0,1]$?

Не знаю, что Вы понимаете под второй записью (или под первой...), но, вообще-то, это одно и то же.
А второе доказательство - это на самом деле то же самое доказательство, но изложенное более кратко.

[Alexey1]

Цитата:

RIP
но, вообще-то, это одно и то же.

Что это?

[RIP]

"$\lim f_n(x)=f(x)$ поточечно" --- это то же самое, что "$\lim f_n(x)=f(x)$, $x\in[0;1]$" (в нашем случае).

[Alexey1]

RIP в сообщении #241293 писал(а):

... (в нашем случае).

А вот почему? Вот что не понятно.

[RIP]

Потому, что "поточечно" означает "в каждой точке рассматриваемого множества".

-- Пн 07.9.2009 21:41:27 --

Короче, насколько я понял то, что Вы написали, то делают так.
При любых $m,n>N$ и $x\in[0;1]$ выполнено $|f_n(x)-f_m(x)|<\epsilon$. Переходим к пределу при $n\to\infty$ (m и x фиксированы; существование $\lim f_n(x)=f(x)$ уже доказано), получаем $|f(x)-f_m(x)|\le\epsilon$ при любых $m>N$, $x\in[0;1]$.

[Alexey1]

Ну тогда получается, что поточечная сходимость подразумевает равномерную, что в общем случае не верно.