Проверила все магтческие константы, приведённые в Энциклопедии последовательностей (до порядка 10 включительно), у меня получились точно такие же. Как я уже сказала, у Чебракова они тоже совпадают. Магическая константа квадрата 11-го порядка, приведённого в книге Чабракова, равна

. Это тоже минимальная константа (меньше быть не может).
Я построила свой наименьший магический квадрат 11-го порядка из простых чисел и числа 1:
Код:
1 29 103 107 191 271 431 487 509 619 607
47 577 41 277 643 163 131 521 5 571 379
157 149 569 283 397 263 661 223 229 23 401
257 353 139 547 37 461 331 251 587 349 43
307 89 457 71 439 463 11 359 337 641 181
433 409 647 631 151 7 523 83 199 3 269
383 113 109 557 503 601 73 449 313 193 61
677 617 227 67 137 317 367 179 421 53 293
613 347 443 479 31 419 311 101 197 173 241
467 653 541 239 593 17 127 211 59 167 281
13 19 79 97 233 373 389 491 499 563 599
Наименьший квадрат 12-го порядка, как уже сказано, построен Дж. Н. Манси.
Для порядка

по моим подсчётам минимальная константа равна

(по-прежнему речь идёт о квадратах с использованием числа 1). Я сгенерировала набор из 13 строк для такого квадрата, но пока не превратила его в магический квадрат (программа выполняется довольно долго). Вот этот набор:
Код:
1 43 61 73 113 421 431 439 701 881 887 919 967
109 809 691 461 19 487 751 3 929 23 997 467 191
79 281 941 479 31 179 401 659 599 757 379 491 661
419 307 149 283 311 167 719 991 541 829 983 227 11
971 229 59 7 137 13 883 743 733 577 709 17 859
353 457 593 821 193 277 151 787 569 827 631 211 67
773 449 727 29 643 613 839 269 5 83 641 367 499
47 947 739 647 71 181 857 337 157 863 797 97 197
331 443 557 313 811 463 853 769 523 53 521 101 199
257 41 953 503 587 103 263 677 127 1019 673 163 571
293 601 389 317 907 131 409 509 563 349 937 359 173
251 683 107 241 233 607 239 547 653 397 1013 619 347
37 89 139 223 271 373 383 433 617 761 823 877 911
Интересно, что следующий квадрат, подобный квадрату Манси, то есть из последовательных нечётных простых чисел (включая число 1) может иметь порядок

. Магическая константа такого квадрата будет равна

. Мне удалось сгенерировать набор из 15 строк для построения такого квадрата. Но тоже пока не превратила этот набор в магический квадрат. Покажу и этот набор:
Код:
3 11 37 191 521 547 613 683 797 941 983 1021 1031 1103 1153
523 233 19 1091 1097 1381 397 431 1213 1069 131 619 151 109 1171
769 647 907 409 59 181 991 389 1291 467 1327 367 337 821 673
947 1423 271 7 41 149 881 643 743 977 719 761 757 283 1033
827 1061 563 509 659 379 31 499 829 577 313 733 1229 1319 107
1187 443 487 1231 823 1367 1361 383 229 1109 241 139 449 157 29
839 461 439 569 1259 1201 73 13 859 1217 661 709 929 47 359
1297 677 167 61 1303 997 751 1 179 311 1063 1277 1289 23 239
223 911 593 1151 1013 571 97 457 1409 887 1237 463 5 199 419
113 739 607 919 373 401 641 353 211 883 293 937 877 1039 1249
1163 1279 1009 433 269 953 617 277 163 503 137 1093 1307 101 331
1019 1051 83 197 863 1321 1087 173 17 631 263 773 307 727 1123
103 491 421 227 1129 587 967 541 691 281 1223 857 601 1427 89
971 479 1193 67 1049 853 71 1373 193 349 251 1399 1181 127 79
1301 43 317 557 257 53 1117 701 653 811 347 809 1283 787 599
Следующие порядки квадратов, подобных квадрату Манси, могут быть такими:

(магическая константа

),

(магическая константа

),
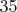
(магическая константа

). Дальше я не считала.
maxal, я не понимаю, что написано в статье по указанной вами ссылке. Вы пишете, что приведённая в этой статье последовательность минимальных магических констант квадратов порядков 3 - 10 нуждается в подтверждении. После всего сказанного мной выше, очевидно, что эта последовательность уже не может быть улучшена. Но она может быть продолжена, уже сейчас в неё можно добавить две магические константы. Таким образом, последовательность будет такой:

. Следующий член, возможно, будет

(для квадрата 13-го порядка).



