1) Поскольку глобальный максимум (наибольшее значение) непрерывной функции на некомпактном подмножестве плоскости может не существовать, следует использовать супремум (точную верхнюю грань). (Теховские коды: \max, \min, \sup, \inf:
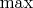
,
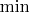
,

,

.)
2) Поскольку линия

у нас получилась в результате гомеоморфизма

, то её нельзя задать уравнением вида

. Из-за этого

не обязана быть непрерывной функцией.
Здесь действительно необходимо исправиться, хотя большой ошибки не было. Если максимума не существует, то искомая линия

есть отрезок, проходящий в точку

.
Какая "линия

"? Которую Вы хотите "провести" "между" семействами
А и
Б? Если речь идёт о моих семействах
А и
Б (точнее, о тех семействах, которые будут построены после гомеоморфизма половины сектора на весь сектор), то

ни в коем случае не будет прямолинейным отрезком. Обосновывать сейчас не буду.
А исправить надо так:

. В предыдущем посте так же исправил.
Если наша линия, полученная гомеоморфизмом половины сектора на весь сектор, такова, что

не существует, то получим

.
Что касается непрерывности

, то она не требуется. Достаточно лишь монотонности, которая обеспечена определением функции. Функция будет кусочно непрерывна.
Поскольку Вы утаили свои дальнейшие действия, мне не ясно, будет ли этого достаточно.
Да не было там никакого "предъявления". Был только очередной список пожеланий.
Был список требований, который очевидно выполним.
Не очевидно.
Если, например, я требую, чтобы линия была перенесена с одного места на другое так, чтобы заканчиваться в точке

, то такой перенос существует.
Вы можете требовать чего угодно. Однако Ваши требования не обязаны исполняться. Предъявите построение со всеми необходимыми доказательствами, если собираетесь этим гомеоморфизмом пользоваться.
Ну, если линия

, представляющая семейство
Б, является прямолинейным отрезком, то можно. Но мне хотелось бы посмотреть на построение линий

в Вашем исполнении. Я пока ни одного Вашего аккуратного доказательства не видел, поэтому мне любопытно.
Что значит аккуратное доказательство?
Это означает, что Вы определяете все необходимые объекты и доказываете, что они обладают требуемыми свойствами, а не просто составляете список пожеланий.
Пусть даны линии

-<

,

. Считаем, что

- функция:
![$l_{\nu}: [0, 1] \to (0, \frac{\pi}{2})$ $l_{\nu}: [0, 1] \to (0, \frac{\pi}{2})$](https://dxdy-01.korotkov.co.uk/f/8/9/d/89d4e8fa9047d627746e6c1761f6a7a582.png)
,

- прямой отрезок, т.е. считаем

есть функция

. Замечу, что для каждого

можно считать

, если необходимо, заменяя функции на эквивалентные. Пусть

, и

для

, где

точка минимума функции

. Функция

монотонна, возрастает при росте

. Тогда по функции

берём гладкую функцию

такую, что

-<

-<

. Подробности процедуры, действительно, не даю. Кроме того, построив

строим

с тем дополнительным условием, чтобы было ещё

-<

. И вообще, если построены линии

для

, то линию

строим с теми условиями, что:

-<

-<

и, одновременно,

-<

для всех

.
Раз уж Вы сказали, что

, то ещё следовало сказать, что

(это единственный интересный случай) и определить

без всякой возни с минимумами, которых может быть много или, наоборот, ни одного.
Условия выполнимы, так как на каждом шаге строится не более чем счётное количество линий.
Выполнимы, конечно, но вдруг кому-нибудь это не очевидно? Я не в счёт, я такими построениями занимался (в качестве учебной задачи) лет 40 назад (ну, чуть поменьше), когда учился на третьем курсе.
Кроме того, сведение задачи к другой задаче, с которым разбираемся, оказывается вовсе не обязательно.
Я, вообще-то, всё время удивлялся: зачем это сведéние нужно? Но хозяин - барин, доказательство-то Ваше. Свести можно, только пользы от этого не видно. Да и зачёт по этому сведéнию Вы не сдали, так что к экзамену по доказательству Вас можно не допускать.
Ладно, забываем про это сведéние и возвращаемся к исходным семействам
А и
Б.
Семейство
Б состоит из одной линии

, заданной уравнением

, а семейство
А построено
здесь.
Для построения мне понадобятся вспомогательные непрерывные функции

,

,

, которые я определю так:

а при


Заметим, что на каждом отрезке
![$\left[1-\frac 1k,1-\frac 1{k+1}\right]$ $\left[1-\frac 1k,1-\frac 1{k+1}\right]$](https://dxdy-04.korotkov.co.uk/f/f/0/d/f0dd52f9f09d160cc63acedaf55f028882.png)
в точности две из этих функций отличны от

, а именно,

и

, причём, их сумма на этом отрезке равна

. Поэтому, в частности, ряд

сходится на полуинтервале

, и его сумма равна

.
Кроме того, каждая точка

имеет окрестность, в которой отличны от

не более трёх из этих функций (для точки

годится полуинтервал

; если точка принадлежит интервалу

, то годится сам этот интервал; если точка совпадает с

при

,

, то годится

).
Теперь надо построить семейство
А, указанное в приведённой выше цитате из моего
сообщения. Для этого, разумеется, достаточно указать непрерывные функции

,

. Используем построение по индукции по всем ординалам, меньшим

.
Предположим, что для некоторого ординала

уже построены непрерывные функции

,

, удовлетворяющие следующим условиям:
а) для всех

выполняются неравенства

при

, и существует

;
б) если

, то найдётся такое число

, что при всех

выполняется неравенство

.
(Для

множество функций будет пустым.)
Построим

. Рассмотрим три случая.
1) Для

положим

. Заметим, что эта функция непрерывна и

при

, и

, то есть, условие а) выполняется, а условие б) тривиально.
2) Ординал

- не предельный, то есть, существует такой ординал

, что

. Тогда положим

. Эта функция непрерывна, так как по предположению индукции

непрерывна.
Условие а) выполняется:
так как при

по предположению индукции

, то

, то есть,

;
так как

, то

.
Условие б) выполняется:
так как при

выполняется неравенство

, то

;
если задан ординал

, то по предположению индукции найдётся такое число

, что при всех

выполняется неравенство

. Тогда для этого

и

получим

.
3) Ординал

- предельный. Перенумеруем все ординалы, меньшие

, натуральными числами. Таким образом, все ординалы, меньшие

, перечислены в виде последовательности

. Для каждого

и

положим

. Сразу заметим, что эти функции непрерывны на

, и при

выполняются неравенства

.
Определим функцию

. Эта функция непрерывна на

, так как члены этого ряда непрерывны, и для каждой точки рассматриваемого полуинтервала существует окрестность, в которой отличны от

не более трёх членов ряда. Заметим, что при

на отрезке
![$\left[1-\frac 1n,1-\frac 1{n+1}\right]$ $\left[1-\frac 1n,1-\frac 1{n+1}\right]$](https://dxdy-03.korotkov.co.uk/f/2/3/4/234097ca7b29823468fc0b0115fbf61a82.png)
выполняются неравенства
то есть,

. Поскольку

можно взять произвольным, неравенство

выполняется при всех

.
Наконец, положим

. Эта функция непрерывна. Проверим, что выполняются условия а) и б).
Условие а):
так как при

имеем

, то

, то есть,

;
так как

и

при

, то, по теореме о двух милиционерах,

, откуда

.
Условие б):
пусть

; существует такое

, что

. Тогда при

из неравенства

получаем

, то есть,

при

.
Таким образом, требуемая функция

построена, и можно продолжать построение дальше.
Требуемое семейство
А, таким образом, построено.
Поскольку Вы хотите иметь также монотонность и гладкость, немного продолжим рассуждения.
Сначала докажем (по индукции), что построенные функции

,

, являются возрастающими на

.
1) Для

функция

(определена в цитате в пункте 1)), разумеется, возрастающая.
Предположим, что для ординала

доказано, что при всех

функция

возрастающая. Докажем, что и

возрастающая.
2) Ординал

не предельный. Тогда существует такой ординал

, что

. Функция

- возрастающая по предположению, поэтому и

(определена в цитате в пункте 2)) возрастающая.
3) Ординал

предельный. Все определения приведены в цитате в пункте 3). По предположению, все функции

,

, являются возрастающими. Поэтому возрастающими являются и функции

.
Теперь докажем, что и функция

возрастает на

. Достаточно проверить, что она возрастает на каждом отрезке
![$\left[1-\frac 1n,1-\frac 1{n+1}\right]$ $\left[1-\frac 1n,1-\frac 1{n+1}\right]$](https://dxdy-03.korotkov.co.uk/f/2/3/4/234097ca7b29823468fc0b0115fbf61a82.png)
,

, так как эти отрезки покрывают весь полуинтервал

. Из перечисленных выше свойств функций

,

, следует, что на данном отрезке выполняется равенство

(все остальные члены ряда на данном отрезке обращаются в

).
Возьмём любые две точки

, удовлетворяющие условию

. Докажем, что

.
для краткости обозначим

и

. Из свойств функций

,

, следует, что выполняются условия

и

. Тогда
так как все три слагаемых в последнем выражении неотрицательны, причём, последнее положительно (функция

возрастающая,

). Поэтому

, то есть, функция

возрастает на каждом отрезке
![$\left[1-\frac 1n,1-\frac 1{n+1}\right]$ $\left[1-\frac 1n,1-\frac 1{n+1}\right]$](https://dxdy-03.korotkov.co.uk/f/2/3/4/234097ca7b29823468fc0b0115fbf61a82.png)
,

, а потому и на всём полуинтервале

.
Наконец, из определения функции

следует, что она также возрастает на

.
Поэтому делаем вывод, что все функции

,

, являются возрастающими.
Теперь разберёмся с гладкостью. Для действительных чисел

,

, определим функцию

(здесь

- одно из распространённых обозначений показательной функции). Подобные функции иногда используются, когда нужно гладко "сшить" две константы, поэтому будем считать известным, что эта функция бесконечно дифференцируема на всей числовой оси (это проверяется стандартными вычислениями с использованием определения производной в точках

и

), причём,

при всех

. Кроме того, при

получаем

так что эта функция возрастает на отрезке
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
.
1) Заметим, что функция

бесконечно дифференцируема на

.
Пусть

. Предположим, что для всех

бесконечно дифференцируемые возрастающие функции

, удовлетворяющие указанным в цитате условиям а) и б), уже построены.
2) Если ординал

не предельный, то определяем функцию

как в процитированном построении, и её бесконечная дифференцируемость на

следует из бесконечной дифференцируемости

.
3) Если ординал

предельный, то, по сравнению с процитированным выше построением, в изменении нуждается только определение функции

, а все вспомогательные функции определяются так же.
Для

определим

. Заметим, что при

выполняются неравенства

, так как эта функция возрастающая.
Определим теперь функцию

при

,

, равенством

. Эта функция на полуинтервале

по построению возрастает, бесконечно дифференцируема (в "сомнительных" точках

,

, все производные равны

в силу свойств функции

) и удовлетворяет неравенству

. Все остальные требуемые свойства проверяются так же, как в процитированном выше построении.
Таким образом, функции с требуемыми свойствами построены. Заметим, что их все можно доопределить в точке

по непрерывности, положив

,

. При

функции

будут бесконечно дифференцируемыми на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Что касается функций

при

, то можно доказать, что существует

, но непрерывности производной в точке

, скорее всего, не будет. Тем более не следует ожидать существования в этой точке производных высших порядков.
Вообще, условия монотонности и гладкости функций

,

, ввиду ожидающихся далее построений, выглядят для меня как бантик на паровозе: красиво, пока не закоптился, и абсолютно бесполезно. Поэтому я дальнейших усилий в этом направлении прилагать не буду. Если Вам позарез нужно, заботьтесь об этом далее сами.
Итак, что там у нас на очереди? Построение деформаций, "разводящих" линии? Прошу Вас, предъявите такую деформацию

для

. Больше пока не надо. Прежде, чем делать что-либо дальше, нужно разобраться с первым шагом.
Это метод его конструкции.
Ладно, Вы (и, может быть,
AGu, если захочет) разбирайтесь с его "гипердействительными" числами, а я буду возиться с топологией.



