Тренировки ради взялся попереводить аннотации свежих статей с
http://ru.arxiv.org/list/math.NT/recent. Подскажите, пожалуйста, где у меня есть ошибки.
О распределении значений дзета-функции Римана на критической прямой
Юстас Калпокас, Йорн Стойдинг
http://ru.arxiv.org/abs/0907.1910В работе исследуются точки пересечения кривой

с действительной осью. Мы показываем, что если гипотеза Римана верна, то центр масс таких точек существует и попадает в 1. Далее, без привлечения дополнительных предположений, показано, что дзета-функция принимает сколь угодно большие значения на критической прямой.
О числе различных простых делителей чисел вида

Хао Пан
http://ru.arxiv.org/abs/0907.1940Пусть

обозначает количество различных простых делителей

. Тогда для любого большого

, малого

и достаточно большого (зависящего только от

и

) действительного

, существует по крайней мере

целых чисел
![$n\in[x,(1+K^{-1})x]$ $n\in[x,(1+K^{-1})x]$](https://dxdy-01.korotkov.co.uk/f/0/c/2/0c2b63583585a337b45c4cca7a7de24382.png)
таких, что неравенство

выполнено для всех

и

.
Некоторое улучшение оценок сумм/произведений в полях простого порядка
Лиангпан Ли
http://ru.arxiv.org/abs/0907.2051Пусть

- поле вычетов по модулю

и пусть

- непустое подмножество

. В данной статье мы показываем, что если

, то

; если

, то

. Эти результаты несколько улучшают оценки Бургена-Гараева и Шеня. Также приводятся оценки сумм/произведений для различных множеств.
Невырожденные кривые малого рода над малыми конечными полями
Вутер Кастрик, Джон Войт
http://ru.arxiv.org/abs/0907.2060В предыдущей статье мы доказали, что над конечным полем

достаточно большой мощности все кривые, род которых не превосходит 3 над

, могут быть промоделированы полиномом Лорана от двух переменных, которые невырожден в смысле своего политопа Ньютона. В данной статье мы доказываем, что существует ровно 2 невырожденных кривых, род которых не превосходит 3 над конечным полем, одна - над

и одна - над
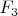
. Обе эти кривые обладают замечательными экстремальными свойствами, касающимися количества рациональных точек над различными полями расширений.
Характеризация алгебраических кривых с бесконечным числом целых точек
Юри Билу, Альванос Параскевас, Поулакис Димитриос
http://ru.arxiv.org/abs/0907.2097Классическая теорема Зигеля утверждает, что множество

-целых точек на алгебраической кривой

над числовым полем конечно, если только род

отличен от 0 и кривая имеет не более двух бесконечно удаленных точек. В данной статье мы приводим необходимые и достаточные условия нахождения на кривой

бесконечного числа

-целых точек.
Многоликая теорема о подпространствах
Юри Билу
http://ru.arxiv.org/abs/0907.2098В течение последнего десятилетия были найдены несколько весьма неожиданных приложений теоремы о подпространствах, в основном - в диофантовом анализе и теории трансцендентности. Из массы впечатляющих результатов я отобрал те, в которых возникает меньше технических трудностей и которые позволяют оценить, как изящно теорема о подпространствах используется при решении сложных проблем, которые вряд ли кто-либо рассчитывал разрешить так просто. Три главных темы статьи - это: работа Адамчевского и Бюжо о сложности алгебраических чисел; работы Корвая и Занниера о диофантовых уравнениях со степенными суммами и о целых точках на кривых и поверхностях; а также дальнейшие исследования Левина и Отиссира. В частности мы приводим полное доказательство прекрасной теоремы Левина и Отиссира: аффинная поверхность с четырьмя или более соответственно пересекающимися на бесконечности обильными дивизорами не может иметь плотное по Зарисскому множество целых точек.
О дробях Фарея с нечетными знаменателями
Алан К. Хейнес
http://ru.arxiv.org/abs/0907.2168В данной статье мы рассматриваем дроби Фарея порядка

с нечетными знаменателями. В частности, мы обсуждаем частоты значений числителей разностей последовательных элементов в этом множестве. После получения соответствующего асимптотического соотношения, мы используем оценки неполных сумм Клоостермана, чтобы обобщить наш результат на подынтервалы отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
.
Распределение подмножеств последовательности Фарея специального вида
Алан К. Хейнес
http://ru.arxiv.org/abs/0907.2171В данной статье мы обобщаем некоторые результаты из нашей "О дробях Фарея с нечетными знаменателями" на подмножества дробей Фарея, знаменатели которых не делятся на заданное простое число. Мы также исследуем совместное распределение числителей разностей

-кортежей последовательных дробей в этих множествах.