Неравенство

[arqady]

Для положительных $a,$ $b$ и $c$ докажите, что

$$\frac{a^3+b^3+c^3}{ab+ac+bc}+\frac{4abc}{a^2+b^2+c^2}\geq\frac{7}{9}(a+b+c)$$

[meduza]

А подсказку можно?

[arqady]

meduza в сообщении #225243 писал(а):

А подсказку можно?

Можно, конечно! Только имеются, видимо, несколько подходов...
В доказательстве, которое мне удалось найти, существенно используется, что $(a-b)^2(a-c)^2(b-c)^2\geq0.$

[Sasha2]

Да, очень злое неравенство. Ничего, честно говоря в голову не приходит.
Хотя, наверно ведь можно использовать то, что оно симметрично по всем параметрам.
То есть без ограничения общности можно считать, что a не больше b, которое в, свою очередь не больше c. То есть полжить b=a*x и с=a*y, где x и y - оба больше единицы. Тогда хоть удастся свести к двум переменным. Попробую, может чего-нибудь получиться.

[meduza]

Sasha2 в сообщении #225391 писал(а):

Хотя, наверно ведь можно использовать то, что оно симметрично по всем параметрам.

Я попытался использовать методы, описанные в [1], но, к сожалению, получившееся неравенство стало еще страшнее:

$$\dfrac{\sigma_1^3-3 \sigma_1 \sigma_2 + 3\sigma_3}{\sigma_2}+\dfrac{4 \sigma_3}{\sigma_1^2-2\sigma_2}\geqslant \dfrac{7}9 \sigma_1$$

где $\sigma_1=a+b+c$, $\sigma_2=ab+bc+ac$, $\sigma_3=abc$. Упростить его до легкорешаемого неравенства мне не удалось

[1] Болтянский В., Виленкин Н., Симметрия в алгебре.

[Sonic86]

Напрямую решается, но некрасиво и довольно трудоемко. Для этого надо перейти к симметрическим многочленами $\sigma_j$, затем, в силу однородности, удобно сделать замену $x=\frac{\sigma_2}{\sigma_1 ^2}, y=\frac{\sigma_3}{\sigma_1 ^3}$, и тогда слева получится квадратичная форма (гиперболический параболоид), у которой в 1-й четверти будет область отрицательных значений. Но поскольку $a,b,c$ - действительные корни кубического уравнения, то на $x,y$ накладывается ограничение $D \leq 0$, которое надо предобразовать в ограничение на $x,y$ (не так давно пост был про универсальный метод решения симметрических неравенств, идея оттуда). Построив обе кривые на плоскости видно, что области, где $D \leq 0$ и где квадр форма принимает отрицательные значения, не пересекаются. Если еще границу учитывать - будет 1 точка пересечения, соотвествующая случаю $a=b=c$. 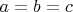(в принципе параболу Нейля там можно очень хорошо аппроксимировать 2-я отрезками прямых и доказать неравенство после этого алгебраически с помощью матанализа, но неохота, все равно идеи нету).

З.Ы. С другой стороны, неравенство так легче обобщить - найти семейство парабол, касающихся острия параболы Нейля, и их уравнение обратно преобразовать в симметрическое неравенство (хотя оно, наверное, тоже некрасивое получится).

[Sasha2]

To Meduza

Вы знаете, я не знаком еще с этими симметрическими многочленами.
А посмотрите пожалуйста, вот что получится если сперва использовать в иссходном неравенстве
вот такое разложение:

$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)$

P.S. За источник спасибо, уже скачал. Буду ознакамливаться.

[Sasha2]

Вот не поленился и перемножил все, затем вычел из левой части правую и вот, что получилось

$9(a^5+b^5+c^5)+2(a^2b^3+a^3b^2+a^2c^3+a^3c^2+b^2c^3+b^3c^2)-7(a^4b+ab^4+a^4c+ac^4+b^4c+bc^4)+22(a^2bc^2+a^2b^2c+ab^2c^2)-21(a^3bc+ab^3c+abc^3)$

Возникает такой вопрос, если неравенство истинное, то означает ли это, что данное выражение может быть преобразовано к сумме произведений некоторых членов и их степеней на квадраты отдельных кусков, ну что-типа $a^3(a-b+c)^2$

И еще, возможно ли такое разложение так, чтобы коэффициенты были целыми?

-- Вт июн 30, 2009 15:54:26 --

Вот еще интересно, что если пытаться искать разложение в виде
$9(a^3+b^3+c^3)(a^2+b^2+c^2-ab-bc-ac)$,
так вот если вычесть это из того, что приведено чуть выше, то неравенство (уже при равных числах нарушается).
Тоньше однако разнича чем $(a^2+b^2+c^2-ab-bc-ac)$

[arqady]

Sasha2 в сообщении #225703 писал(а):

Вот не поленился и перемножил все, затем вычел из левой части правую и вот, что получилось

$9(a^5+b^5+c^5)+2(a^2b^3+a^3b^2+a^2c^3+a^3c^2+b^2c^3+b^3c^2)-7(a^4b+ab^4+a^4c+ac^4+b^4c+bc^4)+22(a^2bc^2+a^2b^2c+ab^2c^2)-21(a^3bc+ab^3c+abc^3)$

Возникает такой вопрос, если неравенство истинное, то означает ли это, что данное выражение может быть преобразовано к сумме произведений некоторых членов и их степеней на квадраты отдельных кусков, ну что-типа $a^3(a-b+c)^2$

Если известно что

$$\sum_{cyc}(9a^5-7a^4b-7a^4c+2a^3b^2+2a^3c^2-21a^3bc+22a^2b^2c)\geq0,$$

то, конечно, можно! Например, так:

$$\left(\sqrt{\sum_{cyc}(9a^5-7a^4b-7a^4c+2a^3b^2+2a^3c^2-21a^3bc+22a^2b^2c)}\right)^2\geq0.$$

Ежели Вы имете в виду, всегда ли можно положительно определённый симметрический многочлен от нескольких переменных с целыми коэффициентами представить как сумму квадратов многочленов с действительными коэффициентами, то ответ - нет, не всегда.
Можно, правда, получить что-то такое:

$$\sum_{cyc}(9a^5-7a^4b-7a^4c+2a^3b^2+2a^3c^2-21a^3bc+22a^2b^2c)=\frac{1}{2}\sum_{cyc}(a-b)^2S_c,$$

где $S_c=9a^3+4a^2b+4ab^2+9b^3-c^3-22abc.$
Буду рад, если это Вам поможет.

[Sasha2]

Нет я не утверждал, что в виде суммы квадратов, а виде суммы произведений кусков заведомо положительных.
Вообще я не очень понимаю, как такое доказывается, но вот попробовав выше я понял, что
1) Все такие симметрические многочлены достигают своих экстремальных значений (если таковые есть в симметричной же точке, ну что-то типа a=b=c).
2) Взяв какой-либо кусок, а многочленов-то вообщем то не очень много, ну вот как у меня выше $9(a^3+b^3+c^3)(a^2+b^2+c^2-ab-bc-ac)$ надо сопоставить сумму произведений коэффициентов на число слагаемых при этих коэффициентах, как в группу положительных, так и в группе отрицательных слагаемых. Если отрицательных больше, значит забрали в положительный кусок больше, чем следует. Ну в смысле, не удасться провести оценку.
3) Ваше тождество, конечно, спасибо, но оно явно не поможет, в смысле одно оно само по себе не говорит, что этот кусок положительный.

[arqady]

Sasha2 в сообщении #225770 писал(а):

попробовав выше я понял, что
Все такие симметрические многочлены достигают своих экстремальных значений (если таковые есть в симметричной же точке, ну что-то типа a=b=c).

Это неверно! Многочлен

$$\sum_{cyc}a(a-b)(a-c)(a-2b)(a-2c)$$

при неотрицательных $a,$ $b$ и $c$ достигает своего наименьшего значения в семи сериях точек и только одна из них, а именно $(t,t,t)$ является "симметричной", как Вы говорите.

Sasha2 в сообщении #225770 писал(а):

3) Ваше тождество, конечно, спасибо, но оно явно не поможет, в смысле одно оно само по себе не говорит, что этот кусок положительный.

По моему, неположительность "куска" не даёт основание браковать всё рассуждение.
Например, при доказательстве неотрицательности $\sum_{cyc}(a^3-a^2b-a^2c+abc)$ при неотрицательных $a,$ $b$ и $c$ его представление в виде $\sum_{cyc}(a-b)^2S_c$ очень даже помогает. Попробуйте!

[Sasha2]

Оно все рассуждение браковать не дает, но сам один кусок не позволяет сделать заключение, нужно его заведомо отрицательную часть скомбинировать с некоторыми частями из других кусков. Я это и имел в виду.
Ну Вы по сути дела уже и все решение высказали.
Я еще поробую по своему. А именно. Разница между частями неравенства - это многочлен пятой степени. Поэтому, особо там не наконструируешь из симметрических многочленов.

А вот еще такой вопрос. Вот, как Вы интересно конструируете такие неравенства.
Точнее, как конструируют, я догадываюсь берут наверно произвольную рациональную однородную дробь (заведомо неотрицательную в области неотрицательных значений) и подставляют туда какую-либо линейную комбинацию симметрических многочленов в качестве аргумента. ну и преобразуя потом, получают то что мы решаем.

А вот так на вскидку, если слегка поменять коэффициенты в Вашем задании (сокранив симметрию), но вопрос поставить по другому, а именно ОЦЕНИТЕ СНИЗУ левую часть выражением k*(a+b+c). То есть найти то k, при котором неравенство верно для всех положительных a, b и с или доказать что такого k не существует. Вот как в таком случае действовать?

Я еще вот попробую завтра, я уже с ним столько провозился, оно у меня уже в башке сидит.
Почему то, кажется, что эта разница между левой и правой частью должна быть равна (хотя, конечно, нужно проверить)

$m*(a+b+c)*(a^2+b^2+c^2-ab-ac-bc)^2 + n*abc*( a^2+b^2+c^2-ab-ac-bc)$

Ну или около того

где m и n, еще нужно определить.

[arqady]

Sasha2 в сообщении #225792 писал(а):

Ну Вы по сути дела уже и все решение высказали.

Отнюдь. Мне как раз не удалось его доказать этим путём.

Sasha2 в сообщении #225792 писал(а):

А вот еще такой вопрос. Вот, как Вы интересно конструируете такие неравенства.

Наше неравенство получилось так.
Очевидно для положительных $a,$ $b$ и $c$ выполняются следующие неравенства:
$\frac{a^3+b^3+c^3}{ab+ac+bc}\geq\frac{a+b+c}{3}$ и $\frac{abc}{a^2+b^2+c^2}\leq\frac{a+b+c}{9}.$
Оказывается, для наибольшего $k,$ при котором неравенство

$$\frac{a^3+b^3+c^3}{ab+ac+bc}+\frac{3kabc}{a^2+b^2+c^2}\geq\frac{1+k}{3}(a+b+c)$$

выполняется для всех положительных $a,$ $b$ и $c$ должно выполняться

$$k\leq\min_{t>0}\frac{(3t+4)(t^2+2)}{(t+4)(2t+1)}=1.34...$$

При $k=\frac{4}{3}$ получаем наше неравенство. Остаётся его доказать, что и было сделано. Кстати, у этого неравенства есть очень простое доказательство, которое я сразу не увидел. meduza своим постом подсказал
То, что $1.34...$ удалось приблизить простым рациональным числом - это дело случая и удачи.
Попробуйте сами - и Вы быстро убедитесь, что получаются в основном громоздкие или хорошо известные неравенства.

[Sasha2]

Вот весь день делил остаток на (a+b+c) и вот, что получилось
$(a+b+c)[9(a^4+b^4+c^4)-16(a^3b+ab^3+a^3c+ac^3+b^3c+bc^3)+18(a^2b^2+a^2c^2+b^2c^2)-80(abc^2+a^2bc+ab^2c)]+164(a^2b^2c+a^2bc^2+ab^2c^2)+91(a^3bc+abc^3+ab^3c)$

А дальше честно, говоря деление приводит к тем же степеням, которые уже были.
Можно до бесконечности делить. Значит такой способ не приводит к цели.

[Sasha2]

Вот получил методом полунаучного тыка еще вот такое неравенство
$3abc(a+b+c)\geq4(ab+bc+ac)^2-(a+b+c)^2(ab+bc+ac)$

Подставил его в исходное и опять ничего. Проверил для a=1, b=2 и c=3.
Уже нарушается.
Аркадий, может все таки покажете решение, а то уже не знаю прямо куда копать.