Для

, кажется, все будет еще проще, чем для предела: достаточно просто убрать условие "для всех достаточно больших k ...", т.е. "существует n, такое что при всех

...". Соответственно, не будет последнего пересечения по

, и останутся только два объединения:

Попробуйте доказать эту формулу по аналогии с доказательством из Колмогорова-Фомина для предела.
Насчет функции
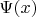
, наверное проще будет просто поменять знаки неравенств в другую сторону (при этом

, разумеется, нужно будет прибавлять, а не вычитать).