Дима Тишков писал(а):
Вообще, без проблем можно доказать возможность выбора из любого конечного семейства множеств (непустых и попарно непересекающихся конечно), просто взяв и объединив в множество по одному элементу из каждого.
Мне больше нравится версия аксиомы выбора, в которой под "выбором" из семейства

понимается не множество, пересекающееся с каждым

по одному элементу, а семейство

такое, что

для всех
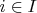
. (В этом случае нет необходимости требовать, чтобы

попарно не пересекались.) Но это дело вкуса. И я, собственно, не из-за этого встрял. Тут вот какое дело...
В цитированной выше идее есть некая (чисто формальная) бяка. Доказать-то это можно, но все же не "просто взяв и объединив". При таком лобовом подходе длина доказательства существования выбора будет зависеть от числа членов заданного конечного семейства. (Кстати, я здесь намеренно написал "заданного", ибо для произвольных конечных семейств такой подход вообще не имеет смысла. Но это так, формализаторство.) А доказательство нужно одно, общее для всех конечных семейств сразу.
Так что я все же предлагаю несколько секунд подумать над доказательством того, что "для любого конечного семейства непустых множеств существует выбор". (Да, без аксиомы выбора. И да, это действительно легко.)



