Brukvalub писал(а):
Например, при соизмеримости периодов.
это утверждение можно до некоторой степени обратить.
рассмотрим функцию

непрерывную на всей плоскости и она
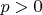
-периодична по

и

-периодична по

.
Предположим, что при некотором фиксированном

эта функция

-периодична по

и при ннекотором фиксированном

она

-периодична по

. Берутся минимальные периоды.
Тогда если числа

и

рационально несоизмеримы то функция

не имеет периодов отличных от нуля.
с соответствующими выводами относительно сумм и произведений:

и тп



