Нет, не "в обозначениях" -- я имел в виду не

, а именно

.
В теории волн скорость волн обычно обозначается

для любой природы волн, при наличии дисперсии, нелинейности и т. п. Вы, видимо, настаиваете на обозначении

чтобы не путать со скоростью света. Это излишне.
Преобразования что Лоренца, что Галилея -- вещь в известном смысле тривиальная, и на общих свойствах решений, связанных с дальнодействием, не отражается.
Мягко говоря, вообще не всякие волны инвариантны относительно хотя бы каких-то симметрий. Например, волны на воде - не подчиняются ни Лоренцу, ни Галилею.
К физике, конечно, отношения никакого не имеет, но.
(тег испортился?)
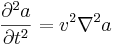
Пользуйтесь
http://www.sciencesoft.at/index.jsp?link=latex&lang=en как запасным аэродромом.
Это уравнение по вашему конкретное или нет?
Батенька, так до предела уравнение одно, после предела другое, а "в пределе" - это как раз не конкретное уравнение, а, например, последовательность уравнений. Тщательне́й надо.
Добавлено спустя 2 минуты 25 секунд:Ничего мы не имеем. При стремлении какого угодно параметра к чему угодно можно разве что отследить некоторое асимптотическое поведение решения, однако финитность ни в какую асимптотику не вкладывается -- она или есть при фиксированных значениях параметра, или её нет.
Корректнее надо сказать, что наличие финитности - разрывная функция ровно в точке взятия предела :-)



