Тензор трансформации?

[t3rmin41]

Не знал, как назвать тему (собственно, поэтому и стоит знак вопроса).

А теперь сама проблема:

как известно, в геометрической оптике угол падения и угол отражения луча равны, если они лежат в одной плоскости с перпендикуляром, от которого отсчитываем углы.

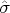
Пускай имеем падающий луч $ \vec{r}=r_x\vec{i}+r_y\vec{j}+r_z\vec{k} $ тогда отражённый луч будет $ \vec{r'}=r'_x\vec{i}+r'_y\vec{j}+r'_z\vec{k} =-r_x\vec{i}-r_y\vec{j}-r_z\vec{k} $. Линейная операция, которая трансформирует луч $ \vec{r} $ в $\vec{r'}$, я так понимаю, может быть записана как $ \vec{r'} = \hat\sigma \vec{r} $ где $\hat\sigma$ - тензор трансформации.

На мой взгляд, этот тензор может быть получен уравнением

$ \hat\sigma = \sigma E$, $E$ - единичная матрица $3\times3$, $\sigma = -1$ (смысл операции отражения).

Вопрос - правильно ли получен тензор? Можно ли по аналогии с этим тензором определять другие линейные тензоры, переводящие один вектор в другой?

[Утундрий]

Тензор написан неправильно, что следует уже хотя бы из того, что в конструкции данного тензора никак не участвуют параметры, характеризующие положение относительно луча отражающей плоскости.

[t3rmin41]

Может быть, он сконструирован и неправильно, но ведь он, так скажем, "работает". Так почему же он написан неправильно?
И если он сконструирован неправильно, то как вообще составляются тензоры?

[Munin]

Тензоры можно составить из векторов, тензорным произведением. Никак не могу запомнить, как его обозначают безкоординатно, пусть будет $\otimes.$ Тогда простейший вариант $\mathbf{a}\otimes\mathbf{b}$ будет означать следующее: проекция пространства на ось $\mathbf{b},$ и поворот её в положение $\mathbf{a},$ с некоторым растяжением (из модулей векторов). Любой тензор преобразования (transform) можно представить себе как сумму трёх (по числу измерений пространства) таких простейших вариантов: $T=\mathbf{a}_1\otimes\mathbf{b}_1+\mathbf{a}_2\otimes\mathbf{b}_2+\mathbf{a}_3\otimes\mathbf{b}_3.$

Отсюда должно быть уже понятно, как сделать тензор отражения от плоскости. Он должен быть суммой двух частей: проекция на плоскость и проекция на перпендикуляр к плоскости. Проекцию на плоскость надо взять со знаком $+1,$ а проекцию на нормаль - со знаком $-1.$ Если $\mathbf{i},\mathbf{j}$ и $\mathbf{k}$ - орты, причём $\mathbf{k}$ нормален к плоскости отражения, то получается $T=\mathbf{i}\otimes\mathbf{i}+\mathbf{j}\otimes\mathbf{j}-\mathbf{k}\otimes\mathbf{k}.$

[t3rmin41]

Я надеялся, что Munin увидит эту тему и отпишет в ней :]
Спасибо, буду разбираться. Только я слышал про скалярное и векторное произведения, а вот про тензорное - нет. Что ж, надо посмотреть, что это такое.

[Munin]

t3rmin41 в сообщении #186315 писал(а):

Я надеялся, что Munin увидит эту тему и отпишет в ней :]

Коварно :-)

t3rmin41 в сообщении #186315 писал(а):

Только я слышал про скалярное и векторное произведения, а вот про тензорное - нет.

Просто скалярное и векторное изучают в векторном анализе, а тензорное нет :-) Кажется, для данного случая оно ещё называется прямое, хотя я могу путать. Намного проще всё это в знакомых индексных обозначениях: $T^{i}{}_{j}=a^{i}b_{j}.$

А ваша изначальная матрица $\mathop{\mathrm{diag}}(-1,-1,-1)$ - это не отражение от плоскости, это отражение относительно точки, меняющее любой вектор на направленный ровно в обратную сторону. От плоскости так луч света не отражается, только от катафота (световозвращателя).

[t3rmin41]

Munin писал(а):

t3rmin41 в сообщении #186315 писал(а):

Я надеялся, что Munin увидит эту тему и отпишет в ней :]

Коварно

Да нет, никакого коварства :] Зная ваши предыдущие ответы, только в том случае, если бы отписали вы, я мог бы ещё что-то понять и уяснить, в каком направлении двигаться.

Попробовал посмотреть тензорное произведение и что такое тензор вообще, но видимо, лучше сначала начать с теории групп. Или может вы лучше бы сказали, откуда начать?
Тем более, что в ближайшем будущем, насколько я знаю свой курс, понятия тензора как "правила, по которому один вектор преобразуется в другой", должно хватить.

[Утундрий]

Вас должно было насторожить уже то, что решение явно неизотропной задачи дано в явно изотропной форме.

P.S. Теория групп тут совершенно ни при чем.

[ewert]

мне лень вскрывать все картинки, но вообще-то линейный оператор отражения стандартно описывается как $\vec r'=\vec r-2{(\vec r,\vec n)\over|\vec n|}\cdot\vec n$, где $\vec n$ -- любой из векторов нормали к отражающей плоскости.

А "тензор отражения" (один раз ко-, другой контравариантный) -- это попросту матрица того оператора в выбранном базисе.

[Jnrty]

ewert, там, наверное, в знаменателе случайно забыт квадрат ($\left|\vec n\right|^2$)?

[ewert]

да, каюся. Хотя бы из соображений размерности следует, что -- воистину забыт...

[Munin]

t3rmin41 в сообщении #186322 писал(а):

Попробовал посмотреть тензорное произведение и что такое тензор вообще, но видимо, лучше сначала начать с теории групп.

Утундрий прав, теория групп совершенно ни при чём. Тензоры - это часть линейной алгебры, следующий шаг после векторов.

t3rmin41 в сообщении #186322 писал(а):

Тем более, что в ближайшем будущем, насколько я знаю свой курс, понятия тензора как "правила, по которому один вектор преобразуется в другой", должно хватить.

Это - только один вид тензоров, один раз контравариантный и один раз ковариантный тензор, или (1,1). Применяются и многие другие. Например, тензор вида (0,2) (тоже второго ранга) даёт "правило, по которому двум векторам сопоставляется число" - то есть билинейную форму, часто используемую и как квадратичная форма.

[ИгорЪ]

Я немного занимался матричной оптикой. Сформулируйте задачу конкретно. Возможно подскажу. Тензорных произведений здесь конечно не надо - из пушки. Да и задача обычно сводится к двумерной.

[t3rmin41]

ИгорЪ писал(а):

Я немного занимался матричной оптикой. Сформулируйте задачу конкретно. Возможно подскажу. Тензорных произведений здесь конечно не надо - из пушки. Да и задача обычно сводится к двумерной.

Да тут не в задаче дело. Я просто хотел бы разобраться, как составляются тензоры как общий случай преобразования векторов, и как частный случай - тензор отражения. В принципе, Munin дал достаточно развёрнутый ответ, но если вам есть что дельного добавить - всегда пожалуйста.

[ewert]

Munin в сообщении #186318 писал(а):

а тензорное нет Кажется, для данного случая оно ещё называется прямое,

насколько я помню, тензорное произведение -- это попросту произведение компонент тензоров, с соответствующим тупо сложением рангов. Или нет?