Понять написанное Вами,
Александрович, в трех предыдущих сообщениях — невозможно. Предлагаю модификацию исходной задачи в «духе толерантных» интервалов.
0. Задача (2-я модификация). Пусть

,

,

,

— независимые,

-нормально распределенные случайные величины. Требуется построить верхний

-доверительный толерантный интервал для случайной величины

(на другом языке — доверительный интервал для квантили

уровня

распределения случайной величины

) в виде

, т.е.

.
Здесь

, где

— функция распределения случайной величины

.
1. Решение. Как уже выше
в этой теме указывалось,

, где

— функция стандартного нормального распределения. Следовательно,
![$\xi_p = u(\sqrt [N] p)$ $\xi_p = u(\sqrt [N] p)$](https://dxdy-01.korotkov.co.uk/f/c/f/9/cf9cdcc209315cc03b7352fab21c9a4582.png)
, где

— квантиль уровня

стандартного нормального распределения. Без ограничения общности можно считать, что

,

имеют
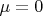
,

. По сути повторяя рассуждения примера 10.9 [8], получим
![$\lambda = \frac {t_{\gamma} [L-1, \sqrt L u(\beta)]} {\sqrt L}$ $\lambda = \frac {t_{\gamma} [L-1, \sqrt L u(\beta)]} {\sqrt L}$](https://dxdy-02.korotkov.co.uk/f/5/3/3/533fe0164b29cd68675e70190ce4dd7c82.png)
, где
![$ t_{\gamma} [L-1, \sqrt L u(\beta)]$ $ t_{\gamma} [L-1, \sqrt L u(\beta)]$](https://dxdy-04.korotkov.co.uk/f/7/9/f/79f9deba8256ece2bef97b0898c978b382.png)
— квантиль уровня

нецентрального распределения Стьюдента c числом степеней свободы равным

и параметром нецентральности

.
Для

,

,

,

, имеем

,
![$t_{0.9}[2, \sqrt 3 u(\sqrt [N] {0.85})] \approx 8.056133265$ $t_{0.9}[2, \sqrt 3 u(\sqrt [N] {0.85})] \approx 8.056133265$](https://dxdy-03.korotkov.co.uk/f/2/d/9/2d9caaf878a91b5d29604fae98af52a782.png)
.
Расчеты выполнены в Maple 12:
Код:
> with(Statistics):
> L:= 3: N:= 2: p:= 0.85:
> epsilon:= 0.1: # epsilon = 1 - gamma
> u:= Quantile(Normal(0, 1), p^(1/N));
u := 1.418341423
> Quantile(NonCentralStudentT(L-1, sqrt(L)*u), 1-epsilon);
8.056133265
2. Демонстрационный пример. Пусть «составной» эксперимент включает:
1. Получение выборки объемом L; вычисление по подвыборке объема L частных значений оценок m, S.
2. i) Обнуления счетчика b оценки p.
ii) Выполнение серии из Length экспериментов, каждый из которых состоит из: генерации выборки объемом  ; вычисления
; вычисления  ; и увеличения на единицу b в случае выполнения неравенства
; и увеличения на единицу b в случае выполнения неравенства  .
.
iii) По завершению серии экспериментов b/Length — оценка  — сравнивается с заданным уровнем
— сравнивается с заданным уровнем  .
.
Тогда, при достаточно большом числе повторений (Rep) составного эксперимента и достаточно большой длине Length серии экспериментов в каждом составном эксперименте, оценка gamma*=Count/Rep накрыть толерантным интервалом заданную долю p распределения будет приближенно равна заданному доверительному уровню

. Для демонстрации этого был написан простой пример в среде Delphi 5.0. Для того, чтобы не загромождать текст, «генератор» нормально распределенных случайных величин вынесен в отдельный модуль NormRND [текст этого модуля (используемого и в предыдущем демонстрационном примере) помещен в приложении к этому сообщению].
Код:
uses NormRnd;
const
p = 0.85;
gamma = 0.9;
t : Double = 8.056133265; { t_0.9 [2, sqrt(3)*u(0.85^(1/2))] = 8.056133265}
L = 3;
N = 2;
Length = 100000;
mu: Double = 1;
sigma: Double = 1;
Rep = 100000;
var
X: array[1..L+N] of Double;
m, s, xN : Double;
Count, b : LongInt;
i, j, k : LongInt;
C : Double;
begin
Count:= 0; InitN1DRnd(mu, sigma); C:= t/sqrt(L);
for j:= 1 to Rep
do begin
for i:= 1 to L do X[i]:= N1DRnd;
m:= 0; for i:= 1 to L do m:= m + X[i]; m:= m/L;
s:= 0; for i:= 1 to L do s:= s + sqr(X[i]-m); s:= sqrt(s/(L-1));
b:= 0;
for k:= 1 to Length
do begin
for i:= 1 to N do X[i]:= N1DRnd;
xN := X[1]; for i:= 2 to N do if X[i] > xN then xN:= X[i];
if xN < m + C*s then inc(b);
end;
if b/Length >= p then inc(Count);
end;
writeln('gamma* =', Count / Rep, 'Pres kay "Enter"'); readln;
end.
При Rep = Length = 100000, получено

.
3. По поводу обобщения на произвольное двухпараметрическое распределение. Описанный способ построения верхнего толерантного интервала существенно опирается на то, что случайные величины

являются независимыми и одинаково нормально распределенными. Для иных двухпараметрических распределений таким образом построить толерантный интервал нельзя.
Приложение. Исходный текст модуля используемого для генерации нормального распределения. Краткое описание и ссылка в
описании первого демонстрационного примера.
Код:
Unit NormRND;
interface
procedure InitN1DRnd(Mean, StdDev : Double);
function N1DRnd: Double;
implementation
type
TNRndParam = record
FNext: Boolean;
Next : Double
end;
TN1DRndParam= record
Mean: Double;
StdDev: Double;
end;
var
NRndParam : TNRndParam;
N1DRndParam: TN1DRndParam;
procedure InitNRnd;
begin NRndParam.FNext := False; end;
function NRnd: Double;
var
V1, V2, S, sqrtS : Double;
begin with NRndParam do begin
If Not FNext
then
begin
repeat
V1 := 2 * Random - 1; V2 := 2 * Random - 1;
S := V1 * V1 + V2 * V2
until s < 1;
sqrtS := Sqrt(-2 * Ln(S) / S);
NRnd := V1 * sqrtS; Next := V2 * sqrtS; FNext := True;
end
else
begin
NRnd := Next; FNext := False
end
end {with} end; {function}
procedure InitN1DRnd;
begin N1DRndParam.Mean := Mean; N1DRndParam.StdDev := StdDev; InitNRnd end;
function N1DRnd: Double;
begin with N1DRndParam do begin N1DRnd := Mean + StdDev * NRnd end {with} end;
end.



