У меня такое ощущение, что задача общеизвестная и решение давно существует, но что-то в голову никак не приходит формальное доказательство.
Имеется решение урчп по явной схеме(вообще Кранк-Николсон, но с явной схемой понятнее вроде), М точек по времени, N по координате

Если

- оператор явной схемы, а

- дифференциальный оператор уравнения, то если

- решение урчп, то

а
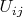
- численное решение, т.е.

как матричное уравнение.
Тогда если ввести ошибку конечных разностей на решении:

, где

взято в точках сетки, а

- реальная ошибка, то


В явном виде

:

Собственно, дальше вопрос, правильно ли следующее рассуждение и как формально доказать:
1) Если

во всех точках сетки одного знака, то

тоже одного знака(насколько я так понимаю, если доказать, что

- М-матрица, то это верно)
2) Норма

убывает при увеличении

? И как это строго доказать? Припоминается, что используется где-то жорданова форма вроде ;)
Если оба утверждения верны, то ошибка

убывает монотонно при увеличении количества точек по x, что я и наблюдаю в самом решении, но хочу обосновать теоретически.



