Докажем, что для любого
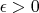
можно найти такую энку точек (по одной из каждой
последовательности решений уравнения

), что их диаметр их множества меньше

. Возьмем в качестве опорной последовательности последовательность натуральных чисел. Пусть дробь

- достаточно точное прибижение к

с погрешностью

(мы его можем сделать сколь угодно малым). Используя, например, цепные дроби, можно найти хотя бы два

отличаются от некоторого натурального числа не более чем на

, причем, используя цепные дроби,

можно сделать сколь угодно малым. Возьмем теперь k
арифметических прогрессий, у которой первые 2 члена - соответствующие два числа

, взятые по порядку, обозначим ее как

,

- знаменатели дробей

. Подставляя

мы получим k последовательностей точек

, которые отличаются от некоторых натуральных чисел не более чем на

. Теперь, если у этих последовательностей есть общий член S (общие члены образуют тоже арифметическую прогрессию), то взяв его в качестве всех

мы получим энку точек, диаметр множества которых не больше наибольшего из чисел

, где

. Ввиду того, что погрешности

можно сделать сколь угодно малыми, мы можем сделать диаметр сколь угодно малым, в том числе и меньше

. Таким образом, остается доказать существование S. Оно, например, обязательно существует при попарно взаимно простых

. Но это так не очевидно. С другой стороны, у нас есть произвол в выборе опорной последовательности.
Существование S. По индукции. База. Пусть мы взяли некоторые знаменатели

и

дробей

и

. Если

не взаимно просто с

, мы можем взять другое

, более точное, чем предыдущее

уже с другим

. Теперь опять проверяем взаимную простоту

и

. Если они опять не взаимно просты, то находим

и

и т.д. Если хотя бы один

будет, то мы его берем в качестве коэффициента для

. В противном случае мы получаем утверждение о том, что существует такое действительное число

, у которого начиная с некоторого номера знаменатели

цепных дробей не взаимно просты (какие?). Таких действительных чисел по свойству цепных дробей нет. Значит у нас уже есть

и

.
Шаг индукции. Повторяем рассуждения. Пусть есть дроби

и соответствующие взаимно простые знаменатели

. Мы таким же образом начинаем искать

. Оно должно быть взаимно просто каждому из

, что равносильно тому, что

взаимно просто

- некоторому числу. Опять же в силу свойств цепных дробей такое число

должно быть найдено.
По индукции доходим до n, получаем, что существует энка взаимно простых

, а значит S.



