Теорема Кантора: конец векового спора.

[MaximKat]

кстати, кто-то знает чем закончилась история с неназываемым и прокураторой?

[nikov]

MaximKat писал(а):

извините, но

Цитата:

все такие действительные числа, которые могут быть охарактеризованы при помощи конечных (но неограниченных в совокупности) последовательностей русских слов

это не математическое определение
слова не несут конкретного математического смысла

Это можно поправить. Возмем какую-нибудь аксиоматизацию математики, например ZFC, она использует счетный алфавит. Множество конечных строк в этом алфавите счетно. Некоторые из них (не более чем счетное множество) являются предикатами с одной свободной переменной. Некоторые из этих строк (не более чем счетное множество) являются предикатами с одной свободной переменной, которые становятся истинными только при подстановке вместо этой свободной переменной некоторого единственного объекта. Для некоторых из этих строк (не более чем для счетного множества) этот объект является действительным числом в интервале $(0; 1)$. Таким образом мы установили соответствие между натуральными числами (номерами этих строк) и некоторым подмножеством интервала действительных чисел $(0; 1)$. Теперь построим диагональное число: его $n$-ый разряд в десятичной системе равен $1$, если $n$-ый разряд $n$-го элемента нашего множества равен $2$, и равен $2$ в противном случае. Очевидно, это будет какое-то новое число из интервала $(0; 1)$. Если бы нам удалось формализовать указанное построение в ZFC, то мы бы пришли к парадоксу. Скорее всего, это построение формализовать нельзя (если мы верим в непротиворечивость ZFC и истинность доказуемых в ней теорем).

[ZVS]

[маткиб]

nikov в сообщении #174825 писал(а):

Скорее всего, это построение формализовать нельзя

И здесь доказали теорему Тарского

[MaximKat]

http://www.dpmms.cam.ac.uk/~wtg10/richardsparadox.html - вот хорошее объяснение парадокса Ришара

[shpeer]

MaximKat писал(а):

кстати, кто-то знает чем закончилась история с неназываемым и прокураторой?

На форуме МИФИ он пишет , что очередное заседание - 12 числа сего месяца

[Someone]

nilozov в сообщении #174697 писал(а):

Поэтому я предлагаю покинут теорию множеств с её аксиомами и обратить своё внимание исключительно на теорему о несчётности.

nilozov в сообщении #174716 писал(а):

А сейчас либо забываем про всю аксиоматику теории множеств и обращаемся ТОЛЬКО к теореме о несчётности множества действительных чисел и парадоксу Ришара, либо я умываю руки.

Мне, конечно, хочется назвать Вас настоящим именем, но я пока воздержусь.

Скажите, а Вы не хотите провести соревнования по сёрфингу (катанию на волнах морского прибоя) в центре Сахары? Мне кажется, это было бы легче устроить.

Вы не понимаете, что теорема Кантора и теорема о несчётности множества действительных чисел - это теоремы достаточно конкретных теорий множеств? Или Вы воображаете, что математические теоремы существуют сами по себе, вне связи с какими-либо математическими теориями? Если мы откажемся от теории множеств, то предмет обсуждения просто исчезнет.

Обращаю также внимание на то, что канторовская теория множеств сейчас может кого-либо интересовать исключительно в историческом плане, поскольку она противоречива. Поэтому обсуждать данные теоремы имеет смысл только в одной из современных стандартных теорий множеств, то есть, либо в ZFC (теория Цермело - Френкеля с аксиомой выбора), либо в чуть более сильной теории GB (теория Гёделя - Бернайса, также с аксиомой выбора).

И помните поговорку: в чужой монастырь со своим уставом не ходят.

nilozov в сообщении #174716 писал(а):

Итак, либо рассматриваем ТОЛЬКО теорему о несчётности мн.д.ч, либо я ухожу.

Если Вы не согласны, можете "умывать руки". Правда, публика лишится развлечения.

nilozov в сообщении #174716 писал(а):

Логика - наука, и ЛЮБОЙ человек, выдающий себя за учёного, ОБЯЗАН её знать. И не делайте никаких ссылок на т.н. математическую логику. Как нет филологической или исторической логики, так нет и математической.

Вы философ, что-ли? А чего Вы полезли в математику?

Нравится Вам или нет, пользоваться мы будем не философским словоблудием, именующим себя логикой и диалектикой, а классической математической логикой, или интуиционистской логикой, или, может быть, ещё какой, если понадобится, но в любом случае формально построенной, чтобы были явно видны используемые средства.

nilozov в сообщении #174768 писал(а):

Но я не буду спорить, приведу лишь точку зрения трансцендентального идеализма на аксиоматизацию геометрии - "это извращение" (А. Шопенгауэр)

Начхать на Шопенгауэра вместе с трансцендентальным идеализмом. Он в математике не разбирался.

nilozov в сообщении #174697 писал(а):

Если функция существует, то существует и предикат? А как же быть с парадоксом Ришара? Там и функция существует, и множество, но всё равно рассуждение приводит к парадоксу, Что же этот "парадокс" может отрицать? - только существование функции!

Запишите этот парадокс в формальном языке теории ZFC. Тогда будет о чём говорить. А пока формального построения нет, парадокс Ришара относится к лингвистике.

nilozov в сообщении #174768 писал(а):

Я вам формально могу доказать существованеи бога, я могу набрать от балды постулаты и вывети их них, чисто формально, любое утверждение. Что, я получу истину?

Так Вы заняты Поисками Абсолютной Истины? Тогда это не к нам. Математика этим не занимается. Математика занимается построением моделей и классификацией.

nilozov в сообщении #174728 писал(а):

две посылки - существует биекция и ДПК на ней - предикат выделения.
Противоречие отрицает последнюю посылку.

nilozov в сообщении #174564 писал(а):

противоречие отрицает последнюю посылку, КОТОРУЮ ОНО ИСПОЛЬЗОВАЛО

Вообще, такого правила нет и не может быть. Если в Вашей "логике" такое правило есть, то это не логика, а словоблудие, с помощью которого можно доказать что угодно. Демонстрирую на той же теореме Кантора. Пока оставим в стороне спор о "существовании" предиката $x\notin fx$ для сюръекций.

Итак, пусть имеется произвольное отображение $f\colon X\to 2^X$.
1) Определяем множество $Z=\{x:x\in X\&x\notin fx\}$.
2) Предположим, что существует такой элемент $z\in X$, что $fz=Z$.
Элемент $z$ либо принадлежит подмножеству $Z$, либо не принадлежит ему.
3) Предположим, что $z\in Z$.
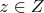
4) Тогда по определению $Z$ должно быть $z\notin Z$.
5) Поскольку это противоречит предположению 3), оно отрицается. Стало быть, $z\notin Z$.
6) Тогда, опять же по определению $Z$, будет $z\in Z$.
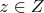
7) Поскольку 5) и 6) оба следуют из 2) и противоречат друг другу, предположение 2) отвергаем (как последнее предположение в наших рассуждениях). Стало быть, не существует такого $z\in X$, что $fz=Z$.
8) Предположим, что отображение $f$ сюръективно.
9) Тогда, по определению сюръективного отображения, существует такое $z\in X$, что $fz=Z$.
10) Поскольку 9) и 7) противоречат друг другу, отрицаем последнее использованное предположение 8). Таким образом, отображение $f$ не является сюръекцией. В частности, оно не является взаимно однозначным.
11) Этим доказано, что $|X|\neq\left|2^X\right|$.
12) Отображение $f\colon X\to 2^X$, определяемое равенством $fx=\{x\}$ для всех $x\in X$, является инъективным, поэтому $|X|\leqslant\left|2^X\right|$.
13) Из 11) и 12) следует, что $|X|<\left|2^X\right|$.

Обращаю также Ваше внимание на то, что предикат $x\notin fx$ - это не предположение. Это, как сказано в одном известном фильме, "допустимое в обществе ругательство". В математической логике то, что Вы называете предикатом, есть формула $\Phi(x)$ в языке теории, в которую переменная $x$ либо вообще не входит, либо входит свободно.

nilozov в сообщении #174520 писал(а):

вам не кажется странным то, что предикат выделения задаётся на отображении, существование которого он опровергает?

Нет, не кажется. Это означает, что предположение о существовании отображения является ложным.

nilozov в сообщении #174697 писал(а):

Я же вам много раз говорил верна лишь связка - если существет не-сюрьективная функция, то существует предикат ДПК.

Ловлю на слове.

Предположим, что $X\neq\varnothing$ (для пустого $X$ теорема Кантора проверяется непосредственно), и пусть существует сюръекция $f\colon X\to 2^X$. Возьмём любой элемент $x_1\notin X$ и положим $X_1=X\cup\{x_1\}$. Тогда $2^X\subset 2^{X_1}$. Определим отображение $f_1\colon X_1\to 2^{X_1}$ так:

$$f_1x=\begin{cases}fx\text{, если }x\in X\text{,}\\ \{x_1\}\text{, если }x=x_1\text{.}\end{cases}$$

Отображение $f_1$ не является сюръективным, так как существует элемент $x\in X$, и подмножество $\{x,x_1\}$ не является образом никакого элемента множества $X_1$. Поэтому мы имеем полное право определить множество $Z=\{x:x\in X_1\&x\notin f_1x\}$. Как и раньше, доказывается, что не существует никакого $z\in X_1$, удовлетворяющего условию $f_1z=Z$.
Заметим, что $x_1\notin Z$, так как $x_1\in f_1x_1$, поэтому $Z\subseteq X$. Таким образом, $Z\in 2^X$ и не существует никакого $z\in X$, удовлетворяющего условию $fz=Z$, что противоречит сюръективности $f$. Следовательно, предположение о существовании сюръекции неверно.

Добавлено спустя 6 минут 3 секунды:

nilozov в сообщении #174789 писал(а):

Мне жалко тратить своё время на бессмысленные препирательства.
...
Всё, ответов на форуме можете не писать.

Удрал, что ли? И ссылку на форум со своего сайта убрал...

[shpeer]

оно теперь развлекается на Коруме

[nilozov]

Вот вам обещанная логическая аргументация.

http://nilozov.narod.ru/appendix.html

За Шопенгауэра отдельное спасибо. Рассмешили.

[AD]

Краткое содержание: "математику я не знаю и знать не хочу, у меня тут своя математика, пошли все нафиг".

[nilozov]

Я имею высшее математическое образование, поэтому знаю, что говорю.

Если вам не нравиться парадокс Ришара, то возьмите парадокс Кантора.

Auf Nimmerwiedersprechen!

[AD]

nilozov в сообщении #176079 писал(а):

Я имею высшее математическое образование

Да-да, уже почти поверил.

[вздымщик Цыпа]

nilozov в сообщении #176079 писал(а):

Я имею высшее математическое образование, поэтому знаю, что говорю.

Наверно, по истории и философии математики

Цитата:

Не знаю как у читателя, но у меня не получилось апагогически продемонстрировать этот контр-тезис, поэтому я решил поменять тезис и контр-тезис местами.

Обычное дело для гуманитария. Не получается апагогически, попробуем как попало, авось вывезет.

Цитата:

Основное «возражение», которое может быть выдвинуто против моей аргументации, следующее: математики общим хором станут отрицать подчинение математики законам логики - у них, мол, есть своя, «математическая» логика, которой они только и подчиняются. Я здесь ничего не выдумываю: я действительно среди прочих «возражений» получил именно такое, причём в самой категоричной форме. Такое «возражение» — грубейшее нарушение научной субординации

Не ну все поняли. Кто возражает, тот грубо нарушает субординацию. Болтуны всегда главные, а все прочие должны прислуживать. А кто тут глаголит про «математическую» логику, тот «профан» в логике «настоящей»

Цитата:

Свою работу на этом я считаю оконченной, а себя - свободным от дальнейшей полемики

Понятное дело. Еще разок спортил воздух и удалился.

На самом деле, несмотря на обилие новых лишних слов (апагогический, тезис, контр-тезис, пропедевтика и пр.), Вы в точности пересказали то, что и было раньше. У Вас функция есть, а предиката нет. Ну и большой Вам привет в связи с этим.

Впрочем, непонятно чего Вы пыжитесь. Ну не нравится Вам теория множеств такая, как она есть, базирующаяся на ненавистной Вам математической логике. Придумайте себе другую теорию, с блэкджеком и шлюхами и «демонстрируйте» там что хотите. Можете даже постулировать эквивалентность всех множеств, прикольно получится. А Кантора и его теорему оставьте математикам и н трожьте.

[Someone]

nilozov в сообщении #176079 писал(а):

Я имею высшее математическое образование

А что такое "высшее математическое образование"?

nilozov в сообщении #176079 писал(а):

возьмите парадокс Кантора

В ZFC и в GB нет парадокса Кантора.

[PAV]

Звонилов И.В. писал(а):

Свою работу на этом я считаю оконченной, а себя - свободным от дальнейшей полемики, так как уверен, что «заблуждение в борьбе с истиной разоблачит само себя»

На этом я тему закрываю.