О принципе наименьшего действия.

[Sergey.Shu]

Приветствую всех. Пришел к вам за советом и конструктивной критикой. На протяжении многих месяцев работаю над теорией, которая, как мне кажется, приводит к весьма и весьма нетривиальным результатам.

Все проблемы современной физики сводятся, по сути, к поиску моста между миром гигантских объектов (гравитация, космология) и микромиром (элементарные частицы).  Я пришел к выводу, что, на самом деле, правило одно, просто мы видим его не полностью...

В результате длительных тестов, размышлений и расчетов я пришел к выводу , что Принцип Наименьшего Действия $\delta S = 0$, пронизывающий буквально все аспекты физического мира, возможно, не полон. Он прекрасен, но он учитывает только динамику в объёме. А как мы знаем благодаря изучению чёрных дыр и тд., фундаментальная информация о нашем мире кодируется не в объёме, а на площади его границы.

Таким образом, я предполагаю, что истинный вариационный принцип, которому следует наш мир, должен учитывать и то, и другое. Он должен быть принципом информационной эффективности. Выглядит он так:

$$ \delta \!\left(\frac{S}{\Sigma}\right) = 0 $$

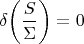
Здесь $S$ — это классическое «действие» в объёме, а $\Sigma$ — это площадь информационной границы.
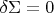
Хочу отметить, что эта минимальная поправка, с одной стороны, совершенно не ломает классической картины мира. В обычных условиях, где гравитация слаба, эффекты на границе почти постоянны ($\delta \Sigma = 0$), и мы естественным образом возвращаемся к старому доброму $\delta S = 0$. Но там, где нужны тонкие эффекты — на масштабах галактик или в мире частиц — она проявляет себя в полную силу.
Как банальный и самый тривиальный пример:
Стоит применить этот новый принцип к уравнениям Эйнштейна, как он тут же предсказывает существование фундаментального масштаба ускорения во Вселенной, который зависит только от космологической постоянной $\Lambda$ (энергии вакуума):

$$ a_\sigma = \frac{c^{2}\,\sqrt{\Lambda}}{2\pi} \;\;\approx\; 1.5 \times 10^{-10}\,\text{м/с}^2 $$

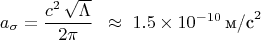
(и это прогноз теории из первых принципов, который дает такую картину)

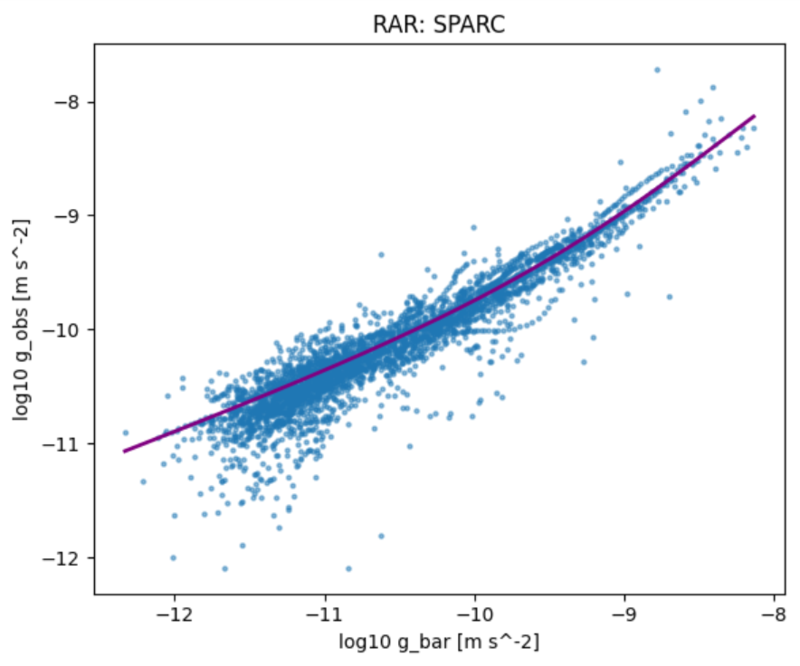
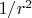
Если гравитационное ускорение от видимой материи (звёзд и газа) падает ниже этого порога, гравитация перестаёт ослабевать по закону $1/r^{2}$ и начинает спадать медленнее. Это в точности тот эффект, который мы наблюдаем во вращающихся галактиках и приписываем «тёмной материи»! Тёмная материя оказывается иллюзией, аномалией, вызванной голографической природой гравитации. Эта же формула напрямую связывает локальную динамику галактик с глобальным расширением Вселенной ($H_0$), предлагая решение знаменитого «напряжения Хаббла».

К чему я это всё?

Я не имею отношения к академическому сообществу и мне это банально не с кем обсудить. Возможно, я где-то в корне не прав и несу откровенную ерунду, но пока, исследуя вопрос в рамках своих возможностей, мне удаётся получать крайне любопытные и согласованные результаты, коих у меня накопилось уже предостаточно.

Пришел за свежим взглядом. Возможно у меня замылен глаз и я допускаю какие то фундаментальные ошибки в расчетах. Был бы признателен за любой отзыв, критику или свежее мнение. Спасибо.

[Ende]

Тема перемещена из форума «Дискуссионные темы (Ф)» в форум «Карантин»
- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы). Все формулы и даже отдельные обозначения величин латинскими или греческими буквами следует оформить правильно.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Ende]

Тема перемещена из форума «Карантин» в форум «Дискуссионные темы (Ф)»
Причина переноса: не указана.

[Утундрий]

Sergey.Shu в сообщении #1703575 писал(а):

Здесь $S$ — это классическое «действие» в объёме, а $\Sigma$ — это площадь информационной границы.

Уточните, как вычисляется $\Sigma$?

[Geen]

Sergey.Shu в сообщении #1703575 писал(а):

а $\Sigma$ — это площадь информационной границы.

Где определение этой границы?

Sergey.Shu в сообщении #1703575 писал(а):

В обычных условиях, где гравитация слаба, эффекты на границе почти постоянны

Откуда какая-то связь "гравитации" с какой-то "границей"? Что такое "гравитация" и что такое "слабая гравитация"?

Sergey.Shu в сообщении #1703575 писал(а):

применить этот новый принцип к уравнениям

Как какой-либо "принцип" можно применить хоть к каким-либо уравнениям? У них от этого решение меняется разве?

Sergey.Shu в сообщении #1703575 писал(а):

предсказывает существование фундаментального масштаба ускорения во Вселенной, который зависит только от космологической постоянной $\Lambda$

Что в нём фундаментального, и почему бы его не получить просто из анализа размерностей?

Sergey.Shu в сообщении #1703575 писал(а):

Это в точности тот эффект, который мы наблюдаем во вращающихся галактиках и приписываем «тёмной материи»!

Нет. С большой достоверностью любые модификации "гравитации" не объясняют наблюдения.

Sergey.Shu в сообщении #1703575 писал(а):

предлагая решение знаменитого «напряжения Хаббла».

Озвучьте, пожалуйста, в чём состоит это напряжение и покажите это самое решение.

И да, очень хочется увидеть применение принципа к уравнениям.

[Утундрий]

Поскольку тут такой поток требований со стороны Зарядных Устройств, то я буду настаивать на приоритете, потому как спросил первым.

[Theoristos]

Sergey.Shu в сообщении #1703575 писал(а):

$\Sigma$ — это площадь информационной границы.

Присоединюсь к вопросу, что есть "информационная граница", и как вычисляется её площадь.

Sergey.Shu в сообщении #1703575 писал(а):

та минимальная поправка, с одной стороны, совершенно не ломает классической картины мира. В обычных условиях, где гравитация слаба, эффекты на границе почти постоянны ($\delta \Sigma = 0$), и мы естественным образом возвращаемся к старому доброму $\delta S = 0$.

А у меня нет уверенности в таком утверждении. Ибо действие в той же теории поля вычисляется по некому 4-объёму, а мы делим его на некую "площадь".

Sergey.Shu в сообщении #1703575 писал(а):

Но там, где нужны тонкие эффекты — на масштабах галактик или в мире частиц — она проявляет себя в полную силу.

Тут тоже пока не пойму, как так выходит, что один и тот же вклад начинает проявлять себя и на очень больших масштабах И на очень маленьких. А в середине несущественен.

[Sergey.Shu]

Утундрий в сообщении #1703608 писал(а):

Sergey.Shu в сообщении #1703575 писал(а):

Здесь $S$ — это классическое «действие» в объёме, а $\Sigma$ — это площадь информационной границы.

Уточните, как вычисляется $\Sigma$?

Так же как...площадь. Если упростить то это площадь границы изучаемого объекта. Буквально.
Ее определение можно задать через термодинамику горизонтов:

$ \mathcal{S}=\frac{\Sigma}{4A_p},\qquad A_p=\frac{\hbar G}{c^3} $

И тогда для черной дыры это: $\(\Sigma_{\rm BH}=16\pi G^2 M^2/c^4\)$$
Для вселенной: $\(\Sigma_{\rm U}=4\pi c^2/\Lambda\)$$

Если грубо ячейки панковской площади $A_p$, по сути, играют роль ячеек памяти.

Что касается последующих вопросов - для прояснения ситуации обратимся к Эйнштейну, там и гравитация без гравитации и уравнение и разница в подходах очевидна:

Суть нового вариационного принципа:
$\[ \delta\!\left(\frac{S}{\Sigma}\right)=0 \;\;\Longleftrightarrow\;\; \delta\!\big[S-\lambda\,\Sigma\big]=0,\quad \lambda=\frac{S}{\Sigma}=\text{constant}. \]$

Стандартные уравнение Энштейна получаются из вариации действия, я модифицировал сам принцип, что равносильно добавлению дополнительного члена:
$\delta(S_{EH} + S_m - \lambda\Sigma) = 0$
а значит: $G_{\mu\nu} = 8\pi G (T_{\mu\nu} + T_{\mu\nu}^{\Sigma})$
Где $T_{\mu\nu}^{\Sigma}$ новый тензор, который не равен нулю даже если обычной материи нет, это свойства самой структуры вселенной и/или ее информационной оптимизации. Именно он и дает эффекты приписываемые темной материи эффекты.


Что касается Хаббла:
В обычной космологии
$\[ \Lambda=\frac{3\,\Omega_\Lambda\,H_0^2}{c^2}. \]$

Слабополевая константа из моей теории, фиксированная самой геометрии горизонта:


$\[ a_\sigma = \frac{c^2}{2\pi}\sqrt{\Lambda}. \]$

И тогда постоянная Хаббла выражается так:
$\[ \boxed{\,H_0^{(\mathrm)}=\frac{2\pi\,a_\sigma}{c\,\sqrt{3\Omega_\Lambda}}\,} \;\;\approx\;67.6 \;\text{км/с/Мпк}. \]$

Что почти идеально совпадает с параметрами ранней вселенной.

[Утундрий]

Яснее не стало. Продемонстрируйте на примере.

[Geen]

Sergey.Shu в сообщении #1703697 писал(а):

Для вселенной: $\(\Sigma_{\rm U}=4\pi c^2/\Lambda\)$

То есть это константа? То есть её вариация всегда равна 0? То есть никакого влияния эта площадь не оказывает? То есть возвращаемся к исходной форме "действия"?

[bb77]

Sergey.Shu в сообщении #1703697 писал(а):

И тогда для черной дыры это: $\(\Sigma_{\rm BH}=16\pi G^2 M^2/c^4\)[math]$$
Для вселенной: $\(\Sigma_{\rm U}=4\pi c^2/\Lambda\)$$[/math]

Если одно для ЧД, другое для вселенной, то как вы потом чуть ниже по тексту перескакиваете к объяснению эффектов тёмной материи?

[amon]

Sergey.Shu в сообщении #1703697 писал(а):

Суть нового вариационного принципа:
$\delta\left(\frac{S}{\Sigma}\right)=0\Longleftrightarrow\delta(S-\lambda\,\Sigma)=0$

Давайте с него и начнем.
1. Кто такие $S$ и $\Sigma,$ от каких переменных они зависят? По какой (каким) переменным производится варьирование?
2. В общем случае $\delta\left(\frac{S}{\Sigma}\right)=0\Longleftrightarrow\delta(S-\lambda\,\Sigma)=0$ неверно. Покажите как у Вас это получается.

[pppppppo_98]

я думаю на этом нужно и заканчивать обсуждение..графомания, надерганы куски из моделей ОТО, и в произвольном порядке собраны...Да кстати когда начинают произносить слово информация в любом контексте контексте, кроме как энтропия взятая с обратным знаком, это тут же вызывает подозрительные вопросы

[Sergey.Shu]

Извиняюсь за задержку с ответом, был занят хромодинамикой. Но обвинении в графомании меня порядком позабавило. Спасибо!

Теперь к сути.

Что такое $\Sigma$

$\Sigma$ — это, по сути, если упростить, фундаментальное квантово-информационное поле, лежащее в основе всей физической реальности. Прошу заметить
, я постулирую не десятки ничем не обоснованных абстрактных полей, как классическая физика ,а одно, вполне конкретное и определенное...

- Оно не «живет» в пространстве, а само является пространством в его глубинном проявлении.
- Его базовое свойство — квантование и память: каждая элементарная ячейка памяти имеет площадь
$ \[ \Delta\Sigma = 8\pi A_p, \qquad A_p = \frac{\hbar G}{c^3}, \] $
и соответствует одному кванту фазы времени
$ \[ \Delta\varphi = 2\pi. \] $
- Таким образом, $\Sigma$ — это «океан фазы», состоящий из дискретных ячеек памяти.

Частицы в этой картине — устойчивые топологические дефекты (вихри) поля Σ.
Масса — это частота, с которой фаза записывается в ячейки Σ.
Гравитация — это коллективная динамика деформаций поля Σ.

Пример простого применения $\Sigma$: фундаментальное ускорение

1. Формула
В слабом поле принцип даёт универсальное ускорение:

$\[ a_\sigma = c^2 \sqrt{\Lambda} \]$

где
- $c = 3.0\times 10^8$ м/с — скорость света,
- $\Lambda \approx 1.1 \times 10^{-52}$ м$^{-2}$ — космологическая постоянная.

---

2. Считаем
$\[ a_\sigma = (3.0\times 10^8)^2 \cdot \sqrt{1.1\times 10^{-52}} \]$

$\[ a_\sigma \approx 1.5 \times 10^{-10}\,\text{м/с}^2 \]$

---

Что это значит в жизни
- Это ускорение в 10 миллиардов раз меньше, чем земное $g = 9.8\,\text{м/с}^2$.
- Настолько крошечное ускорение вы никогда не почувствуете, но именно оно проявляется, когда смотришь на вращение звёзд в галактике: там, где по ньютоновской физике они должны бы лететь прочь, они всё ещё «держатся».



Насколько я понимаю вы просите меня применить принцип к классическим и понятным системам? Ок. Я выведу Максвелла или Эйнштейна из своей теории с минимальными правками работающими только в предельных средах. Что вам это даст? Сила теории в том что она дает предсказания и понимание именно граничных сред и так же является мостом между микро и макромиром. Поэтому призываю задавать более глубокие и фундаментальные вопросы, а не собирать пену с поверхности.

[Cos(x-pi/2)]

Бессмысленные слова - "квант фазы времени, "океан" фазы, "фундаментальное квантово-информационное поле", - да ещё и с невежественным заявлением, будто бы, мол, классическая физика постулирует "десятки ничем не обоснованных абстрактных полей", - это всё годится только для Пургатория. И нумерологией на этом форуме не надо заниматься.

Вы не ответили на главные вопросы:

amon в сообщении #1703784 писал(а):

Sergey.Shu в сообщении #1703697 писал(а):

Суть нового вариационного принципа:
$\delta\left(\frac{S}{\Sigma}\right)=0\Longleftrightarrow\delta(S-\lambda\,\Sigma)=0$

Давайте с него и начнем.
1. Кто такие $S$ и $\Sigma,$ от каких переменных они зависят? По какой (каким) переменным производится варьирование?
2. В общем случае $\delta\left(\frac{S}{\Sigma}\right)=0\Longleftrightarrow\delta(S-\lambda\,\Sigma)=0$ неверно. Покажите как у Вас это получается.

Ответьте, пожалуйста, чётко на эти два вопроса.