chislo_avogadro, Вы формулу для "смеси" не написали, поэтому непонятно, какие веса куда и как конкретно считаете зашитыми.
В коэффициенты
 веса не зашиты
веса не зашиты, и волновые функции

состояний системы, заключённой в конечный объём

считаются
нормированными на единицу, т.е. выполняются равенства:

Как члены ансамбля в статистической механике такие волновые функции и их коэффициенты

получают ещё номер

(в книге, которую изучает ТС, этот номер пишется в виде верхнего индекса), при этом указанные нормировочные равенства продолжают выполняться отдельно для каждого значения

Вот, на всякий случай, дописал до конца последний примерчик из своего предыдущего поста:
Разложения актуальных в этом примерчике двух волновых функций по в. ф. стационарных состояний (конечно же тривиальные, так как пример умышленно взял очень простой) имеют вид:


Пусть оказалось, что атом в многократных измерениях какой-то физ. величины

дал

раз результат

свойственный состоянию

причём результат

свойственный состоянию

получился

раз, и полное число измерений было

Подчеркну ещё раз: в определении матрицы плотности

индекс

нумерует все результаты измерения в ансамбле, а не только
различающиеся результаты,

Поэтому величина, обозначенная там как

в данном примерчике принимает

раз значение

и принимает

раз значение

то есть:

где

и

-- эти величины можно интерпретировать как найденные в данной экспериментальной реализации ансамбля оценки вероятности:
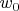
- обнаружить атом в состоянии


- обнаружить атом в состоянии

Для

в этом примерчике получается:

Это был рассказ экспериментатора, т.е. - "как экспериментатор может подобраться к теоретическим понятиям посредством вспомогательных соображений". Здесь есть нюансы: например, понятно, что если повторять снова по

штук таких же опытов, то повторные реализации одной и той же постановки опыта не обязаны точно воспроизводить друг друга - в этих других реализациях ансамбля с конечным

могут получаться какие-то немножко другие экспериментальные значения


и

(Об этом выше напомнил
pppppppo_98.)
В окончательной формулировке теории полагают

и считают, что в таком пределе величины типа

и

стремятся к определённым значениям, зависящим от заданной физики в постановке опыта, но не от "номера реализации" самого бесконечного ансамбля при одной и той же постановке опыта.
В частности, для канонического ансамбля (физика при этом такая: система с заданным числом частиц в заданном объёме, с энергетическим спектром

пребывает в равновесии с термостатом при температуре

теория предсказывает вероятности

Здесь

- мультииндекс, т.е. совокупность всех квантовых чисел, определяющих стационарное состояние

системы. Суммирование в

идёт по всем значениям квантовых чисел, а не по различным значениям энергии только; т.е. каждое значение

входит в сумму столько раз, какова кратность вырождения данного значения

Соответственно,

здесь это вероятность обнаружить систему в состоянии с данным

Вероятность же обнаружить систему с данным значением энергии

получается умножением

на кратность вырождения

этого уровня энергии




