1 12.051
2 14.557
3 17.535
4 21.303
5 29.384 2.438
6 35.535 2.441
7 42.802 2.441
8 51.878 2.435 *
9 71.627 2.438
10 86.755 2.441
11 104.498 2.441
12 126.443 2.437 *
13 174.509 2.436 *
14 211.810 2.441
15 255.145 2.442
16 308.347 2.439
17 424.769 2.434 *
18 517.118 2.441
19 623.010 2.442
20 752.215 2.440
21 1032.114 2.430 *
22 1262.451 2.441
23 1521.316 2.442
24 1835.511 2.440
25 2497.414 2.420 *
26 3081.836 2.441
27 3714.963 2.442
28 4479.769 2.441
29 5669.383 2.270 *
30 7522.496 2.441
31 9071.840 2.442
32 10934.970 2.441
33 13469.518 2.376 *
34 18359.340 2.441
35 22153.280 2.442
36 26695.000 2.441
37 32624.810 2.422 *
38 44799.710 2.440
39 54097.660 2.442
40 65174.480 2.441
41 79305.190 2.431 *
42 109292.050 2.440
43 132103.100 2.442
44 159131.670 2.442
45 193087.970 2.435 *
46 266536.230 2.439
47 322580.200 2.442
48 388561.000 2.442
49 470547.210 2.437 *
50 649700.130 2.438
51 787677.400 2.442
52 948811.600 2.442
53 1147363.000 2.438 *
54 1582506.900 2.436 *
55 1923269.500 2.442
56 2316939.000 2.442
57 2798774.900 2.439
58 3849742.400 2.433 *
59 4695774.300 2.442
60 5657949.900 2.442
61 6828988.200 2.440
62 9341737.300 2.427 *
63 11464168.200 2.441
64 13816887.100 2.442
65 16666113.300 2.440
66 22496451.500 2.408 *
67 27985767.900 2.441
68 33741527.000 2.442
69 40679934.000 2.441
70 50530417.300 2.246 *
71 68309261.000 2.441
72 82398565.000 2.442
73 99306715.300 2.441
74 121805140.000 2.411 *
75 166707020.000 2.440
76 201220370.000 2.442
77 242447670.000 2.441
78 295643000.000 2.427 *
79 406759870.000 2.440
80 491381190.000 2.442
81 591956360.000 2.442
82 719289910.000 2.433 *
83 992201840.000 2.439



 по формуле Римана.
по формуле Римана. , как раз выбираю оптимальное число нулей.
, как раз выбираю оптимальное число нулей. в лоб, то есть строго по формуле Римана. Владеете Вы этим усовершенствованным методом?
в лоб, то есть строго по формуле Римана. Владеете Вы этим усовершенствованным методом? использовать метод Платта?
использовать метод Платта?
 при этом
при этом 
 подразумевается вовсе не primepi(x), а выражение primepi(x)-if(frac(x)==0&&isprime(x),0.5,0).
подразумевается вовсе не primepi(x), а выражение primepi(x)-if(frac(x)==0&&isprime(x),0.5,0). . Потому что
. Потому что  !
! . Правда, значения не полностью совпадают.
. Правда, значения не полностью совпадают.
 потому что дзета-столбец примерно равен
потому что дзета-столбец примерно равен 


 раза.
раза.
 и до
и до  показаны ниже. Также показаны соотношения между этими точками. Значение
показаны ниже. Также показаны соотношения между этими точками. Значение  . Видно что эти аномалии периодически передают эстафету — в этих местах звёздочки стоят вплотную.
. Видно что эти аномалии периодически передают эстафету — в этих местах звёздочки стоят вплотную. даёт очень хорошие приближения к
даёт очень хорошие приближения к  и
и  .
. и
и  , а также и в других точках из таблицы выше. Потому что два самых главных нуля никакого вклада не дают, а остальные нули вряд ли дадут большую сумму и сильную аномалию.
, а также и в других точках из таблицы выше. Потому что два самых главных нуля никакого вклада не дают, а остальные нули вряд ли дадут большую сумму и сильную аномалию.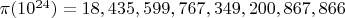 ?
? :
: .
.