n=155921
1: 14389.0370810906 17.0674522471 -0.6931471806 0.0000000000 = 14405.4113861571
2: -42.2802358371 0.0997350812 0.3465735903 -0.0000002488 = -41.8339274144
3: -6.4789166691 -0.1243403752 0.2310490602 -0.0000129638 = -6.3722209479
5: -1.3122730261 0.1072749823 0.1386294361 -0.0002978887 = -1.0666664964
6: 0.8213114166 0.0435656436 -0.1155245301 0.0006474669 = 0.7499999970
7: -0.5638964859 -0.0339993911 0.0990210258 -0.0011250378 = -0.4999998891
10: 0.2430228397 0.0232568337 -0.0693147181 0.0030351361 = 0.2000000914
11: -0.1938109652 0.0436362423 0.0630133801 -0.0037480044 = -0.0909093473
13: -0.1289850667 0.0039348721 0.0533190139 -0.0051919374 = -0.0769231181
14: 0.1069241061 0.0081097929 -0.0495105129 0.0059051828 = 0.0714285689
15: 0.0892958839 0.0169753052 -0.0462098120 0.0066051261 = 0.0666665032
17: -0.0632096301 -0.0284337889 0.0407733636 -0.0079529708 = -0.0588230262
14389.037081090565938281780070180898713\\li(n)
14356.500011078238148023773800925770675
14357\\pi(n)



![$\frac{\mu(k)}{k}J(\sqrt[k]{n})$ $\frac{\mu(k)}{k}J(\sqrt[k]{n})$](https://dxdy-02.korotkov.co.uk/f/d/5/f/d5ffd4115cc4a524748d1bb4a268a29782.png) , где
, где  это номер строки (левая колонка), в колонках все 4 слагаемых
это номер строки (левая колонка), в колонках все 4 слагаемых  и в самой правой итог суммирования. Всё строго по книге Дербишира "простая одержимость", глава 21, таблица 21.1, стр. 409.
и в самой правой итог суммирования. Всё строго по книге Дербишира "простая одержимость", глава 21, таблица 21.1, стр. 409. .
. , а тоже доопределённые до дробных значений на простых.
, а тоже доопределённые до дробных значений на простых. беру не целое, а с прибавкой
беру не целое, а с прибавкой 
 - так задана
- так задана  :
:

 , так что в них не чистая
, так что в них не чистая  .
. , то
, то  , где
, где  - указанная верхняя граница.
- указанная верхняя граница. . (1)
. (1)  и сравнивают изменение суммы нетривиальных нулей при увеличении
и сравнивают изменение суммы нетривиальных нулей при увеличении  (требуемая точность).
(требуемая точность). . Тогда требуемое количество нулей определяется с использованием формулы (1) -
. Тогда требуемое количество нулей определяется с использованием формулы (1) - 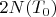 .
. Платт использовал 69.7 млрд нулей.
Платт использовал 69.7 млрд нулей. рекомендуют начинать с
рекомендуют начинать с  пока не достигается требуемая точность -
пока не достигается требуемая точность -  .
. так потребуются нули до
так потребуются нули до  , которых будет порядка
, которых будет порядка  штук!! Хотя люди сумели обойтись всего лишь 103 миллиардами.
штук!! Хотя люди сумели обойтись всего лишь 103 миллиардами.