маткиб писал(а):
как определить истинность этой формулы? Этот вопрос уже точно относится к математике.
А вот и нет

Не согласен.
Это вопрос только нашего собственного решения: принимаем мы теорию (доказывающую эту формулу) или нет. Если теория принята (т.е. мы
верим, что она состоятельна), то всякое доказанное в ней утверждение "истинно" (с нашей точки зрения). Поэтому я всегда подчёркивал: я не понимаю что такое "истинность вне теорий". Вот Вы принимаете аксиому бесконечности, а я - нет. Стало быть Ваше представление об "истинности" утверждения о существовании счётной бесконечности иное, чем моё.
маткиб писал(а):
Для того, чтобы упростить процесс определения истинности, математик может придумать формальную теорию, которая, по мнению математика, позволяет доказывать только истинные формулы.
В том-то и дело, что
любая формальная теория, коль уж она
принята нами, "позволяет доказывать только истинные (с нашей точки зрения) формулы" - просто по определению. А "процесс определения истинности" - это ни что иное, как процесс доказательства в рамках принятой теории. Как только Вы усомнились в том, что доказанное => истинное, теория сразу же перестаёт быть "принятой".
маткиб писал(а):
Но вопрос о придумывании таких теорий тоже относится к математике (а к чему же ещё?).
А вот ни к чему он не должен относиться. Точнее, вопрос придумывания формальной теории - это, конечно же, математика. Но вот вопрос о том, доказывает ли она "только истинные формулы", это вовсе не "вопрос", а, как Вы правильно выразились, это всего лишь "мнение" (причём мнение не обязательно самого математика, а и пользователей его теории в том числе).
маткиб писал(а):
Если, например, ZFC не позволяет ответить на вопрос, который эквивалентен существованию нужной ракеты, то нужно придумать что-то такое, что позволит ответить на этот вопрос. И заявления о неразрешимости тут недопустимы.
Разумеется нужно придумать формальную теорию, которая бы отвечала на вопрос, раз уж он стоит на практике. И ZFC тут не причём, эта теория может не иметь к ней никакого отношения.
маткиб писал(а):
Более того, никаких принципиальных неразрешимостей не известно, поэтому не исключено, что с помощью мышления можно установить истинность любого корректного утверждения.
Я не знаю, что Вы называете "принципиальной" неразрешимостью. С моей точки зрения неразрешимость

в

это:

Разумеется, это утверждение тоже сформулировано в рамках некой теории (каковая по отношению к

является мета-теорией, ибо может формулировать утверждения касательно того, являются ли те или иные высказывания в синтаксисе

её теоремами). И разумеется, что можно придумать расширение

, в котором

будет так или иначе разрешимо.
маткиб писал(а):
Не уловил Вашу мысль. Мы говорили только о доказуемости или недоказуемости в ZFC. С моей точки зрения ZFC здесь не то что бы предел, а даже вовсе избыточна. Можно было бы говорить о доказуемости или недоказуемости в арифметике.
Говорить можно, но арифметика (Пеано) может и не ответить на вопрос о доказуемости. А ZFC, например, может. И какой вывод из этого делать? Или ZFC не может, а какая-нибудь более сильная теория может. Что делать в таких случаях?
ZFC тут не причём, в ней куча совершенно лишнего и бесполезного с точки зрения решения вопроса разрешимости тех или иных арифметических выражений. Я ведь выше говорил о чём? Допустим, есть некое арифметическое выражение

и мы исследуем вопрос его доказуемости в арифметике Пеано

, т.е мы хотим знать: верно ли

. Обозначим ту теорию, в которой мы пытаемся доказать это высказывание, как

(мета-арифметика). Бьёмся, бьёмся - ни доказать, ни опровергнуть не можем. Тогда мы "поднимаемся на ступеньку выше" и пытаемся рассмотреть вопрос доказуемости уже в

, т.е. начинаем рассуждать в рамках "мета-мета-арифметики"

. И вот, "успех" - в рамках

нам удаётся совершенно строго доказать, что:

Т.е. то, о чём я говорил выше: вопрос о доказуемости в арифметике
 неразрешим
неразрешим (в мета-арифметике), и это доказано (в мета-мета-арифметике). Воможна такая ситуация? Я полагаю что да, причём

и

могут не использовать
ни одной дополнительной аксиомы по отношению к

.
маткиб писал(а):
Поэтому Ваше высказывание о том, что "доказательство либо существует, либо нет" представляется мне некорректным.
Совершенно не понимаю, почему оно Вам представляется некорректным.
Вот это высказывание :

Я понимаю, что это не то же самое, что:
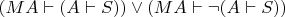
Но одно весьма близко к другому

Второе прямо противоречит тому случаю, который я описал выше. Первое - не противоречит. Но прийти к первому, не имея второго, мы можем
только если искусственно воткнём в теорию  закон исключённого третьего
закон исключённого третьего. А это с моей точки зрения и есть некорректность - использовать закон исключённого третьего только для того, чтобы доказывались подобные утверждения (а я не знаю для чего ещё он может быть использован).



