В том же параграфе (§13, гл. III) в пункте 2 определяются эмпирическая функция распределения

и величина

(

- последовательность н.о.р. случайных величин,

).
В пункте 3 доказывается, что если

непрерывна, то
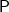
-п.н.
![$$D_N(\omega) = \sup_{y\in [0,1]} |U_N(y;\omega)-y|,$$ $$D_N(\omega) = \sup_{y\in [0,1]} |U_N(y;\omega)-y|,$$](https://dxdy-02.korotkov.co.uk/f/d/4/a/d4aa55b61c80d61f7876714f0f462b5a82.png)
где

- эмпирическая функция распределения н.о.р. случайных величин

, имеющих равномерное (U=U(y)) распределение на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. А в пункте 4 величина

записывается уже так:
![$$D_N(\omega) = \max_{y\in [0,1]} |U_N(y;\omega)-y|.\eqno{(10)}$$ $$D_N(\omega) = \max_{y\in [0,1]} |U_N(y;\omega)-y|.\eqno{(10)}$$](https://dxdy-02.korotkov.co.uk/f/9/6/1/9612f59d12ff8a81df5a20418f28d41a82.png)
Вопросы:
1) Почему вдруг максимум вместо супремума? Ведь функция

имеет разрывы.
2) В учебнике утверждается, что

где

- порядковые статистики, т.е.

и т.д. по возрастающей. Разве не

(в точке скачка функция

)?



