Гауссовские случайные величины

[ihq.pl]

Пусть $\xi = \{\xi_1,...,\xi_n\}$ - гауссовский случайный вектор; компоненты $\xi$ линейно независимы и $\mathsf{E}\xi = (0,...,0)$. Пусть $\varepsilon_1,..., \varepsilon_n$ - ортонормированная система случайных величин, полученных из $\xi$ методом ортогонализации Грама-Шмидтa. Согласно этому методу $(\varepsilon_1,...,\varepsilon_n)\sim \mathcal{N}(0,E)$, где $E$ - единичная матрица;

$$\xi_k = \hat\xi_k + b_k\varepsilon_k,\qquad (0)$$

$$\hat\xi_k = \sum_{j=1}^{k-1}(\xi_k,\varepsilon_k)\varepsilon_k,\qquad (1)$$

$b_k = \|\xi_k - \hat\xi_k\|$, и линейные оболочки

$$\mathcal{L}(\xi_1,..,\xi_k) = \mathcal{L}(\varepsilon_1,..,\varepsilon_k)\qquad (2)$$

для любого $1\leqslant k\leqslant n$. Тогда в силу (1) и (2)

$$\hat\xi_k = \mathsf{E}(\xi_k|\xi_{k-1},...,\xi_1). \qquad (3)$$

-------------------------------------------

Возможно, что-то упускаю, т.к. у меня (3) выполняется почти наверное: в силу (0)

$$\mathsf{E}(\xi_k|\mathcal{F}_k) = \mathsf{E}(\hat\xi_k|\mathcal{F}) + b_k\mathsf{E}(\varepsilon_k|\mathcal{F}_k),\quad \text{(п.н.)}$$

где $\mathcal{F}_k$ - $\sigma$-алгебра, порожденная случайными величинами $\xi_1,...,\xi_{k-1}$. Случайная величина $\hat\xi_k$ является $\mathcal{F}$-измеримой, а $\varepsilon_k$ - независимая от $\mathcal{F}_k$. Поэтому

$$\mathsf{E}(\hat\xi_k|\mathcal{F}_k) = \hat\xi_k\quad \text{(п.н)}$$

и

$$\mathsf{E}(\varepsilon_k|\mathcal{F}_k) = 0 \quad \text{(п.н)}$$

т.к $\mathsf{E}\varepsilon_k = 0$.

Можно еще найти выражение для $\mathsf{E}(\xi_k|\mathcal{F}_k)$, используя формулу, похожую на эту

$$E(\xi|\eta=y) = \int_R xf_{\xi|\eta}(x|y)dx,$$

но это сложно. Может, есть более простые способы убедиться в том, что равенство (3) выполняется точно?

[mihaild]

ihq.pl в сообщении #1679307 писал(а):

Может, есть более простые способы убедиться в том, что равенство (3) выполняется точно?

Как это могло бы быть, если правая часть определена только с точностью до почти наверное?
Если $\xi$ - условное ожидание $\mathbb E(\eta | A)$, $\xi'$ тоже измерима относительно $A$, и $\xi = \xi'$ почти наверное, то $\xi'$ - тоже условное ожидание $\mathbb E(\eta | A)$.

[ihq.pl]

mihaild в сообщении #1679324 писал(а):

Как это могло бы быть, если правая часть определена только с точностью до почти наверное?
Если $\xi$ - условное ожидание $\mathbb E(\eta | A)$, $\xi'$ тоже измерима относительно $A$, и $\xi = \xi'$ почти наверное, то $\xi'$ - тоже условное ожидание $\mathbb E(\eta | A)$.

Не знаю, может, имеется в виду версия условного матожидания, которая получается по формуле

$$\mathsf{E}(\xi_k|\xi_{k-1}=x_{k-1},...,\xi_1=x_1) = \int\limits_{-\infty}^\infty x_k g(x_k;x_{k-1},...,x_1)dx_k,$$

$$g(x_k;x_{k-1},...,x_1) = \frac{f_{\xi_1,...,\xi_k}(x_1,...,x_k)}{f_{\xi_1,...,\xi_{k-1}}(x_1,...,x_{k-1})},$$

где $f_{\xi_1,...,\xi_k}$ - плотность распределения вектора $(\xi_1,...,\xi_k)$? В учебнике про это ни слова.

[mihaild]

Плотность тоже определена только почти всюду.

[ihq.pl]

mihaild в сообщении #1679336 писал(а):

Плотность тоже определена только почти всюду.

И гауссовская тоже? Знаменатель в функции $g$ нигде не ноль. Или я что-то не понимаю.

[mihaild]

Так, пардон, я невнимательно прочитал.

ihq.pl в сообщении #1679334 писал(а):

$$\mathsf{E}(\xi_k|\xi_{k-1}=x_{k-1},...,\xi_1=x_1) = \int\limits_{-\infty}^\infty x_k g(x_k;x_{k-1},...,x_1)dx_k,$$

Эта формула вообще не задает случайную величину. Соответственно тут вопрос - что такое $\hat \xi_k$.

А что, собственно, Вам не нравится в том, что (3) выполняется только п.н.?

[ihq.pl]

mihaild в сообщении #1679339 писал(а):

А что, собственно, Вам не нравится в том, что (3) выполняется только п.н.?

Смущает, что в учебнике (Ширяев, Вероятность-I) точное равенство. Вряд ли забыли.

mihaild в сообщении #1679339 писал(а):

Эта формула вообще не задает случайную величину.

Почему? Это - "экстраполяция" на многомерный случай формулы

$$\mathsf{E}(\xi|\eta=y) = \int\limits_R xf_{\xi|\eta}(x|y)dx,$$

где

$$f_{\xi|\eta}(x|y) = \frac{f_{\xi,\eta}(x,y)}{f_\eta(y)}.$$

[mihaild]

ihq.pl в сообщении #1679341 писал(а):

Мне не нравится, что в учебнике (Ширяев, Вероятность-I) точное равенство

В каком параграфе?

ihq.pl в сообщении #1679341 писал(а):

Это - "экстраполяция" на многомерный случай формулы

$$\mathsf{E}(\xi|\eta=y) = \int\limits_R xf_{\xi|\eta}(x|y)dx,$$

И эта формула тоже не задает случайную величину. Эта формула задает функцию $\mathbb R \to \mathbb R$, а случайная величина - функция $\Omega \to \mathbb R$.

[ihq.pl]

mihaild в сообщении #1679342 писал(а):

В каком параграфе?

Параграф 13 (Гауссовские системы), п. 4, формула (17).

-- 20.03.2025, 22:32 --

mihaild в сообщении #1679342 писал(а):

И эта формула тоже не задает случайную величину. Эта формула задает функцию $\mathbb R \to \mathbb R$, а случайная величина - функция $\Omega \to \mathbb R$.

А, ну да. Но её вроде надо понимать как $\mathsf{E}(\xi|\eta)$.

[mihaild]

ihq.pl в сообщении #1679343 писал(а):

Параграф 13 (Гауссовские системы), п. 4, формула (17)

Да, там равенство почти наверное.

[ihq.pl]

Забыли всё-таки. Или надо считать как само собой разумеющееся. Спасибо!

[mihaild]

ihq.pl в сообщении #1679343 писал(а):

Но её вроде надо понимать как $\mathsf{E}(\xi|\eta)$.

А вот так, кстати, не получится. Потому что мы задали среднее по множеству нулевой меры, интуитивно понятным способом. А вот сконструировать из этого непонятного среднего настояющую случайную величину - задача гораздо более сложная.

[ihq.pl]

mihaild в сообщении #1679477 писал(а):

мы задали среднее по множеству нулевой меры

Ну, не просто же среднее, а производная Радона - Никодима...

У Ширяева и здесь

$$\mathsf{E}(\xi|\eta=y) = \int\limits_R x f_{\xi|\eta}(x|y) dx$$

точное равенство (параграф 7, пункт 6, формула (20)). Но по идее должно быть почти наверное: для каждого $B\in\mathcal{B}(R)$

$$\int\limits_B \mathsf{E}(\xi|\eta=y)P_\eta(dy) = \int\limits_{\eta\in B}\xi d\mathsf{P} = \int\limits_{\{\eta\in B\}\cap\{\xi\in\Omega\}}\xi d\mathsf{P} = \int\limits_B\Bigl[\int\limits_R x f_{\xi|\eta}(x|y) dx\Bigr] P_\eta(dy)$$

Почему?

[Combat Zone]

Смотрите. В процессе ортогонализации Грама-Шмидта подразумевается, что случайные величины каким-то образом удалось организовать в евклидово пространство и ввести на нем скалярное произведение. Если вы вернетесь немного назад и обратите внимание на нюансы, элементами этого пространства являются не сами случайные величины, а классы эквивалентности, каждый из которых состоит из с.в. отличающихся друг от друга с нулевой вероятностью (т.е. совпадающих почти наверное). Именно на нем вводится соотв. скалярное произведение, а затем порожденную им норму, которые делают его привычным пространством $L^2$ (элементами которого являются классы эквивалентности).

Так что опечатки нет, никто ничего не забыл. Когда записывают равенство между элементами пространства $L^2$, в качестве обозначения класса берется с.в.- какой-то представитель этого класса, а дописывать слова про почти наверное становится избыточным.

[ihq.pl]

Combat Zone, спасибо!

Еще такой вопрос. Если $\xi,\eta$ - случайные величины, одна из которых, пусть $\eta$, наблюдаемая, то критерием оптимальности оценки $f(\eta)$ случайной величины $\xi$ по $\eta$ является среднеквадратичное отклонение $\mathsf{E}(\xi-f(\eta))^2$. А что является критерием оптимальности, если $\xi, \eta$ - случайные векторы из $\mathbb{R}^n$ и $\mathbb{R}^m$ соответственно?

У Ширяева оптимальной оценкой является условное матожидание $\mathsf{E}(\xi|\eta)$, как я понял, просто потому, что $\mathsf{E}(\xi_j|\eta)$ - оптимальная оценка координаты $\xi_j$ по $\eta$. В учебнике без лишних слов просто приводится теорема: Выражение для оптимальной оценки $\mathsf{E}(\xi|\eta)$ такое-то, а выражение для матрицы ошибок $\mathsf{E}[(\xi-\mathsf{E}(\xi|\eta))(\xi-\mathsf{E}(\xi|\eta))^*]$ такое-то.

Но кроме диагональных элементов в матрице ошибок есть еще недиагональные. Как быть с ними? Я попробовал так всё себе объяснить. Допустим, вектор ошибок $\xi-\varphi(\eta)$ является гауссовским с нулевым средним. Тогда характеристической функцией его распределения является функция

$$e^{-\frac{1}{2}(K t, t)},$$

где $K$ - матрица ошибок. Оптимальной естественно считать ошибку, плотность распределения которой является функцией наибыстрейшего убывания. Тогда характеристическая функция оптимальной ошибки, наоборот, должна быть функцией самого медленного убывания. Это достигается при

$$K^* = \arg\min\limits_K{(Kt,t)}$$

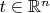
для любого $t\in\mathbb{R}^n$.