В данной теме планируется рассмотреть
модельный пример социологического(их) исследования(й) и методы верификации следствий(гипотез) из этого(их) исследования(й) .
Насколько я понимаю, типичное исследование, описанное в примере, выглядит так:
Есть некая популяция

(генеральная совокупность) с некоторым распределением

интересующей нас величины

(в модельном примере это отношение к лгбт). Мы не можем опросить всё население, чтобы получить

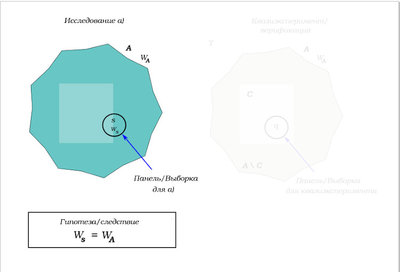
. Поэтому, чтобы получить с хорошей достоверностью картину этого распределения, мы делаем достаточно широкую репрезентативную выборку/панель

, изучаем распределение на ней

и переносим этот результат на

, то есть, считаем, что

. Это и есть результат исследования, как это следует из модельного примера
См. картинку:
Вложение:
 f.jpg [ 29.67 Кб | Просмотров: 0 ]
f.jpg [ 29.67 Кб | Просмотров: 0 ]
Далее, пусть через время

нам понадобилось по каким-то соображениям подтвердить, что (
во время исследования а)) распределение величины

по генеральной совокупности

было действительно равно именно

а не чему-то другому. Так как со временем взгляды людей могут меняться, то повторять без модификации то же самое исследование в текущее время бессмысленно -- оно покажет совсем другое. Если я правильно понимаю описание процедуры данное ув.
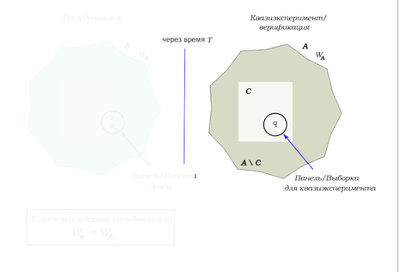
Ghost_of_past , то из всей популяции

выделяется подмножество особей

, про которых известно, что их отношение к лгбт не изменилось статистически значимо. Из

делается выборка/панель

по параметрам эквивалентная той панели, которая использовалась для исследования а). То есть величины всех переменных (таких как пол/возраст/образование/доход и тд) равны или близки. Предполагается, что

достаточно большое, чтобы делать разумное количество таких выборок.
(описание процедуры данное ув. Ghost_of_past)
Если опрос проводился по панели (а лонгитюдные опросы - самые качественные), то у нас есть возможность определить значения других независимых переменных в панели на момент проведения опроса по свойствам выборки - например, в панели опрашивалось 1200 человек с определенным половым/гендерным составом, возрастным составом, образовательным составом, географическим составом и т.д. В квазиэкспериментальном воспроизведении мы возьмем выборку с большинством сходных характеристик по этим переменным, репрезентативным стране в целом, но опросим какую-то группу, где нет статистического значимого изменения - например, представителей какого-то социального класса или жителей каких-то конкретных типов населенных пунктов/штатов и т.д., сохраняя репрезентацию распределения значений других переменных изначальной выборке.
Далее проделывается такая же работа над

, находится

и сравнивается с

.
См. картинку:
Вложение:
 e.jpg [ 25.09 Кб | Просмотров: 0 ]
e.jpg [ 25.09 Кб | Просмотров: 0 ]
Пока на этом останавливаюсь, чтобы убедиться, что я я двигаюсь в верном направлении.
Прошу
Ghost_of_past поправить меня если это необходимо.



