Вероятностная теория чисел

[vicvolf]

Была опубликована интересная статья на русском "Эффективные версии теоремы Эрдёша Винтнера" Ж. Тененбома , Ж. Вервеа по данной теме https://www.researchgate.net/publicatio ... ber_Theory

Сделаю небольшой обзор этой статьи.

Статья **"Эффективные версии теоремы Эрдёша–Винтнера"** (авторы: Ж. Тененбаум и Ж. Верве) посвящена изучению предельных распределений вещественных аддитивных арифметических функций. Основное внимание уделяется получению **эффективных оценок** для остаточных членов в теореме Эрдёша–Винтнера, а также исследованию скорости сходимости к нормальному распределению.

### Основные моменты статьи:

1. **Теорема Эрдёша–Винтнера**:
- Классическая теорема Эрдёша–Винтнера даёт критерий существования предельного распределения для вещественной аддитивной арифметической функции $ f(n) $. Условия теоремы включают сходимость рядов:
$ \sum_{p} \frac{\min(1, f(p)^2)}{p} < \infty \quad \text{и} \quad \sum_{p, |f(p)| \leq 1} \frac{f(p)}{p} \text{ сходится}$.

- Предельное распределение может быть дискретным, непрерывным сингулярным или абсолютно непрерывным.

2. **Эффективные оценки**:
- Основная цель статьи — получение **эффективных оценок** для равномерной нормы разности между эмпирической функцией распределения $F_x(y) $ и предельной функцией распределения $ F(y) $:
$ \|F_x - F\|_\infty := \sup_{y \in \mathbb{R}} |F_x(y) - F(y)|$.

- В статье доказаны две теоремы:
- **Теорема 1.1**: Для случая, когда предельное распределение дискретно.
- **Теорема 1.2**: Для случая, когда предельное распределение непрерывно.

3. **Скорость сходимости**:
- В статье явно рассматривается **скорость сходимости** к нормальному распределению. Например, в **Теореме 1.2** даётся оценка:
$ \|F_x - F\|_\infty \ll Q_F\left(\frac{1}{T}\right) + \varepsilon_x^{1/6} \log(T B_f(R) \varepsilon_x) + \eta_f(R)$,

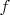
где $ Q_F $ — функция концентрации, $ \varepsilon_x $ и $ \eta_f $ — параметры, зависящие от функции $ f $ и $x $.
- В **Теореме 1.3** рассматривается случай условного распределения, где также даются оценки скорости сходимости.

4. **Примеры**:
- В статье приведены примеры, иллюстрирующие полученные результаты. Например, для функции $ f(p) = \frac{1}{(\log p)^\xi} $ показано, что скорость сходимости зависит от параметра $ \xi $.

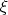
5. **Методы**:
- Основной метод доказательства — применение **теоремы 2.1** (из предыдущей работы Тененбаума), которая даёт эффективные оценки для средних значений комплексных мультипликативных функций.
- Также используются методы теории вероятностей, включая неравенство Берри–Эссеена для оценки скорости сходимости.

### Выводы:
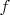
- В статье **говорится о скорости сходимости** к предельному распределению. Авторы получают явные оценки для остаточных членов, которые зависят от параметров функции $ f $ и $ x $.
- Результаты статьи позволяют лучше понять, как быстро эмпирическое распределение $ F_x(y) $ сходится к предельному распределению $ F(y) $ в зависимости от свойств аддитивной функции $ f $.

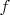
В статье "Эффективные версии теоремы Эрдёша–Винтнера" явно не формулируются условия, при которых предельное распределение аддитивной арифметической функции $f(n)$ является нормальным.

Вот еще небольшой обзор работ на данную тему:

### 1. **[2] De la Bretèche R., Tenenbaum G. "Sur la concentration de certaines fonctions additives" (2012)**:
- **Основная тема**: В этой работе изучается **концентрация распределений** аддитивных арифметических функций. Авторы исследуют, как значения аддитивных функций группируются вокруг своего среднего значения.
- **Ключевые результаты**:
- Получены оценки для функции концентрации $ Q_F(\varepsilon) $, которая измеряет, насколько вероятно отклонение значений функции от среднего на величину $ \varepsilon $.
- Показано, что для некоторых классов аддитивных функций концентрация распределения близка к нормальной.
- **Связь с нормальным распределением**: Работа предоставляет инструменты для анализа близости распределения к нормальному, хотя прямое утверждение о нормальности не формулируется.

### 2. **[6] Erdős P., Kátai I. "On the concentration of distribution of additive functions" (1979)**:
- **Основная тема**: В этой статье исследуется **концентрация распределений** аддитивных функций. Авторы изучают, как значения аддитивных функций группируются вокруг своего среднего значения.
- **Ключевые результаты**:
- Получены оценки для функции концентрации $ Q_F(\varepsilon) $.
- Показано, что для широкого класса аддитивных функций распределение значений близко к нормальному.
- **Связь с нормальным распределением**: Работа подчёркивает, что для многих аддитивных функций предельное распределение близко к нормальному, особенно если функция удовлетворяет определённым условиям на простых числах.

### 3. **[9] Koukoulopoulos D. "On the concentration of certain additive functions" (2014)**:
- **Основная тема**: В этой работе изучается **концентрация распределений** аддитивных функций. Автор рассматривает функции, которые принимают малые значения на простых числах.
- **Ключевые результаты**:
- Получены точные оценки для функции концентрации $ Q_F(\varepsilon) $.
- Показано, что для функций, которые медленно растут на простых числах, распределение значений близко к нормальному.
- **Связь с нормальным распределением**: Работа явно связывает концентрацию распределения с нормальным законом для функций, которые удовлетворяют условиям теоремы Эрдёша–Каца.

### 4. **[11] Ruzsa I.Z. "On the concentration of additive functions" (1980)**:
- **Основная тема**: В этой статье исследуется **концентрация распределений** аддитивных функций. Автор изучает, как значения аддитивных функций группируются вокруг своего среднего значения.
- **Ключевые результаты**:
- Получены оценки для функции концентрации $ Q_F(\varepsilon) $.
- Показано, что для широкого класса аддитивных функций распределение значений близко к нормальному.
- **Связь с нормальным распределением**: Работа подчёркивает, что для многих аддитивных функций предельное распределение близко к нормальному, особенно если функция удовлетворяет определённым условиям на простых числах.

В указанных статьях явно не формулируются условия, при которых предельное распределение аддитивной арифметической функции $f(n)$ является нормальным.

[vicvolf]

Теперь о скорости сходимости к нормальному распределению для сильно аддитивных арифметических функций, удовлетворяющих нашим условиям.

### **Основные предположения:**

1. **Поведение $ f(p) $:**
- $ |f(p)| \leq 1 $ для всех простых $ p $.
- $ |f(p)| $ — убывающая функция, то есть $ |f(p)| \geq |f(q)| $ для $ p \leq q $.
- Ряд $ \sum_p \frac{f(p)}{p} $ сходится.

2. **Сильно аддитивная функция $ f(n) $:**
- $ f(n) = \sum_{p|n} f(p) $.

### **Оценка скорости сходимости:**

Скорость сходимости к нормальному распределению зависит от дисперсии $ V_N $ и вклада "больших" отклонений $ f(n) $ от среднего значения $ \mu_N $. Рассмотрим два случая:

#### **1. Случай быстрого убывания $ |f(p)| $:**

Если $ |f(p)| $ убывает быстро (например, $ |f(p)| = O(1/p^{\alpha}) $ для $ \alpha > 1 $), то:

- **Дисперсия $ V_N $:**
- Дисперсия $ V_N $ растет медленно, так как $ |f(p)| $ убывает быстро.
- Оценка дисперсии: $ V_N = O\left( \frac{1}{N} \sum_{n \leq N} f(n)^2 \right) $.

- **Скорость сходимости:**
- В этом случае сходимость к нормальному распределению происходит быстро.
- Оценка скорости сходимости:

$$ \sup_x \left| \frac{1}{N} \cdot \#\{n \leq N : f(n) \leq x\} - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| = O\left( \frac{1}{\sqrt{N}} \right). $$

#### **2. Случай медленного убывания $ |f(p)| $:**

Если $ |f(p)| $ убывает медленно (например, $ |f(p)| = O(1/\log p) $), то:

- **Дисперсия $ V_N $:**
- Дисперсия $ V_N $ растет быстрее, так как $ |f(p)| $ убывает медленно.
- Оценка дисперсии: $ V_N = O\left( \frac{1}{N} \sum_{n \leq N} f(n)^2 \right) $.

- **Скорость сходимости:**
- В этом случае сходимость к нормальному распределению происходит медленнее.
- Оценка скорости сходимости:

$$ \sup_x \left| \frac{1}{N} \cdot \#\{n \leq N : f(n) \leq x\} - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| = O\left( \frac{1}{\log N} \right). $$

### **Общая оценка скорости сходимости:**

Скорость сходимости к нормальному распределению зависит от скорости убывания $ |f(p)| $. Если $ |f(p)| $ убывает быстро (например, $ |f(p)| = O(1/p^{\alpha}) $ для $ \alpha > 1 $), то сходимость происходит со скоростью $ O\left( \frac{1}{\sqrt{N}} \right) $. Если $ |f(p)| $ убывает медленно (например, $ |f(p)| = O(1/\log p) $), то сходимость происходит со скоростью $ O\left( \frac{1}{\log N} \right) $.

[vicvolf]

В последнем сообщении ошибка. Случая 2 (медленной сходимости) нет.
При указанных выше предположениях справедлив только случай 1 (быстрой сходимости). Покажем это.

Для данного случая, когда $ f(n) = \sum_{p \mid n} f(p) $, $ |f(p)| \leq 1 $, $ |f(p)| $ — убывающая функция, и ряд $ \sum_{p} \frac{|f(p)|}{p} $ сходится, можно применить **неравенство Берри–Эссеена** для оценки скорости сходимости распределения $ f(n) $ к нормальному распределению.

### Неравенство Берри–Эссеена
Неравенство Берри–Эссеена оценивает разницу между функцией распределения нормированной суммы случайных величин и стандартной нормальной функцией распределения. В данном случае $ f(n) $ можно рассматривать как сумму независимых случайных величин, соответствующих вкладам простых делителей $ p $.

Пусть:
- $ \mu = \sum_{p} \frac{f(p)}{p} $ — математическое ожидание $ f(n) $,
- $ \sigma^2 = \sum_{p} \frac{f(p)^2}{p} $ — дисперсия $ f(n) $,
- $ F_N(x) $ — функция распределения нормированной суммы $ \frac{f(n) - \mu}{\sigma} $ для $ n \leq N $,
- $ \Phi(x) $ — стандартная нормальная функция распределения.

Тогда неравенство Берри–Эссеена имеет вид:

$$ \sup_{x \in \mathbb{R}} \left| F_N(x) - \Phi(x) \right| \leq \frac{C}{\sigma^3 \sqrt{N}} \sum_{p \leq N} \frac{|f(p)|^3}{p}, $$

где $ C $ — константа.

### Упрощение для данного случая
1. **Ограниченность $ f(p) $**:
Поскольку $ |f(p)| \leq 1 $, то $ |f(p)|^3 \leq |f(p)| $. Поэтому:
$ \sum_{p \leq N} \frac{|f(p)|^3}{p} \leq \sum_{p \leq N} \frac{|f(p)|}{p}. $

2. **Сходимость ряда**:
Ряд $ \sum_{p} \frac{f(p)}{p} $ сходится, поэтому $ \sum_{p \leq N} \frac{|f(p)|}{p} $ ограничен сверху некоторой константой $ C_1 $.

3. **Оценка дисперсии**:
Дисперсия $ \sigma^2 = \sum_{p} \frac{f(p)^2}{p} $ также сходится, так как $ f(p)^2 \leq |f(p)| $.

4. **Итоговая оценка**:
Подставляя в неравенство Берри–Эссеена, получаем:

$$ \sup_{x \in \mathbb{R}} \left| F_N(x) - \Phi(x) \right| \leq \frac{C \cdot C_1}{\sigma^3 \sqrt{N}}. $$

### Интерпретация
Неравенство Берри–Эссеена показывает, что скорость сходимости нормированного распределения $ f(n) $ к стандартному нормальному распределению оценивается как $ O\left(\frac{1}{\sqrt{N}}\right) $. Это означает, что с ростом $ N $ распределение $ f(n) $ быстро приближается к нормальному. Это связано с тем, что в данном случае все моменты сильно аддитивной арифметической функции ограничены, поэтому достигается высокая концентрация распределения, в терминах рассмотренных выше работ.

[vicvolf]

Теперь от сильно аддитивных арифметических функций перейдем к более широкому классу - аддитивных арифметических функций.

### Характеристическая функция
Согласно теореме Эрдёша–Винтнера, если предельное распределение аддитивной арифметической функции $f(n)$ существует и может быть выражено через вклады от каждого простого числа $ p $, то характеристическая функция предельного распределения имеет вид:

$$ \phi(t) = \prod_{p} \left(1 - \frac{1}{p}\right) \cdot \left(1 + \sum_{k=1}^{\infty} p^{-k} e^{it f(p)^k} \right). $$

### Представление как сумма независимых случайных величин
1. **Вклад от каждого простого числа $ p $:**
Для каждого простого числа $ p $ определим случайную величину $ X_p $, которая принимает значение $ f(p)^k $ с вероятностью $ \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $ для $ k = 0, 1, 2, \dots $.
2. **Характеристическая функция для $ X_p $:**
Характеристическая функция для $ X_p $ имеет вид:

$$ \phi_p(t) = \mathbb{E}[e^{itX_p}] = \left(1 - \frac{1}{p}\right) \cdot \left(1 + \sum_{k=1}^{\infty} p^{-k} e^{it f(p)^k} \right). $$

3. **Произведение характеристических функций:**
Характеристическая функция предельного распределения $ \phi(t) $ может быть записана как произведение характеристических функций $ \phi_p(t) $ независимых случайных величин $X_p$ для каждого простого числа $ p $:

$$ \phi(t) = \prod_{p} \phi_p(t). $$

### Итог
Таким образом, характеристическая функция предельного распределения $ \phi(t) $ раскладывается в произведение характеристических функций независимых случайных величин $ X_p $, соответствующих вкладам от каждого простого числа $ p $. Это подтверждает, что если у аддитивной функции $ f(n) $ имеется предельное распределение, то она может быть представлена как сумма независимых случайных величин $X_p$.

Таким образом, в этом случае для аддитивной арифметической функции $f=\sum_p{X_p}$, где $X_p$ - независимые случайные величины.

Поэтому момент $n$ -ого порядка аддитивной арифметической функции $f=\sum_p{X_p}$ равен:
$E[\sum_p{X_p}^n]=\sum_p \sum_{k=0}^{\infty}{\frac{f(p^k)^n}{p^k}(1-1/p)}$.

В частном случае получаем математическое ожидание аддитивной арифметической функции $f=\sum_p{X_p}$ равен:
$E[\sum_p{X_p}]=\sum_p \sum_{k=0}^{\infty}{\frac{f(p^k)}{p^k}(1-1/p)}$.

Дисперсия аддитивной арифметической функции $f=\sum_p{X_p}$ равен:
$D[\sum_p{X_p}]=\sum_p \sum_{k=0}^{\infty}{\frac{f(p^k)^2}{p^k}(1-1/p)}-(\sum_p \sum_{k=0}^{\infty}{\frac{f(p^k)}{p^k}(1-1/p)})^2$.

[vicvolf]

Докажем выполнения теоремы Эрдёша–Винтнера и условия Линдберга для аддитивной арифметической функции $ f $, удовлетворяющей условиям:

1. $ |f(p)| \leq 1 $ для всех простых $ p $,
2. $ |f(p)| $ — убывающая функция,
3. Ряд $ \sum_{p} \frac{|f(p)|}{p} $ сходится,

### 1. Выполнение теоремы Эрдёша–Винтнера

Теорема Эрдёша–Винтнера утверждает, что предельное распределение для аддитивной функции $ f $ существует тогда и только тогда, когда сходятся следующие три ряда:

1. $ \sum_{\substack{p \\ |f(p)| > 1}} \frac{1}{p}, $
2. $ \sum_{\substack{p \\ |f(p)| \leq 1}} \frac{f(p)}{p}, $
3. $ \sum_{\substack{p \\ |f(p)| \leq 1}} \frac{f(p)^2}{p}. $

В нашем случае $ |f(p)| \leq 1 $ для всех простых $ p $, поэтому первый ряд автоматически сходится (так как множество простых $ p $, для которых $ |f(p)| > 1 $, пусто). Остаётся проверить сходимость второго и третьего рядов.

#### Сходимость второго ряда:
Ряд $ \sum_{p} \frac{f(p)}{p} $ сходится абсолютно, так как $ |f(p)| \leq 1 $, и по условию $ \sum_{p} \frac{|f(p)|}{p} $ сходится. Следовательно, второй ряд сходится.

#### Сходимость третьего ряда:
Ряд $ \sum_{p} \frac{f(p)^2}{p} $ также сходится, так как $ |f(p)| \leq 1 $, и $ f(p)^2 \leq |f(p)| $. Поэтому:
$ \sum_{p} \frac{f(p)^2}{p} \leq \sum_{p} \frac{|f(p)|}{p}, $
а последний ряд сходится по условию.

Таким образом, все три ряда сходятся, и по теореме Эрдёша–Винтнера предельное распределение для $ f $ существует.

### 2. Выполнение условия Линдберга

Условие Линдберга требует, чтобы для любого $\epsilon > 0$:

$$ \lim_{N \to \infty} \frac{1}{s_N^2} \sum_{p \leq N} \mathbb{E}\left[ X_p^2 \cdot \mathbb{I}_{\{|X_p| > \epsilon s_N\}} \right] = 0, $$

где:
- $X_p = f(p)$ с вероятностью $\frac{1}{p}$,
- $\mathbb{E}[X_p^2] = \frac{f(p)^2}{p}$,
- $s_N^2 = \sum_{p \leq N} \mathbb{E}[X_p^2] = \sum_{p \leq N} \frac{f(p)^2}{p}$.

#### Оценка $s_N^2$:
По условию, ряд $\sum_p \frac{f(p)^2}{p}$ сходится. Это означает, что $s_N^2$ ограничена сверху некоторой константой $C$, то есть:
$ s_N^2 = \sum_{p \leq N} \frac{f(p)^2}{p} \leq C. $
Таким образом, $s_N^2$ не растёт неограниченно, а стремится к конечному пределу.

#### Проверка условия Линдберга:
Для любого $\epsilon > 0$ и для всех простых $p$, выполняется $|X_p| = |f(p)| \leq 1$. Поскольку $s_N^2$ ограничена, то $\epsilon s_N$ также ограничена. Однако, для достаточно больших $N$, $\epsilon s_N$ может стать больше, чем $|f(p)|$, так как $|f(p)| \leq 1$. Это означает, что для всех $p \leq N$:
$ |X_p| = |f(p)| \leq 1 \leq \epsilon s_N, $
если $\epsilon s_N \geq 1$. Следовательно, индикатор $\mathbb{I}_{\{|X_p| > \epsilon s_N\}}$ равен нулю для всех $p \leq N$, и условие Линдберга выполняется тривиально.

Если $\epsilon s_N < 1$, то $|X_p| = |f(p)| \leq 1$ может быть больше, чем $\epsilon s_N$. Однако, поскольку $s_N^2$ ограничена, то $\epsilon s_N$ также ограничена, и для достаточно больших $N$ это неравенство перестаёт выполняться. Таким образом, для всех $p \leq N$:
$ \mathbb{I}_{\{|X_p| > \epsilon s_N\}} = 0, $
и условие Линдберга выполняется.

### Итог

1. Теорема Эрдёша–Винтнера выполняется, так как все три ряда сходятся.
2. Условие Линдберга выполняется, так как $s_N^2$ ограничена, и $|f(p)| \leq 1$ для всех простых $p$.

Таким образом, для функции $f$, удовлетворяющей условиям задачи, предельное распределение существует, и к нему применима центральная предельная теорема, т.е. предельное распределение является нормальным.

[vicvolf]

Теперь о скорости сходимости аддитивной арифметической функций $f(n)$ к нормальному распределению при следующих условиях:

- $ |f(p)| \leq 1 $ для всех простых чисел $ p $.
- $ |f(p)| $ — убывающая функция.
- Ряд $ \sum_p \frac{|f(p)|}{p} $ сходится.

### **Неравенство Берри-Эссеена:**

Неравенство Берри-Эссеена дает оценку скорости сходимости к нормальному распределению для сумм независимых случайных величин.
Для суммы независимых случайных величин $ X_1, X_2, \dots, X_k $ она утверждает:

$$ \sup_x \left| F_k(x) - \Phi\left( \frac{x - \mu_k}{\sigma_k} \right) \right| \leq \frac{C \rho_k}{\sigma_k^3}, $$

где:
- $ F_k(x) $ — функция распределения (CDF) суммы $ S_k = X_1 + X_2 + \dots + X_k $,
- $ \Phi $ — функция распределения стандартного нормального распределения,
- $ \mu_k $ — математическое ожидание $ S_k $,
- $ \sigma_k^2 $ — дисперсия $ S_k $,
- $ \rho_k = \sum_{i=1}^k E[|X_i - \mu_i|^3] $ — третий абсолютный момент,
- $ C $ — константа (известно, что $ C < 0.4748 $).

### **Применение к аддитивной арифметической функции $ f(n) $:**

1. **Моделирование $ f(n) $ как суммы независимых случайных величин:**
- Рассмотрим $ n $, выбранное равномерно случайно из множества $ \{1, 2, \dots, N\} $.
- Определим $ Y_p = f(p) \cdot I_p(n) $, где $ I_p(n) = 1 $, если $ p $ делит $ n $, и $ I_p(n) = 0 $ иначе.
- Величины $ Y_p $ приближенно независимы для различных простых чисел $ p $.

2. **Математическое ожидание и дисперсия:**
- Математическое ожидание: $ \mu_N = \sum_{p \leq N} \frac{f(p)}{p} $.
- Дисперсия: $ V_N = \sum_{p \leq N} \frac{f(p)^2}{p} \left(1 - \frac{1}{p}\right) \approx \sum_{p \leq N} \frac{f(p)^2}{p} $.

3. **Третий абсолютный момент:**
- $ \rho = \sum_{p \leq N} \frac{|f(p)|^3}{p} $.

### **Оценка скорости сходимости:**

Поскольку ряд $ \sum_p \frac{f(p)^2}{p} $ сходится, дисперсия $ V_N $ и третий момент $ \rho $ сходятся к конечным пределам при $ N \to \infty $. Следовательно, неравенство Берри-Эссеена дает:

$$ \sup_x \left| F_N(x) - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| \leq \frac{C \rho}{V_N^{3/2}}. $$

Так как $ V_N $ и $ \rho $ сходятся к константам, скорость сходимости определяется как $ O\left( \frac{1}{\sqrt{N}} \right). $.

### **Заключение:**

Для аддитивной функции $ f(n)$, при данных условиях, скорость сходимости к нормальному распределению всегда составляет $ O\left( \frac{1}{\sqrt{N}} \right) $, независимо от скорости убывания $ |f(p)| $. Это следует из неравенства Берри-Эссеена, так как дисперсия и третий момент сходятся к конечным пределам.

[vicvolf]

Для аддитивной функции изменим $X_p$ в доказательстве выполнения условия Линдберга.

Докажем выполнения теоремы Эрдёша–Винтнера и условия Линдберга для аддитивной арифметической функции $ f $, удовлетворяющей условиям:

1. $ |f(p)| \leq 1 $ для всех простых $ p $,
2. $ |f(p)| $ — убывающая функция,
3. Ряд $ \sum_{p} \frac{|f(p)|}{p} $ сходится,

### 1. Выполнение теоремы Эрдёша–Винтнера

Теорема Эрдёша–Винтнера утверждает, что предельное распределение для аддитивной функции $ f $ существует тогда и только тогда, когда сходятся следующие три ряда:

1. $ \sum_{\substack{p \\ |f(p)| > 1}} \frac{1}{p}, $
2. $ \sum_{\substack{p \\ |f(p)| \leq 1}} \frac{f(p)}{p}, $
3. $ \sum_{\substack{p \\ |f(p)| \leq 1}} \frac{f(p)^2}{p}. $

В нашем случае $ |f(p)| \leq 1 $ для всех простых $ p $, поэтому первый ряд автоматически сходится (так как множество простых $ p $, для которых $ |f(p)| > 1 $, пусто). Остаётся проверить сходимость второго и третьего рядов.

#### Сходимость второго ряда:
Ряд $ \sum_{p} \frac{f(p)}{p} $ сходится абсолютно, так как $ |f(p)| \leq 1 $, и по условию $ \sum_{p} \frac{|f(p)|}{p} $ сходится. Следовательно, второй ряд сходится.

#### Сходимость третьего ряда:
Ряд $ \sum_{p} \frac{f(p)^2}{p} $ также сходится, так как $ |f(p)| \leq 1 $, и $ f(p)^2 \leq |f(p)| $. Поэтому:
$ \sum_{p} \frac{f(p)^2}{p} \leq \sum_{p} \frac{|f(p)|}{p}, $
а последний ряд сходится по условию.

Таким образом, все три ряда сходятся, и по теореме Эрдёша–Винтнера предельное распределение для $ f $ существует.

### 2. Выполнение условия Линдберга

Условие Линдберга требует, чтобы для любого $ \epsilon > 0 $:

$$ \lim_{N \to \infty} \frac{1}{s_N^2} \sum_{p \leq N} \mathbb{E}\left[ X_p^2 \cdot \mathbb{I}_{\{|X_p| > \epsilon s_N\}} \right] = 0, $$

где:
- $ X_p = f(p)^k $ с вероятностью $ \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $,
- $ \mathbb{E}[X_p^2] = \sum_{k=0}^{\infty} f(p)^{2k} \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $,
- $ s_N^2 = \sum_{p \leq N} \mathbb{E}[X_p^2] $.

#### Оценка $ s_N^2 $:
Поскольку $ |f(p)| \leq 1 $, то $ f(p)^{2k} \leq 1 $ для всех $ k $. Таким образом:
$ \mathbb{E}[X_p^2] \leq \sum_{k=0}^{\infty} \left(1 - \frac{1}{p}\right) \frac{1}{p^k} = \left(1 - \frac{1}{p}\right) \frac{1}{1 - \frac{1}{p}} = 1. $
Следовательно, $ s_N^2 \leq \sum_{p \leq N} 1 $, что ограничено сверху.

#### Проверка условия Линдберга:
Для любого $ \epsilon > 0 $ и для всех простых $ p $, выполняется $ |X_p| = |f(p)^k| \leq 1 $. Поскольку $ s_N^2 $ ограничена, то $ \epsilon s_N $ также ограничена. Однако, для достаточно больших $ N $, $ \epsilon s_N $ может стать больше, чем $ |f(p)^k| $, так как $ |f(p)^k| \leq 1 $. Это означает, что для всех $ p \leq N $:
$ |X_p| = |f(p)^k| \leq 1 \leq \epsilon s_N, $
если $ \epsilon s_N \geq 1 $. Следовательно, индикатор $ \mathbb{I}_{\{|X_p| > \epsilon s_N\}} $ равен нулю для всех $ p \leq N $, и условие Линдберга выполняется тривиально.

Если $ \epsilon s_N < 1 $, то $ |X_p| = |f(p)^k| \leq 1 $ может быть больше, чем $ \epsilon s_N $. Однако, поскольку $ s_N^2 $ ограничена, то $ \epsilon s_N $ также ограничена, и для достаточно больших $ N $ это неравенство перестаёт выполняться. Таким образом, для всех $ p \leq N $:
$ \mathbb{I}_{\{|X_p| > \epsilon s_N\}} = 0, $
и условие Линдберга выполняется.

### Итог

1. Теорема Эрдёша–Винтнера выполняется, так как все три ряда сходятся.
2. Условие Линдберга выполняется, так как $ s_N^2 $ ограничена, и $ |f(p)^k| \leq 1 $ для всех простых $ p $.

Таким образом, для функции $ f $, удовлетворяющей условиям задачи, предельное распределение существует, и к нему применима центральная предельная теорема, т.е. предельное распределение является нормальным.

-- 18.01.2025, 19:10 --
Изменим $Y_p$ в доказательстве о скорости сходимости аддитивной арифметической функции к нормальному распределению с использованием неравенства Берри-Эссена.

Итак о скорости сходимости аддитивной арифметической функций $f(n)$ к нормальному распределению при следующих условиях:

- $ |f(p)| \leq 1 $ для всех простых чисел $ p $.
- $ |f(p)| $ — убывающая функция.
- Ряд $ \sum_p \frac{|f(p)|}{p} $ сходится.

### **Неравенство Берри-Эссеена:**

Неравенство Берри-Эссеена дает оценку скорости сходимости к нормальному распределению для сумм независимых случайных величин.
Для суммы независимых случайных величин $ Y_1, Y_2, \dots, Y_k $ оно утверждает:

$$ \sup_x \left| F_k(x) - \Phi\left( \frac{x - \mu_k}{\sigma_k} \right) \right| \leq \frac{C \rho_k}{\sigma_k^3}, $$

где:
- $ F_k(x) $ — функция распределения (CDF) суммы $ S_k = Y_1 + Y_2 + \dots + Y_k $,
- $ \Phi $ — функция распределения стандартного нормального распределения,
- $ \mu_k $ — математическое ожидание $ S_k $,
- $ \sigma_k^2 $ — дисперсия $ S_k $,
- $ \rho_k = \sum_{i=1}^k E[|Y_i - \mu_i|^3] $ — третий абсолютный момент,
- $ C $ — константа (известно, что $ C < 0.4748 $).

### **Применение к аддитивной арифметической функции $ f(n) $:**

1. **Моделирование $ f(n) $ как суммы независимых случайных величин:**
- Рассмотрим $ n $, выбранное равномерно случайно из множества $ \{1, 2, \dots, N\} $.
- Определим $ Y_p = f(p)^k $ с вероятностью $ \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $ для $ k = 0, 1, 2, \dots $.
- Величины $ Y_p $ независимы для различных простых чисел $ p $, так как $f(n)$ сходится к предельному распределению (показано ранее).

2. **Математическое ожидание и дисперсия:**
- Математическое ожидание:
$ \mu_N = \sum_{p \leq N} \mathbb{E}[Y_p] = \sum_{p \leq N} \sum_{k=0}^{\infty} f(p)^k \left(1 - \frac{1}{p}\right) \frac{1}{p^k}. $
Поскольку $ |f(p)| \leq 1 $, ряд сходится, и:
$ \mathbb{E}[Y_p] = \left(1 - \frac{1}{p}\right) \sum_{k=0}^{\infty} \frac{f(p)^k}{p^k} = \left(1 - \frac{1}{p}\right) \frac{1}{1 - \frac{f(p)}{p}}. $
- Дисперсия:
$ V_N = \sum_{p \leq N} \text{Var}(Y_p) = \sum_{p \leq N} \left( \mathbb{E}[Y_p^2] - (\mathbb{E}[Y_p])^2 \right). $
Поскольку $ |f(p)| \leq 1 $, $ \mathbb{E}[Y_p^2] $ и $ (\mathbb{E}[Y_p])^2 $ ограничены, и $ V_N $ сходится.

3. **Третий абсолютный момент:**
- Третий момент:
$ \rho = \sum_{p \leq N} \mathbb{E}[|Y_p - \mu_p|^3]. $
Поскольку $ |f(p)| \leq 1 $, $ \rho $ также сходится.

### **Оценка скорости сходимости:**

Поскольку ряд $ \sum_p \frac{f(p)^2}{p} $ сходится, дисперсия $ V_N $ и третий момент $ \rho $ сходятся к конечным пределам при $ N \to \infty $. Следовательно, неравенство Берри-Эссеена дает:

$ \sup_x \left| F_N(x) - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| \leq \frac{C \rho}{V_N^{3/2}}. $

Так как $ V_N $ и $ \rho $ сходятся к константам, скорость сходимости определяется как $ O\left( \frac{1}{\sqrt{N}} \right) $.

### **Заключение:**

Для аддитивной функции $ f(n) $, при данных условиях, скорость сходимости к нормальному распределению всегда составляет $ O\left( \frac{1}{\sqrt{N}} \right) $, независимо от скорости убывания $ |f(p)| $. Это следует из неравенства Берри-Эссеена, так как дисперсия и третий момент сходятся к конечным пределам.

[vicvolf]

Исправление

Согласно теореме Эрдёша–Винтнера, если предельное распределение аддитивной арифметической функции $ f(n) $ существует, то характеристическая функция предельного распределения имеет вид:

$$ \phi(t) = \prod_{p} \left(1 - \frac{1}{p}\right) \cdot \left(1 + \sum_{k=1}^{\infty} p^{-k} e^{it f(p^k)} \right). $$

### **Представление как сумма независимых случайных величин**

1. **Вклад от каждого простого числа $ p $:**
Для каждого простого числа $ p $ определим случайную величину $ X_p $, которая принимает значение $ f(p^k) $ с вероятностью $ \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $ для $ k = 0, 1, 2, \dots $.

2. **Характеристическая функция для $ X_p $:**
Характеристическая функция для $ X_p $ имеет вид:
$ \phi_p(t) = \mathbb{E}[e^{itX_p}] = \left(1 - \frac{1}{p}\right) \cdot \left(1 + \sum_{k=1}^{\infty} p^{-k} e^{it f(p^k)} \right). $

3. **Произведение характеристических функций:**
Характеристическая функция предельного распределения $ \phi(t) $ может быть записана как произведение характеристических функций $ \phi_p(t) $ независимых случайных величин $ X_p $ для каждого простого числа $ p $:
$ \phi(t) = \prod_{p} \phi_p(t). $

Таким образом, характеристическая функция предельного распределения $ \phi(t) $ раскладывается в произведение характеристических функций независимых случайных величин $ X_p $, соответствующих вкладам от каждого простого числа $ p $. Это подтверждает, что если у аддитивной функции $ f(n) $ имеется предельное распределение, то она может быть представлена как сумма независимых случайных величин $ X_p $.

### **Моменты аддитивной арифметической функции**

Момент $ n $-го порядка аддитивной арифметической функции $ f = \sum_p X_p $ равен:

$ \mathbb{E}\left[\left(\sum_p X_p\right)^n\right] = \sum_p \sum_{k=0}^{\infty} \frac{f(p^k)^n}{p^k} \left(1 - \frac{1}{p}\right). $

В частном случае математическое ожидание аддитивной арифметической функции $ f = \sum_p X_p $ равно:

$ \mathbb{E}\left[\sum_p X_p\right] = \sum_p \sum_{k=0}^{\infty} \frac{f(p^k)}{p^k} \left(1 - \frac{1}{p}\right). $

Дисперсия аддитивной арифметической функции $ f = \sum_p X_p $, где $ X_p $ — независимые случайные величины, определяется как:

$ \text{Var}(f) = \sum_p \left(1 - \frac{1}{p}\right) \sum_{k=0}^\infty \frac{f(p^k)^2}{p^k} -(\sum_p \left(1 - \frac{1}{p}\right) \sum_{k=0}^\infty \frac{f(p^k)}{p^k})^2 $.

[vicvolf]

Исправление

### **Доказательство выполнения теоремы Эрдёша–Винтнера и условия Линдберга для аддитивной арифметической функции $ f $**

Рассмотрим аддитивную арифметическую функцию $ f $, удовлетворяющую следующим условиям:

1. $ |f(p)| \leq 1 $ для всех простых чисел $ p $,
2. $ |f(p)| $ — убывающая функция,
3. Ряд $ \sum_{p} \frac{|f(p)|}{p} $ сходится.

### **1. Выполнение теоремы Эрдёша–Винтнера**

Теорема Эрдёша–Винтнера утверждает, что предельное распределение для аддитивной функции $ f $ существует тогда и только тогда, когда сходятся следующие три ряда:

1. $ \sum_{\substack{p \\ |f(p)| > 1}} \frac{1}{p}, $
2. $ \sum_{\substack{p \\ |f(p)| \leq 1}} \frac{f(p)}{p}, $
3. $ \sum_{\substack{p \\ |f(p)| \leq 1}} \frac{f(p)^2}{p}. $

В нашем случае $ |f(p)| \leq 1 $ для всех простых чисел $ p $, поэтому первый ряд автоматически сходится (так как множество простых чисел $ p $, для которых $ |f(p)| > 1 $, пусто). Остаётся проверить сходимость второго и третьего рядов.

Сходимость второго ряда:
Ряд $ \sum_{p} \frac{f(p)}{p} $ сходится абсолютно, так как $ |f(p)| \leq 1 $, и по условию $ \sum_{p} \frac{|f(p)|}{p} $ сходится. Следовательно, второй ряд сходится.

Сходимость третьего ряда:
Ряд $ \sum_{p} \frac{f(p)^2}{p} $ также сходится, так как $ |f(p)| \leq 1 $, и $ f(p)^2 \leq |f(p)| $. Поэтому:
$ \sum_{p} \frac{f(p)^2}{p} \leq \sum_{p} \frac{|f(p)|}{p}, $
а последний ряд сходится по условию.

Таким образом, все три ряда сходятся, и по теореме Эрдёша–Винтнера предельное распределение для $ f $ существует.

### **2. Выполнение условия Линдберга**

Условие Линдберга требует, чтобы для любого $ \epsilon > 0 $:

$$ \lim_{N \to \infty} \frac{1}{s_N^2} \sum_{p \leq N} \mathbb{E}\left[ X_p^2 \cdot \mathbb{I}_{\{|X_p| > \epsilon s_N\}} \right] = 0, $$

где:
- $ X_p = f(p^k) $ с вероятностью $ \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $,
- $ \mathbb{E}[X_p^2] = \sum_{k=0}^{\infty} f(p^k)^2 \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $,
- $ s_N^2 = \sum_{p \leq N} \mathbb{E}[X_p^2] $.

#### Проверка условия Линдберга:
Для любого $ \epsilon > 0 $ и для всех простых чисел $ p $, выполняется $ |X_p| = |f(p^k)| \leq 1 $. Поскольку $ s_N^2 $ ограничена, то $ \epsilon s_N $ также ограничена. Однако, для достаточно больших $ N $, $ \epsilon s_N $ может стать больше, чем $ |f(p^k)| $, так как $ |f(p^k)| \leq 1 $. Это означает, что для всех $ p \leq N $:
$ |X_p| = |f(p^k)| \leq 1 \leq \epsilon s_N, $
если $ \epsilon s_N \geq 1 $. Следовательно, индикатор $ \mathbb{I}_{\{|X_p| > \epsilon s_N\}} $ равен нулю для всех $ p \leq N $, и условие Линдберга выполняется тривиально.

Если $ \epsilon s_N < 1 $, то $ |X_p| = |f(p^k)| \leq 1 $ может быть больше, чем $ \epsilon s_N $. Однако, поскольку $ s_N^2 $ ограничена, то $ \epsilon s_N $ также ограничена, и для достаточно больших $ N $ это неравенство перестаёт выполняться. Таким образом, для всех $ p \leq N $:
$ \mathbb{I}_{\{|X_p| > \epsilon s_N\}} = 0, $
и условие Линдберга выполняется.

### **Итог**

1. Теорема Эрдёша–Винтнера выполняется, так как все три ряда сходятся.
2. Условие Линдберга выполняется, так как $ s_N^2 $ ограничена, и $ |f(p^k)| \leq 1 $ для всех простых чисел $ p $.

Таким образом, для функции $ f $, удовлетворяющей условиям задачи, предельное распределение существует, и к нему применима центральная предельная теорема, т.е. предельное распределение является нормальным.

Теперь рассмотрим скорость сходимости аддитивной арифметической функции $ f(n) $ к нормальному распределению с использованием неравенства Берри-Эссеена.

#### **Неравенство Берри-Эссеена:**

Неравенство Берри-Эссеена даёт оценку скорости сходимости к нормальному распределению для сумм независимых случайных величин. Для суммы независимых случайных величин $ X_1, X_2, \dots, X_k $ оно утверждает:

$$ \sup_x \left| F_k(x) - \Phi\left( \frac{x - \mu_k}{\sigma_k} \right) \right| \leq \frac{C \rho_k}{\sigma_k^3}, $$

где:
- $ F_k(x) $ — функция распределения (CDF) суммы $ S_k = X_1 + X_2 + \dots + X_k $,
- $ \Phi $ — функция распределения стандартного нормального распределения,
- $ \mu_k $ — математическое ожидание $ S_k $,
- $ \sigma_k^2 $ — дисперсия $ S_k $,
- $ \rho_k = \sum_{i=1}^k \mathbb{E}[|X_i - \mu_i|^3] $ — третий абсолютный момент,
- $ C $ — константа (известно, что $ C < 0.4748 $).

#### **Применение к аддитивной арифметической функции $ f(n) $:**

1. **Моделирование $ f(n) $ как суммы независимых случайных величин:**
- Рассмотрим $ n $, выбранное равномерно случайно из множества $ \{1, 2, \dots, N\} $.
- Определим $ X_p = f(p^k) $ с вероятностью $ \left(1 - \frac{1}{p}\right) \frac{1}{p^k} $ для $ k = 0, 1, 2, \dots $.
- Величины $ X_p $ независимы для различных простых чисел $ p $, так как $ f(n) $ сходится к предельному распределению (показано ранее).

2. **Математическое ожидание и дисперсия:**
- Математическое ожидание:
$ \mu_N = \sum_{p \leq N} \mathbb{E}[X_p] = \sum_{p \leq N} \sum_{k=0}^{\infty} f(p^k) \left(1 - \frac{1}{p}\right) \frac{1}{p^k}. $
- Дисперсия:
$ V_N = \sum_{p \leq N} \text{Var}(X_p) = \sum_{p \leq N} \left( \mathbb{E}[X_p^2] - (\mathbb{E}[X_p])^2 \right). $

3. **Третий абсолютный момент:**
- Третий момент:
$ \rho = \sum_{p \leq N} \mathbb{E}[|X_p - \mu_p|^3]. $

#### **Оценка скорости сходимости:**

Поскольку ряд $ \sum_p \frac{f(p)^2}{p} $ сходится, дисперсия $ V_N $ и третий момент $ \rho $ сходятся к конечным пределам при $ N \to \infty $. Следовательно, неравенство Берри-Эссеена даёт:

$ \sup_x \left| F_N(x) - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| \leq \frac{C \rho}{V_N^{3/2}}. $

Так как $ V_N $ и $ \rho $ сходятся к константам, скорость сходимости определяется как $ O\left( \frac{1}{\sqrt{N}} \right) $.

### **Заключение:**

Для аддитивной функции $ f(n) $, при данных условиях, скорость сходимости к нормальному распределению всегда составляет $ O\left( \frac{1}{\sqrt{N}} \right) $, независимо от скорости убывания $ |f(p)| $. Это следует из неравенства Берри-Эссеена, так как дисперсия и третий момент сходятся к конечным пределам.

[vicvolf]

В формулах скорости сходимости фигурирует $N$. Это количество ненулевых слагаемых в сумме, представляющей предельное распределение аддитивной арифметической функции. $N$ растёт асимптотически как $ \log \log x $ при $ x $, стремящемся к бесконечности. Этот темп роста вытекает из того, что ожидаемое количество ненулевых слагаемых, соответствующих простым числам $ p \leq x $, приблизительно равно $ \sum_{p \leq x} \frac{1}{p} $, что асимптотически ведёт себя как $ \log \log x $. Этот результат является стандартным в аналитической теории чисел и подтверждается интегральным тестом на сходимость и теоремой о распределении простых чисел. Таким образом, количество ненулевых слагаемых увеличивается очень медленно, в соответствии с $ \log \log x $, при увеличении $ x $.

Количество ненулевых слагаемых в сумме, представляющей предельное распределение сильно аддитивной арифметической функции $f(n)=\sum_{p|n}{f(p)}$, растёт асимптотически как $ \log \log n $ при $ n $, стремящемся к бесконечности. Этот рост аналогичен поведению, наблюдаемому для общих аддитивных функций. Обоснование заключается в том, что для сильно аддитивных функций значение на степенях простых чисел совпадает со значением на самих простых числах, а количество различных простых делителей числа $ n $, обозначаемое $ \omega(n) $, имеет средний порядок $ \log \log n $. Таким образом, количество ненулевых слагаемых в сумме, соответствующих различным простым делителям, растёт в соответствии с $ \log \log n $.

[vicvolf]

В качестве примера рассмотрим аддитивную арифметическую функцию $ f(n) = \ln\left(\frac{\sigma(n)}{n}\right) $, где $ \sigma(n) $ — сумма делителей числа $ n $. Мы проведём анализ этой функции, начиная с проверки условий, выполнения теоремы Эрдёша–Винтнера, условия Линдберга и оценки скорости сходимости к нормальному распределению.

### **1. Проверка условий:**

#### **1.1. Проверка $ |f(p)| \leq 1 $:**
Для простого числа $ p $:
$ f(p) = \ln\left(\frac{p + 1}{p}\right) = \ln\left(1 + \frac{1}{p}\right). $
Так как $ \frac{1}{p} \leq \frac{1}{2} $ для $ p \geq 2 $, то:
$ |f(p)| = \ln\left(1 + \frac{1}{p}\right) \leq \ln\left(1 + \frac{1}{2}\right) = \ln\left(\frac{3}{2}\right) \approx 0.405 < 1. $
Таким образом, $ |f(p)| \leq 1 $ для всех простых $ p $.

#### **1.2. Проверка убывания $ |f(p)| $:**
Функция $ f(p) = \ln\left(1 + \frac{1}{p}\right) $ убывает с ростом $ p $, так как $ \frac{1}{p} $ убывает, а логарифм — монотонно возрастающая функция. Следовательно, $ |f(p)| $ — убывающая функция.

#### **1.3. Проверка сходимости ряда $ \sum_p \frac{f(p)}{p} $:**
Для больших $ p $:
$ f(p) = \ln\left(1 + \frac{1}{p}\right) \approx \frac{1}{p} - \frac{1}{2p^2} + O\left(\frac{1}{p^3}\right). $
Тогда:
$ \frac{f(p)}{p} \approx \frac{1}{p^2} - \frac{1}{2p^3} + O\left(\frac{1}{p^4}\right). $
Ряд $ \sum_p \frac{1}{p^2} $ сходится, а остальные члены ряда убывают быстрее. Следовательно, ряд $ \sum_p \frac{f(p)}{p} $ сходится.

### **2. Выполнение теоремы Эрдёша–Винтнера:**

Теорема Эрдёша–Винтнера утверждает, что предельное распределение для аддитивной функции $ f(n) $ существует, если сходятся следующие три ряда:

1. $ \sum_{p: |f(p)| > 1} \frac{1}{p} $,
2. $ \sum_{p: |f(p)| \leq 1} \frac{f(p)}{p} $,
3. $ \sum_{p: |f(p)| \leq 1} \frac{f(p)^2}{p} $.

#### **2.1. Проверка рядов:**
1. Первый ряд $ \sum_{p: |f(p)| > 1} \frac{1}{p} $ пуст, так как $ |f(p)| \leq 1 $ для всех простых $ p $. Следовательно, он сходится.
2. Второй ряд $ \sum_{p: |f(p)| \leq 1} \frac{f(p)}{p} $ совпадает с $ \sum_p \frac{f(p)}{p} $, который сходится по условию.
3. Третий ряд $ \sum_{p: |f(p)| \leq 1} \frac{f(p)^2}{p} $ также сходится, так как $ f(p)^2 \leq |f(p)| $, и ряд $ \sum_p \frac{f(p)}{p} $ сходится.

Таким образом, все три ряда сходятся, и по теореме Эрдёша–Винтнера предельное распределение для $ f(n) $ существует.

### **3. Выполнение условия Линдберга:**

Условие Линдберга требует, чтобы для любого $ \epsilon > 0 $:

$$ \lim_{N \to \infty} \frac{1}{s_N^2} \sum_{p \leq N} \mathbb{E}\left[ X_p^2 \cdot \mathbb{I}_{\{|X_p| > \epsilon s_N\}} \right] = 0, $$

где:
- $ X_p $ — независимые случайные величины, соответствующие вкладам от простых чисел $ p $,
- $ s_N^2 = \sum_{p \leq N} \mathbb{E}[X_p^2] $ — сумма дисперсий.

#### **3.1. Определение $ X_p $:**
Для каждого простого числа $ p $ определим случайную величину $ X_p $, которая принимает значение $ f(p^\nu) $ с вероятностью $ (1 - 1/p) p^{-\nu} $ для $ \nu \geq 0 $. Таким образом:

$$ X_p = \begin{cases} f(p^\nu) & \text{с вероятностью } (1 - 1/p) p^{-\nu}, \quad \nu \geq 0, \\ 0 & \text{с вероятностью } 1 - \sum_{\nu=1}^\infty (1 - 1/p) p^{-\nu}. \end{cases} $$

#### **3.2. Оценка $ s_N^2 $:**
Для $ X_p $:
$ \mathbb{E}[X_p^2] = \sum_{\nu=0}^\infty f(p^\nu)^2 \cdot (1 - 1/p) p^{-\nu}. $
Для $ f(p^\nu) = \ln\left(\frac{\sigma(p^\nu)}{p^\nu}\right) $, где $ \sigma(p^\nu) = 1 + p + p^2 + \dots + p^\nu $, получаем:
$ f(p^\nu) = \ln\left(\frac{p^{\nu+1} - 1}{p^\nu (p - 1)}\right). $
Для больших $ \nu $ это выражение стремится к $ \ln\left(\frac{p}{p - 1}\right) $. Тогда:
$ \mathbb{E}[X_p^2] \approx \left(\ln\left(\frac{p}{p - 1}\right)\right)^2 \cdot \frac{1 - 1/p}{p}. $
Сумма дисперсий:
$ s_N^2 = \sum_{p \leq N} \mathbb{E}[X_p^2] \approx \sum_{p \leq N} \left(\ln\left(\frac{p}{p - 1}\right)\right)^2 \cdot \frac{1 - 1/p}{p}. $
Так как $ \ln\left(\frac{p}{p - 1}\right) \approx \frac{1}{p} $ для больших $ p $, то:
$ s_N^2 \approx \sum_{p \leq N} \frac{1}{p^3}. $
Этот ряд сходится, поэтому $ s_N^2 $ стремится к конечному пределу $ s^2 $.

#### **3.3. Проверка условия Линдберга:**
Для любого $ \epsilon > 0 $ и достаточно больших $ N $, выполняется:
$ |X_p| \leq \ln\left(\frac{p}{p - 1}\right) \ll \epsilon s_N, $
так как $ s_N $ стремится к конечному пределу. Следовательно, $ \mathbb{I}_{\{|X_p| > \epsilon s_N\}} = 0 $ для всех $ p \leq N $, и условие Линдберга выполняется.

### **4. Скорость сходимости к нормальному распределению:**

Скорость сходимости к нормальному распределению оценивается с помощью неравенства Берри–Эссена:

$$ \sup_x \left| \frac{1}{N} \cdot \#\{n \leq N : f(n) \leq x\} - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| \leq C \cdot \frac{\rho_N}{s_N^3}, $$

где:
- $ \mu_N = \mathbb{E}[Z_{f,N}] $,
- $ V_N = \text{Var}[Z_{f,N}] $,
- $ \rho_N = \sum_{p \leq N} \mathbb{E}[|X_p|^3] $.

#### **4.1. Оценка $ \rho_N $:**
Для $ f(p^\nu) \approx \ln\left(\frac{p}{p - 1}\right) $:
$ \mathbb{E}[|X_p|^3] \approx \left|\ln\left(\frac{p}{p - 1}\right)\right|^3 \cdot \frac{1 - 1/p}{p}. $
Сумма:
$ \rho_N = \sum_{p \leq N} \mathbb{E}[|X_p|^3] \approx \sum_{p \leq N} \frac{1}{p^4}. $
Этот ряд сходится, поэтому $ \rho_N $ стремится к конечному пределу $ \rho $.

#### **4.2. Скорость сходимости:**
Поскольку $ s_N^2 $ и $ \rho_N $ стремятся к конечным пределам, скорость сходимости определяется стандартными результатами центральной предельной теоремы:

$$ \sup_x \left| \frac{1}{N} \cdot \#\{n \leq N : f(n) \leq x\} - \Phi\left( \frac{x - \mu_N}{\sqrt{V_N}} \right) \right| = O\left( \frac{1}{\sqrt{N}} \right). $$

### **Итоговый вывод:**

1. **Условия выполнены:**
- $ |f(p)| \leq 1 $ для всех простых $ p $,
- $ |f(p)| $ — убывающая функция,
- Ряд $ \sum_p \frac{f(p)}{p} $ сходится.

2. **Теорема Эрдёша–Винтнера применима:**
- Предельное распределение для $ f(n) $ существует.

3. **Условие Линдберга выполняется:**
- К $ f(n) $ применима центральная предельная теорема.

4. **Скорость сходимости:**
Таким образом, функция $ f(n) = \ln\left(\frac{\sigma(n)}{n}\right) $ удовлетворяет всем условиям и сходится к нормальному распределению со скоростью $ O\left( \frac{1}{\sqrt{N}} \right) $.
При $n \leq x$ скорость сходимости к нормальному распределению $ O\left( \frac{1}{\sqrt{\ln\ln(x)}} \right) $.

[vicvolf]

Где $Z_{f,N}=\sum_{p \leq N}{X_p}$.